Виды систем эконометрических уравнений (СЭУ)

Объектом статистического изучения в социальных науках являются сложные системы. Система эконометрических уравнений включает в себя 1 или несколько уравнений регрессии и может включать в себя также выражения, называемые тождествами. Обычно в систему включаются уравнения линейной регрессии и тождества (- это функция, отражающая функцион.связь показателей, не содержащая независ.параметров) в линейной форме.

Если в систему входит 1 уравнение регрессии, то оно всегда доп-но тождествами, а если неск-ко, то тождество необязательно.

Совокупность выражений, входящих в СЭУ отражает комплекс взаимосвязей к-го-то эконом. Явления. Поэтому систему называют структурной формой модели.

В рамках СЭУ вводится новая классификация переменных (экзогенные, эндогенные и лаговые переменные)

Система уравнений в эконометрических исследованиях может быть построена по-разному.

1. Самая простая – система независимых уравнений, когда каждая зависимая переменная у рассматривается как функция одного и того же набора факторов х:

Набор факторов x_i в каждом уравнении может варьироваться. Например, модель вида

Также является системой независимых уравнений с отличием в том, что в ней набор факторов видоизменяется в уравнениях, входящих в систему. Отсутствие одного их факторов может объясняться нецелесообразностью включения его в модель, несущественностью его воздействия на результативный признак и др. Каждое уравнение такой системы может рассматриваться самостоятельно. Для нахождения его параметров используется метод наименьших квадратов.

2. Система рекурсивных уравнений – система, когда зависимая переменная у одного уравнения выступает в качестве фактора х в другом уравнении. В этом случае последующий результат зависит от всех факторов и предыдущих результатов:

В данной системе зависимая переменная у включает в каждое последующее уравнение в качестве факторов все зависимые переменные предшествующих уравнений наряду с набором собственно факторов х. Как и в предшествующей модели уравнение может рассматриваться самостоятельно, и его параметры определяются методом наименьших квадратов. В этой сис-ме уравнение можно упорядочить, т.о, чтобы рез-т текущего уравнения входил в качестве факторов во все последующие уравнения.

Система совместных или одновременных уравнений (система взаимозависимых переменных) – наибольшее распространение в эконометрических исследованиях. В ней одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других – в правую часть системы:

В системе одни и те же переменные у рассматриваются как зависимые в одних уравнениях и как независимые в других. В эконометрике эта модель также называется структурной формой модели. В отличие от предыдущих систем каждое уравнение данной модели не может рассматриваться самостоятельно, и для нахождения его параметров МНК неприменим. Используются специальные приемы оценивания (например, с помощью матрицы параметров).

В системе одноврем.уравнений каждый рез-т (эндогенная переменная) зависит от рез-в др.уравнений.различают СОУ в полной и неполной форме

54. Структурная форма модели: состав, виды переменных.

Исходная система (модель), которая отражает реальные связи между показателями, называется структурной формой модели (СФМ).

СФМ содержит эндогенные и экзогенные переменные.

Переменные, которые являются только факторами во всех уравнениях модели, называются экзогенными (х₁,х₂).

Переменные, кот1орые хотя бы в одном из уравнений системы являются результатом, называются эндогенными (у₁,у₂).

Простейшая структурная форма модели имеет вид:

Классификация переменных на эндогенные и экзогенные зависит от теоретической концепции принятой модели. Экономические переменные могут выступать в одних моделях как эндогенные, а в других – как экзогенные. Внеэкономические переменные (например, климатические условия) входят в систему как экзогенные переменные.

В качестве экзогенных переменных могут рассматриваться значения эндогенных переменных за предшествующий период времени – это лаговые переменные. Так, например, потребление текущего года (у_t) может зависеть не только от ряда экономических факторов, но и от уровня потребления в предыдущем году (у_t_-1).

Структурная форма модели позволяет увидеть влияние изменений любой экзогенной переменной на значения эндогенной переменной. Структурная форма модели содержит в правой части при эндогенных и экзогенных переменных коэффициенты b_i (коэффициент при эндогенной) и a_j (при экзогенной), которые называются структурные коэффициенты модели. Все переменные в модели выражены в отклонениях от среднего уровня, т.е. под x подразумевается , а под у – соответственно . Поэтому свободный член в каждом уравнении отсутствует. Использование МНК для оценивания структурных коэффициентов модели дает, как принято считать в теории, смещенные и несостоятельные оценки. Поэтому обычно для определения структурных коэффициентов модели структурная форма модели преобразуется в приведенную форму модели.

55. Приведенная форма модели: структура, предназначение, связь с приведенной формой.

Так как использоьвание МНК для оценивания структурных коэффициентов модели дает, как принято считать в теории, смещенные и несостоятельные оценки. Поэтому обычно для определения структурных коэффициентов модели структурная форма модели преобразуется в приведенную форму модели.

Приведенная форма модели представляет собой систему линейных функций эндогенных переменных от экзогенных:

Где - коэффициенты приведенной формы модели.

По виду приведенная форма ничем не отличается от системы независимых уравнений, параметры которой оцениваются традиционным способом МНК. Применяя МНК, можно оценить , а затем оценить значения эндогенных переменных через экзогенные.

Коэффициенты приведенной формы модели представляют собой нелинейные функции коэффициентов структурной формы модели. Коэффициенты приведенной функции выражаются из модели структурной.

Так, например, структурная модель имеет вид:

Приведенная форма модели имеет вид:

У₂из первого уравнения структурной формы можно выразить как:

. Тогда система одновременных уравнений будет:

Отсюда имеем равенство:

- =

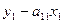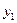Таким образом, мы представили первое уравнение структурной формы модели в виде уравнения формы модели:

Т.е. мы выразили коэффициенты приведенной формы уравнения через соотношения коэффициентов структурной формы:

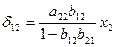
Аналогично доказываем связь коэффициентов приведенной формы модели второго уравнения с коэффициентами структурной модели:

Приведенная форма модели хотя и позволяет получить значения эндогенной переменной через значения экзогенных переменных, аналитически уступает структурной форме модели, так как в ней нет оценки взаимосвязи между эндогенными переменными.