В этой модели предполагается, что связь между показателями является корреляционной. Результат y представляет собой совокупность случайных величин. Для каждого значения фактора х своя случ. величина.
Ряд требований:
1) случ. величина yi распределена по нормальному закону (мода, медиана, мат. ожидание. Дисперсии случ. величин yi и yj одинаковы. Случ. величны независимы для любых ij)
2) фактор х предполагается неслуч. величиной. Если их несколько в модели, то они независимы друг от друга).
3) Объем наблюдений, необходимый для оценки параметров регрессии, должен быть в 6-10 раз больше кол-ва параметров ур-ия без учета своб. члена а.
4) Выровненные значения результата y^ лежат на прямой линии.
Уравнение регрессии в стандартизированном масштабе.
Относительный показатель силы связи – только для множественной линейной регрессии – стандартизированный коэффициэнт регрессии. Предположим, что была проведена операция стандартизации исходных переменных (x,y).
y-y¯/σy=ty Операция стандартизации по Y
y¯=112,6 txр=xр-xр¯/σxр
σy=57,2
tx1=x1-x1¯/σx1 tx2=x2-x2¯/σx2
Для этих новых стандртизированных переменныхможно построить уравнение регрессии
ty=α+β1tx1+β2tx2...βрtxp+δ
α=0, всегда (свойство стандартизированных переменных)
ty=β1tx1+β2tx2...βрtxp+δ – уравнение в стандартизированной форме или стандартизированном масштабе, а исходное – в натуральной форме.
Параметры β1, β2, βр называются стандартизированными коэффициэнтами регрессии. Их можно найти методом наименьших квадратов – это трудоемко. 2 способ – βi=bi*σxi/σy
12. Понятие «статистическая значимость» параметров уравнения регрессии.
В эконометрике все исходные данные рассматриваются как выборочные => можно предположить, что если бы была возможность повторять одно и то же статистическое наблюдение, то полученные данные различались бы друг от друга и отличались бы все показатели по ним рассчитанные.
Опыт 1. Усреднение b=(приближенно)0
Y^=a1+b1x
R²1, b1>0
Опыт 2.
Y^=a2+b2x
R²2, b2>0
Опыт 3.
Y^=a3+b3x
b3<0
Если много экспериментов, то могут быть противоречивые результаты почти по всем коэффициентам регрессии приблизительно равным 0 в среднем. Если такой исход возможен, то говорят, что коэффициент регрессии незначителен.
Параметр называется незначительным, если с большой долей вероятности его величина в генеральной совокупности = 0.
Значимость уравнения регрессии –само уравнение регрессии – тождество чисел.
Незначимость ур-я регрессии означает, что все параметры при факторах одновременно с высокой долей вероятности м.б. равны «0» в ген.сов-ти. Незначимость ур-я регрессии означает также незначимость коэф.детерминации, т.е его равенство «0» с высокой степенью вероятности в гень сов-ти.
Значимость параметров -означает их отличие от 0 с высокой степенью вероятности, а параметра – все параметры при факторе одновременно не = 0. Для того, чтобы оценить значимость параметров и парного линейного коэффициента корреляции, используют критерий Стьюдента (t-критерий).
Для оценки значимости ур-я регрессии в целом используется критерий Фишера.
13. Понятие «статистическая значимость» уравнения регрессии в целом.
В эконометрике все исходные данные рассматриваются как выборочные, значит, можно предположить, что при повторе статистического наблюдения полученные данные отличались бы друг от друга, а, значит, отличались бы и показатели по ним рассчитанные.
Если много наблюдений, могут быть противоречивые результаты и коэффициент регрессии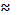 
0, если такой исход возможен, то говорят что коэффициент регрессии незначим.
Значимость уравнения регрессии: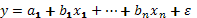 
Незначимость уравнения регрессии означает, что все параметры при факторах одновременно с высокой долей вероятности могут быть равны 0.
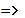
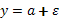или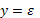 
Незначимость уравнения регрессии, означает незначимость коэффициента детерминации, то есть его равенство 0 с высокой степенью вероятности в генеральной совокупности.
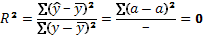
Уравнение значимо если все параметры при факторах одновременно не равны 0.
Значимость уравнения говорит о том, что все факторы в уравнении оказывают влияние на результат.
Для оценки значимости уравнения регрессии в целом используют критерий Фишера или F-критерий.
Критерий Стьюдента.
Используется для оценки значимости параметров уравнения регрессии.
Алгоритм оценки значимости по критерию Стьюдента:
1. Рассчитывается средняя ошибка оцениваемого параметра (или стандартная ошибка) -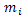 
2. По таблице находят табличное значение t-критерия (при 
); число степеней свободы = n-m-1, где n- число наблюдений, m- число факторов.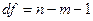 
- это число степеней свободы, на пересечении альфа и df находят t- табличное
3. Фактическое значение t-критерия: 
, т.е. параметр делим на ошибку параметра
4. Сравнивается фактическое и табличное значение t-критерия, если tфакт> 
, то, говорят, что параметр значим с вероятностью 1-α, при этом tфактич. Берется по модулю!
ИЛИ:
5. после пункта 2: Находим границы доверительного интервала для оценки параметра:
, b- параметр
Этот доверительный интервал характеризует значения оцениваемого параметра, которые он может принимать в различных опытах с высокой долей вероятности.
Длят того чтобы параметр был значим, необходимо,чтобы 0 не входил в доверительный интервал, если входит то говорим что параметр незначим в вероятностью 1-α, если не входит, то параметр значим с вероятностью 1-α.
Формула средней ошибки параметра зависит от того какой параметр оценивается. Общая для всех параметров уравнения регрессии формула:
Где, i=0,1,2…p;
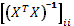- диагональный элемент с N ii матрицы 
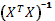, причем i=0,1,2…p
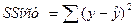
Стандартная ошибка регрессии: 
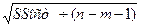
В большинстве случаев приведенную формулу можно упростить, если есть парное линейное уравнение регрессии, то ошибка рассчитывается:
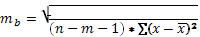в числителе SSост.
А для свободного члена:
Для множественной регрессии формула ошибки одного из коэффициентов регрессии:
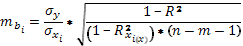
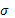- СКО
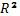- коэффициент детерминации по всему уравнению
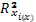- коэффициент детерминации для уравнения регрессии в котором в качестве результатирующего признака входит xi, a в качестве признака остальные факторы входящие в уравнение регрессии.
= 
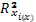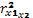
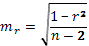- ошибка парного лин.коэф.корреляции
