Стандартная ошибка коэффициента регрессии

Для оценки существенности коэффициента регрессии его ве­личина сравнивается с

его стандартной ошибкой, т. е. определяется фактическое значение t-критерия

Стьюдентa: которое

затем сравнивается с табличным значением при определенном уровне значимости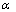

и числе степеней свободы (n- 2).

Стандартная ошибка параметра а:

Значимость линейного коэффициента корреляции проверя­ется на основе величины

ошибки коэффициента корреляции т_r:

Общая дисперсия признака х:

Коэф. регрессии Его

величина показывает ср. изменение результата с изменением фактора на 1 ед.

Ошибка аппроксимации: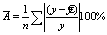

16. Оценка значимости параметров уравнения множественной регрессии

Множественная регрессия-это уравнение связи с несколькими независимыми переменными

Y = b₀ + b₁x_i1 +... + b_jx_ij +... + b_kx_ik + e_i

где e_i - случайные ошибки наблюдения, независимые между собой, имеют нулевую среднюю и дисперсию s.

Экономический смысл параметров множественной регрессии
Коэффициент множественной регрессии b_j показывает, на какую величину в среднем изменится результативный признак Y, если переменную X_j увеличить на единицу измерения, т. е. является нормативным коэффициентом.

Матричная запись множественной линейной модели регрессионного анализа:

Y = Xb + e

Модель множественной регрессии вида Y = b₀ + b₁X₁ + b₂X₂;

Для оценки параметров уравнения множественной регрессии применяют метод наименьших квадратов.

 

Как и в случае множественной регрессии, статистическая значимость коэффициентов множественной регрессии с m объясняющими переменными проверяется на основе t-статистики:

имеющей в данном случае распределение Стьюдента с числом степеней свободы v = n- m-1. При требуемом уровне значимости наблюдаемое значение t-статистики сравнивается с критической точной 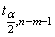распределения Стьюдента.
В случае, если 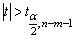, то статистическая значимость соответствующего коэффициента множественной регрессии подтверждается. Это означает, что фактор Xj линейно связан с зависимой переменной Y. Если же установлен факт незначимости коэффициента b_j, то рекомендуется исключить из уравнения переменную Xj. Это не приведет к существенной потере качества модели, но сделает ее более конкретной.

 

 

Формула средней ошибки параметра зависит от какого параметра оценивается. Общая для всех параметров уравнения регрессии формула выглядит следующим образом:

 

Mbi=квадратный корень из SSост./n-m-1 * [X в степени T * X] в минус первой степени) ii

SSост. = E(y-y с домиком) в квадрате

n – число наблюдений

m – количество параметров без свободного члена.

 

([X в степени T * X] в минус первой степени)ii - ii – диагональный элемент с номером ii матрицы ([X в степени T * X] в минус первой степени), причём y = a+b1x1+ … + bpxp + E, i=0,1,2…p

 

Mbo=Ma

 

0 1 2

0 (0)

1 ()

2 ()

3 ()

 

Квадратный корень из SSост.\n-m-1 – стандартная ошибка регрессии

 

В большинстве случаев приведённую формулу ошибки можно упростить, в частности, если имеется парное линейное уравнение регрессии, то ошибка коэффициента регрессии рассчитывается по формуле:

 

Mb = квадратный корень из SSост.\ (n-m-1) * E (x – x c штрихом) в квадрате

 

Ma = квадратный корень из SSост. * Ex в квадрате\ (n-m-1) * E (x – x с штрихом) в квадрате * n

 

y=a+b1x1+…+bpxp+ E

 

Mbi= Gy/Gx * квадратный корень из 1-R в квадрате \ (1 – R в квадрате xi(x)) – (n-m-1)

Для определения ошибки собственного члена не подходит.

R в квадрате xi (x) = r в квадрате

 

Общий критерий Фишера

Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью F-критерия. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F-отношения, т.е. критерий F:

F= Dфакт/Dост = (R²/1-R²) * (n-m-1/m),

где Dфакт – факторная сумма квадратов на одну степень свободы

R² - индекс (коэффициент) множественной детерминации

n – число наблюдений

m – число параметров при переменных x (в линейной регрессии совпадает с числом включенных в модель факторов)

Dост – остаточная сумма квадратов на одну степень свободы.

Величина m характеризует число степеней свободы для факторной суммы квадратов, а (n-m-1) – число степеней свободы для остаточной суммы квадратов.

Применение критерия Фишера предполагает:

1) расчет фактического значения критерия Fфакт

2) по таблице – табличного значения Fтабл

3) сравнение Fфакт и Fтабл, если факт>табл, то оцениваемое уравнение регрессии значимо с вероятностью P= 1-a (альфа), где а- вероятность ошибки.

Общий f-критерий:

, где SSфакт – факторная сумма квадратов =

SSост – остаточная сумма квадратов = , n- кол-во наблюдений, m – кол-во параметров уравнения регрессии без свободного члена

Табличное значение F-критерия – это максимальная величина отношения дисперсий.

Формулу фактического значения часто используют в измененном виде:

Таблица дисперсионного анализа

Оценка значимости уравнения регрессии обычно дается в виде таблицы дисперсионного анализа.

Источники вариации	Число степеней свободы df	Сумма квадратов отклонений	Дисперсия на одну степень свободы (MS=SS/df)	Fфакт	Fтабл, при а=0,05
Регрессия	m	SSфакт = ∑(y^-y¯)²	SSфакт/m	MSфакт/ MSост	Fтабл
Случайные колебания	n-m-1	SSост = ∑(y-y^)²	SSост/ n-m-1	---	---
Общая вариация	n-1	SSобщ = ∑(y-y¯)²	---	---	---

 

 

19.Показатели частной корреляции и детерминации

Для оценки изолирован влияния кажд фактора на рез-т при устранении воздействия прочих факторов модели исп-ся частные показатели корреляции. Показатели частн корреляц представляют собой отношение сокращения остаточной дисперсии за счет дополнит включения в анализ нов фактора к остаточн дисперсии, имевшей место до введения его в модель. 1)индекс частной корреляции для фактора х_1. η _{yx1*x2x3…xn}=корень из (G²_{yx2x3..xm(ост)} – G²_{yx1x2x3..xm(ост)})/G²_{yx2x3..xm(ост)} Под корнем в числителе- сокращение остаточн дисперсии за счет включения в модель фактора x1 после остальных факторов. 2)частный коэф корреляции r_yx1*x2x3..xm=корень из (1-(1– R²_yx1*x2x3..xm)/(1- R²_yx2x3..xm)) Рекурентные формулы расчета частн коэф корреляции 1го порядка: Порядок частн показателя корреляции соотв-ет числу факторных признаков, влияние котор устраняется. Для 2х факторн модели част коэф корреляции:

r_yx1*x2= (r_yx1 - r_yx2* r_x1x2)/корень из((1- r_yx2²)* (1- r_x1x2²)) и

r_yx2*x1= (r_yx2 - r_yx1* r_x1x2)/корень из((1- r_yx1²)* (1- r_x1x2²))

Измеряется от -1 до 1. Исп-ся для оценки целесообразности добавления нов фактора в ур-ние после других факторов. Если частн коэф корреляции стремится к 0, то добавление нов.фактора не целесообразно.

 

20. Частный F-критерий

Для оценки статистич целесообразности добавления нов факторов в регрессион модель исп-ся частн критерий Фишера, т.к на рез-ты регрессион анализа влияет не только состав факторов, но и последовательность включения фактора в модель. Это обьясняется наличием связи между факторами.

F_xj =((R² по yx1x2...xm – R² по yx1x2…xj-1,хj+1…xm)/(1- R² по yx1x2...xm))*((n-m-1)/1)

F_табл (альфа,1, n-m-1) F_xj больше F_табл – фактор x_j целесообразно лючать в модель после др.факторов.

Если рассматривается уравнение y=a+b1x1+b2+b3x3+e, то определяютсяпоследовательно F-критерий для уравнения с одним фактором х1, далее F-критерий для дополнительного включения в модель фактора х2, т. е. дляперехода от однофакторного уравнения регрессии к двухфакторному, и,наконец, F-критерий для дополнительного включения в модель фактора х3, т.е. дается оценка значимости фактора х3 после включения в модель факторов x1их2. В этом случае F-критерий для дополнительного включения фактора х2после х1 является последовательным в отличие от F-критерия длядополнительного включения в модель фактора х3, который является частным F-критерием, ибо оценивает значимость фактора в предположении, что он включенв модель последним. С t-критерием Стьюдента связан именно частный F-критерий. Последовательный F-критерий может интересовать исследователя настадии формирования модели. Для уравнения y=a+b1x1+b2+b3x3+e оценказначимости коэффициентов регрессии Ь1,Ь2,,b3 предполагает расчет трехмежфакторных коэффициентов детерминации.

 

Тест Парка

Тест Парка – нахождение параметров для регрессии следующего вида:

lnE^2=a+bln*xi+б, где

xi - фактор, который предположительно оказывает влияние на дисперсионный остаток

б - случайный остаток (но который остался от др. случ. остатка)

 

Оцен-ся значимость коэффициента b (знач, если t факт>t табл),

если значимый – остатки гетероскедастичны,

если незначим – гомоскед.

 

Тест Глейзера

|E| = а+bxi^k + б

а,b – неизвестные параметры, зависят от ур. регрессии

k – задается произвольно, обычно k может быть равно: -2;-1;-0,5;0,5;1;2.

Дается оценка значимости b, если он значим – гетероскедостичность в остатке (т.е. отсутствие зависимости x от y)

Если изменится форма регрессии, то параметры меняются. t>t табл -> параметры значимы -> гетероскедастичность по определенному фактору (xi).

Если гетероскедостичность хотя бы по одному тесту -> остатки гетероскедостичны в общем и тест Глейзера можно не продолжать

 

Тест Уайта.

используется для анализа гетероскедастичности случайных остатков (E).

Т.е. изменения дисперсии случайных остатков от наблюдения к наблюдению.

Для выбора хорошей модели уравнения регрессии необходимо, чтобы Е были гомоскедастичны, т.е. их дисперсия была постоянна, и не зависела от дисперсии фактора х.

В тесте Уайта моделируется уравнение рессии,сост. из элементов, включающих все факторы, входящие в уравнение регрессии+Эти же факторы в квадрате+необязательная часть,- попарные произведения факторов.

Для случая модели с двумя факторами (x₁ и x₂), ур-я будут иметь вид:

E²=a+b₁₁x₁+b₂₁x₂+b₁₂x₁²+b₂₂x₂²+c₁₂x₁x₂+δ

В рамках теста нужно оценить знач-ть всего ур. в целом, с помощью F-критерия Фишера. Если Fфакт>Fтабл =>Ур. значимо => все ф-ры оказывают влияние на величину Е и => остатки гетероскед-ны. И наоборот.

Из этого Ур-я иногда следует назвать факторы, вызыв-е гетероскед-ть остатков. Это ф-ры, имеющие значимые параметры при них. Находятся ф-ры с помощью t-критерия Стьюдента. Tсли Tфакт>Tтабл => ф-р значим и влияет на остатки, вызывая их гетероскедостичность, если же Tфакт<Tтабл, =>ф-р незначим и не влияет на остатки. Т.е. если Tтабл=2,45,а Tфакт по (x₂)= - 4, можно сделать вывод, что x₂ значим и влияет на гетероскедастичность остатков.(Т.К. значение t-критерия берём по модулю!)

 

 

Тест Гольдфельда-Квандта.

С помощью этого теста исследуются случайные остатки (Е) на предмет гомоскедастичности.

Этапы теста:

1. совок-ть наблюдений упорядочивают по фактору, кот. предположительно влияет на Е.
2. Всю эту совок-ть делят на три группы (n1,n2,n3). При этом, n1 и n3 должны содержать равное кол-во эл-тов(n1=n3). n2 мож.быть =n1 и n3 (Желательно!), или же быть меньше n1 и n3.
3. По 1 и 3 совок-ти строят ур-я регрессии используя Метод Наименьш.Квадратов. Причём они должны иметь ту же структуру, что и исходн. ур-е регр. Т.е. если исходн. ур-е имеет 2 фак-ра (x₁,x₂), то и новые ур-я должны иметь столько же фак-ров.
4. Для кажд.из 2-х ур-й рассчитывают остаточные дисперсии(соответственно SS¹_ост и SS³_ост)
5. Далее находят фактич.знач-е F-критерия, для этого бОлшую остат.дисперсию делят на меньшую. (нпр. SS¹_ост /SS³_ост)
6. Далее находят Fтабл при df₁=df₂=n₁-m-1. Если Fфакт>=Fтабл, то остатки Е гетероскед-ны по тому фактору, по кот.мы проводили упорядоч-ние в 1п.

Например: Отсортируем совок-ть по фактору x2(он предположит-но влияет на Е)

Y x₁ x₂

121 56 28

80 114 36

56 124 42

75 98 46

88 102 50

45 17 54

110 116 54

63 28 56

113 50 63

160 115 88

203 118 105

237 154 106

Разделим совок-ть на 3 гр:n1=n3=n3=4

Построим Ур-я для n1 и n3 вида: y=a +b₁x₁+b₂x₂ +E

y = 193 – 0,64x1 – 1,25x2 + E

y = -17,8 + 0,49x1 + 1,57x2 + E

SSост(1): = 57,1

SSост(3)= 503,3

Fфакт=503,3/57,1= 8,8

df1 = df2 = 4 -2-1 = 1, Fтабл=161,4 => Fфакт<Fтабл, значит х₂ не значим, не влияет на остатки => E – гомоскед-ны

 

Вопрос 30 Применение МНК к одной из парных нелинейных функций регрессии (параболе, гиперболе, степенной, показательной)

Не весь вопрос

После того, как функции были приведены к линейной форме, с ними можно работать как с обычными линейными функциями.

 

К линеаризованным функциям применяется МНК (для нахождения параметров уравнения регрессии)

 

Применение MНК для оценки параметров параболы второй степени приводит к след системе нормальных уравнений:

∑y= n*a + b*∑x + c* ∑x^2

∑y*x= a*∑x + b*∑x^2 + c*∑x^3

∑y*x^2 = a*∑x^2 + b*∑x^3 + c* ∑x^4

 

Решить ее относительно параметров a, b и с можно методом определителей:

a= ∆a/∆; b=∆b/∆; c=∆c/∆

 

 

Вопрос 31 Коэффициент эластичности для нелинейных функций.

Э = f ‘ (x)* x / f (x) – общая формула. Потом коэф эласт рассчит для каждой конкретн функции через произв:

Парабола (парабола второго порядка):

Y=a + bx +cx^2 + E

Y ‘ = b+2c, следовательно

Э = ((b + 2*c*x) *x)/ (a+b*x+c*x^2)

Как и в лин функции вместо x часто подставляют x средн. Для общей хар-ки эластичности, но это не ведет к упрощению. (Э ср. = b*x cр./ y ср.)

Гипербола: Э = -b/ (a*x + b)

Показательная: Э = x * ln b

Степенная:

F ‘ (x) = a*b*x^(b-1) соответственно Э = b

№ 35 – Прогнозирование по нелинейным по параметрам функциям регрессии (степенной, показательной)

Особенности прогнозирования по нелинейным функциям заключается в том, что сначала точечный и интервальный прогноз оценивается по линеаризованной форме, а затем при необходимости значение прогноза пересчитывается для исходной формулы. Необходимость возникает, когда функции были нелинейными по параметрам и следовательно зависимая переменная у была преобразована (пролонгирована).

y=a+b/x +E

y=a+bx+E

x(среднее)=1/x

yпр+(-)t(табличное)*m(упр)

y=ax^bE

lny=lna+blnx+lnE

Y=A+BX+E

Y(выровненный), пролонгированный=5 y(выровненный), пролонгир=е^yпр=е^5

Y пролонгир.min=3 y пролонгир.min= е^3

Yпролонгир.max=7 y пролонгир.min=е^7