Статистична гіпотеза – це певне припущення щодо властивостей генеральної сукупності, яке можна перевірити за даними вибірки.
Розрізняють нульову та альтернативну гіпотези.
Нульова – це гіпотеза, яку потрібно перевірити. Вона формулюється як відсутність розбіжності (нульова розбіжність) між невідомим параметром генеральної сукупності G та заданою величиною А.
Зміст нульової гіпотези записується після двокрапки: H0 : G = A.
Альтернативна – це гіпотеза, протилежна нульовій. Вона може бути задана так:
|
Hа: G > А
На: G < А
|
На:G ≠ A
Якщо дані вибірки узгоджуються з нульовою гіпотезою, вона приймається; якщо ні –відхиляється. У ході перевірки гіпотез існує два види ризику:
- ризик І – відхилення правильної нульової гіпотези;
- ризик II – прийняття помилкової нульової гіпотези.
Імовірність ризику І називається рівнем істотності (межею малоімовірності) і позначається а. Рівень істотності – це мінімальна імовірність, починаючи з якої подія визнається практично неможливою.
Межа малоімовірності (рівень істотності) а задається окремо в кожному випадку. Найчастіше використовують значення а = 0,1; 0,05; 0,025; 0,01. Рівень істотності а = 0,05 означає, що лише в 5 випадках зі 100 існує ризик відхилити правильну нульову гіпотезу.
Процедура перевірки гіпотез ґрунтується на понятті статистичного критерію.
Статистичний критерій – це оціночний показник, обчислений за даними вибірки, на основі якого нульова гіпотеза приймається або відхиляється.
Математичною основою будь-якого параметричного критерію є статистична характеристика Z, закон розподілу якої відомий. Кожне значення характеристики Z має певну імовірність.
Для названих вище рівнів істотності існують таблиці критичних значень статистичних критеріїв. Наприклад, критичні значення t-критерію Стьюдента для імовірності 0,95:
| Число ступенів вільності | t для інтервалу | Число ступенів вільності | t для інтервалу | ||
| одностороннього | двостороннього | одностороннього | двостороннього | ||
| 6,3138 | 12,7060 | 1,7341 | 2,1009 | ||
| 2,9200 | 4,3027 | 1,7291 | 2,0930 | ||
| 2,3534 | 3,1825 | 1,7247 | 2,0860 | ||
| 2,1318 | 2,7764 | 1,7207 | 2,0796 | ||
| 2,0100 | 2,5706 | 1,7171 | 2,0739 | ||
| 1,9432 | 2,4469 | 1,7139 | 2,0687 | ||
| 1,8946 | 2,3646 | 1,7109 | 2,0639 | ||
| 1,8595 | 2,3060 | 1,7081 | 2,0595 | ||
| 1,8331 | 2,2622 | 1,7056 | 2,0555 | ||
| 1,8125 | 2,2281 | 1,7033 | 2,0518 | ||
| 1,7959 | 2,2010 | 1,7011 | 2,0484 | ||
| 1,7823 | 2,1788 | 1,6991 | 2,0452 | ||
| 1,7709 | 2,1604 | 1,6973 | 2,0423 | ||
| 1,7613 | 2,1448 | 1,6839 | 2,0211 | ||
| 1,7530 | 2,1315 | 1,6707 | 2,0003 | ||
| 1,7459 | 2,1199 | 1,6577 | 1,9799 | ||
| 1,7396 | 2,1098 |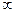 
| 1,6449 | 1,9600 |
Критичне значення критерію – 
– це його максимально можливе значення, яке може виникнути випадково.
Критичне значення поділяє множину вибіркових значень Z на дві частини:
- область допустимих значень;
- критичну область.
Якщо вибіркове значення Z потрапляє в критичну область, нульова гіпотеза відхиляється, якщо в область допустимих значень – приймається.
Залежно від того, як сформульована альтернативна гіпотеза, критична область може бути односторонньою (ліво- або правосторонньою) або двосторонньою. За двосторонньої перевірки гіпотези використовують критичне значення для а /2, наприклад, при а = 0,05 – Z0,975.
Алгоритм статистичної перевірки гіпотез
1. Сформулювати нульову та альтернативну гіпотези.
2. Вибрати статистичну характеристику Z, за значенням якої буде перевірятись правильність нульової гіпотези.
3. Визначити рівень істотності а і відповідне йому критичне значення , з'ясувавши, якою буде критична область – одно - чи двосторонньою.
4. За результатами вибірки обчислити вибіркове значення статистичної характеристики Z і порівняти його з критичним:
якщо Z >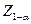 
, гіпотеза Но відхиляється;
якщо Z < 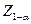, гіпотеза Но не відхиляється.
У ході перевірки гіпотези про істотність розбіжностей середніх двох сукупностей нульова гіпотеза формулюється як відсутність розбіжності, тобто Но: 
.
Тоді На: 
.
Статистичною характеристикою цієї нульової гіпотези є нормоване відхилення середніх:
,
де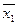 
, 
– середні значення ознаки відповідно в першій та другій сукупності;
n1, n2 – обсяги сукупностей;
S2 – оцінка дисперсії, яка обчислюється за формулою:
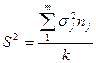
де 
– дисперсія досліджуваної ознаки в j -тій сукупності.
k – число ступенів свободи (вільності) варіації.
k = n1 + n2 – 2.
Число ступенів вільності варіації – кількість варіант, які можуть мати довільні значення, за умови, що при цьому не зміниться середнє значення ознаки в сукупності.
1. З метою перевірки ефективності нового пристрою для вдосконалення технології обробки деталей робітників бригади поділили на дві групи: на верстатах з новим пристроєм працювало 4 робітники, за традиційною технологією обробки деталей – 6.
Результати експерименту такі: у першій групі середній виробіток за години становить 84 деталі при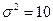 
, у другій – 77 деталей при 
.
Сформулюйте нульову та альтернативну гіпотези. За допомогою t-критерію Стьюдента з рівнем істотності 0,05 зробіть висновок, чи дійсно нова технологія впливає на продуктивність праці.
Нульова гіпотеза: H0 :, тобто
Альтернативна гіпотеза (вказати, якою буде перевірка нульової гіпотези – односторонньою чи двосторонньою):
Hа:, тобто
Обчислити оцінку дисперсії виробітку:
Обчислити нормоване відхилення середніх значень виробітку:
Визначити число ступенів свободи варіації виробітку:
За таблицею критичних значень t-критерію Стьюдента знайти критичне значення для встановленого числа ступенів свободи варіації та рівня істотності 0,05:
Порівняти фактичне значення t-критерію з його критичним значенням:
Зробити висновок щодо прийняття чи відхилення нульової гіпотези та щодо впливу нової технології на продуктивність праці.
Висновок:
2. Відомі такі дані про розподіл робітників другого та шостого розрядів за розміром заробітної плати:
| Заробітна плата, грн | Кількість робітників, чол. | |
| другого розряду | шостого розряду | |
| До 1200 | ||
| 1200 – 1400 | ||
| 1400 – 1600 | ||
| 1600 – 1800 | ||
| 1800 і більше |
Сформулюйте нульову та альтернативну гіпотези стосовно відмінностей у розмірі середньої заробітної плати в обох сукупностях.
За допомогою t-критерію Стьюдента з імовірністю 0,95 перевірте висунуту нульову гіпотезу.
Задача відрізняється від попередньої тим, що за даними умови слід самостійно визначити середню заробітну плату та дисперсію заробітної плати окремо для робітників другого та шостого розрядів. Порядок розрахунків аналогічний розрахункам в задачі № 1 теми „Вибіркове спостереження”.
Всі необхідні обчислення виконати в таблицях:
Таблиця 1
Розрахунок середнього значення та дисперсії заробітної плати робітників другого розряду
| Разом |
=
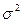Таблиця 2
Розрахунок середнього значення та дисперсії заробітної плати робітників шостого розряду
| Разом |
=
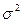Далі – хід розв’язку аналогічний розв’язку попередньої задачі.
Сформулювати нульову гіпотезу: H0 :, тобто
Альтернативна гіпотеза (вказати, якою буде перевірка нульової гіпотези – односторонньою чи двосторонньою):
Hа:, тобто
Обчислити оцінку дисперсії заробітної плати:
Обчислити нормоване відхилення середніх значень заробітної плати:
Визначити число ступенів свободи варіації заробітної плати:
За таблицею критичних значень t-критерію Стьюдента знайти критичне значення для встановленого числа ступенів свободи варіації та рівня істотності 0,05:
Порівняти фактичне значення t-критерію з його критичним значенням:
Зробити висновок щодо прийняття чи відхилення нульової гіпотези та щодо впливу рівня кваліфікації робітників на розмір їх заробітної плати.
Висновок:
