Обозначение графических материалов
Целевое назначение
1 Изучение ГОСТов: форматы чертежей, шрифты чертежные, линии, обозначение графических материалов и нанесение размеров.
2 Освоение приемов работы чертежными инструментами, а также выполнение надписей стандартным чертежным шрифтом.
Содержание Работа является общей для всех студентов. Пример выполнения дан на рисунке А.1.
Оформление Работу выполнить на формате А3.
Порядок выполнения
1 Изучить ГОСТ 2.301-68, 2.303-68, 2.304-81, 2.306-68, 2.307-68.
2 Изучить правила обращения с чертежными инструментами.
3 Подготовить рабочее место: бумагу, чертежные принадлежности, пособия. Все лишнее убрать. Прочитать рекомендации по выполнению работы в данном пособии.
4 Вычертить рамку и штамп.
5 Поле чертежа разделить на две части. Наметить места расположения заданий.
6 В левой части листа выполнить карандашом шрифт, предварительно нанеся сетку и придерживаясь начертания букв и цифр, указанных в ГОСТ 2.304-81, и начертания линий чертежа согласно приведенному примеру (рисунок А.1).
7 В правой стороне листа вычертить обозначения графических материалов по типу, указанному в ГОСТ 2.306-68, и примеры по нанесению размеров на чертежах согласно ГОСТ 2.307-68.
8 Выполнить надписи на чертеже и заполнить основную надпись, предварительно построив сетку. Все линии независимо от их назначения – надписи, шрифт и цифры - выполнять карандашом тонкими линиями толщиной s≈0,15 мм.
9 Проверить правильность всех построений и надписей.
10.Выполнить обводку линий и надписей карандашом, принимая толщину сплошных линий s=0,8 – 1,0 мм, толщину остальных линий согласно ГОСТ 2.303-68.
10 Проверить чертеж и надписи, очистить резинкой поле чертежа от лишних линий и загрязнений.
Сопряжения, уклон, конусность
Целевое назначение
1 Изучение построений уклона и конусности.
2 Изучение построений сопряжений.
Содержание
1 Построить чертеж валика (рисунок 1) и профиль двутавровой балки (рисунок 2) или швеллера (рисунок 3).
2 Построить сопряжения.
Пример выполнения работы дан на рисунке А.2.
Профиль двутавровой балки или швеллера, а также чертеж валика выполняются по индивидуальным заданиям (таблицы 1-3). Задания на сопряжения являются общими для всех студентов.
Номер варианта выдается преподавателем.

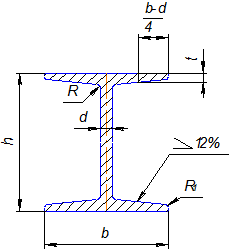
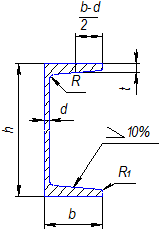
Рисунок 1 Рисунок 2 Рисунок 3
Таблица 1-Валик
| Номер варианта | L | h | D | b | a | Конус-ность | Фаска | |
| мм | Высота,мм | Угол, град | ||||||
| 1,2,3 | 1:5 | |||||||
| 4,5,6 | 1:8 | |||||||
| 7,8,9 | 1:5 | |||||||
| 10,11,12 | 10% | |||||||
| 13,14,15 | 15% | |||||||
| 16,17,18 | 10% | |||||||
| 19,20,21 | 1:5 | |||||||
| 22,23,24 | 1:5 | |||||||
| 25,26,27 | 1:8 |
Таблица 2 – Двутавровая балка (по ГОСТ 8239)
| Номер варианта | Номер профиля | Размеры, мм | |||||
| h | b | d | t | R | R1 | ||
| 1,2,3 | 4,5 | 7,2 | 2,5 | ||||
| 4,5,6 | 4,8 | 7,3 | 7,5 | ||||
| 7,8,9 | 4,9 | 7,5 | |||||
| 10,11,12 | 5,0 | 7,8 | 8,5 | 3,5 | |||
| 13,14,15 | 5,1 | 8,1 | 3,5 |
Таблица 3 – Швеллер (по ГОСТ 8240)
| Номер варианта | Номер профиля | Размеры, мм | |||||
| h | b | d | t | R | R1 | ||
| 16,17,18 | 4,5 | 7,6 | |||||
| 19,20,21 | 4,8 | 7,8 | 7,5 | ||||
| 22,23,24 | 14а | 4,9 | 8,7 | ||||
| 25,26,27 | 16а | 8,5 | 8,5 | 3,5 |
Оформление
Графическую работу выполняют на листе чертежной бумаги, формата А3 карандашом.
Порядок выполнения
1 Ознакомиться с построением конусности, уклона и сопряжения.
2 Подготовить рабочееместо.
3 На листебумаги формат А3 оформить рамку и основную надпись.
4 Внимательно изучитьгеометрические фигуры, подлежащие вычерчиванию и наметить на листе места расположения валика, профилябалки и сопряжений.
5 Выполнить все необходимые построения по каждому заданию. Вычертив валик, следует переходить к следующему (профиль балки или швеллера), затем к примеру 1 на сопряжения и т. д. (рисунок А.2).
6 Оформить надписи. Наименование фигур писать размером шрифта 5 или 7. Все линии чертежа и надписи выполнить карандашом тонкими линиями толщиной 0,15—0,20 мм.
7 Проверить правильность выполненных заданий и приступить к обводке карандашом.
8 Очистить поле чертежа от загрязнений.
При выполнении работы пользоваться вышеуказанной литературой и ГОСТ 2.303—68, 2.304—68, 2.306—68 2.307—68.
Методические указания
1 Уклон прямой характеризует ее наклон к другой прямой, обычно горизонтальной и реже вертикальной. Уклон выражается отношением противолежащего катета ЕС к прилежащему катету АС. Он представляет собой (рисунок 4)
 .
.
Конусностью называется отношение диаметра окружности основания прямого конуса к его высоте (рисунок 5), а для усеченного конуса — отношение разности диаметров оснований к его высоте, т. е.
 .
.
При одном и том же угле α конусность в два раза больше уклона. Уклон и конусность могут быть выражены простой и десятичной дробью, а также в процентах.


Рисунок 4 Рисунок 5
Согласно ГОСТ 2.307—68 перед размерным числом, определяющим уклон, наносят знак,острый угол которого должен быть направлен в сторону уклона (рисунок 4); перед размерным числом, характеризующим конусность, наносят знак, вершина которого должна быть направлена в сторону вершины конуса (рисунок 5).
2 При выполнении чертежа валика буквенные значения, данные на рисунке 1 надо заменить цифровыми. Квадрат при отсутствии проекции, определяющей его конфигурацию, следует обозначить знаком, который проставляется перед размерным числом стороны квадрата, например 12. Диагональные линии проводятся толщиной s/3.
По ГОСТ 2.307—68 размеры фасок под углом 45° наносят, как показано на рисунке 6,а. Размеры фасок под другими углами указывают по общим правилам — линейным и угловым размерами (рисунок 6,б) или двумя линейными размерами (рисунок 6,в).

а б в
Рисунок 6 –Обозначение фасок на чертеже
3 При выполнении профиля швеллера или двутавровой балки все размеры берут из таблицы и на чертеже вместо буквенных выражений ставят цифровые. Для построения заданного уклона необходимо рядом с профилем построить прямоугольный треугольник, тангенс угла которого равен уклону, затем через точку, положение которой на профиле определяется размерами
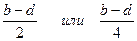 ,
,
провести прямую (рисунок А.2), параллельную гипотенузе построенного прямоугольного треугольника. Штриховку профиля выполняют в соответствии с ГОСТ 2.306—68. При обводке карандашом построение уклона на чертеже надо показать тонкими сплошными линиями.
4 Сопряжением называется плавный переход от прямой линии к дуге окружности или от одной дуги окружности к другой. Точкой сопряжения называется общая точка двух сопрягаемых линий. Сопряжения имеют большое применение в очертаниях технических форм. Построение сопряжений основано на двух положениях из геометрии:
а) для сопряжения прямой линии и дуги необходимо, чтобы центр окружности, которой принадлежит дуга, лежал на перпендикуляре к прямой, восстановленном из точки сопряжения (рисунок 7,а);
б) для сопряжения двух дуг необходимо, чтобы центры окружностей, которым принадлежат дуги, лежали на прямой, проходящей через точку сопряжения и перпендикулярной к общей касательной этих дуг (рисунок 7,б).

а б в
Рисунок 7 – Построение сопряжений
Для выполнения сопряжений между двумя прямыми линиями от прямой линии к окружности и от одной дуги окружности к другой при помощи некоторой дуги имеются три элемента построения: радиус дуги перехода, центр дуги перехода, точка сопряжения. Задается один из этих элементов (например, радиус), элементы должны быть получены построением. В примере 1 (рисунок А.2) дан радиус 20 мм, найдены точки сопряжения и центр дуги. Для этого проведены линии, параллельные заданным, на расстоянии, равном 20 мм, точка пересечения которых дает искомый центр дуги. Опуская перпендикуляры на заданные прямые, находим точки сопряжения. В этом же примере дана точка сопряжения А, определены радиус и центр дуги сопряжения. Искомый центр дуги лежит на перпендикуляре, восстановленном к заданной прямой в точке А, а также на биссектрисе угла между заданными прямыми.
В примере 2 (рисунок А.2) дан радиус 10 мм, найдены центр дуги, точки сопряжения. Для этого проведена прямая, параллельная заданной, на расстоянии 10 мм и дуга радиуса, равного
 .
.
Искомый центр дуги R 10 лежит на пересечении прямой с проведенной дугой. Точки сопряжения лежат на пересечении перпендикуляра, опущенного из центра на прямую, и на линии, соединяющей центры заданной окружности диаметром 40 мм и искомой дуги.
Дана точка сопряжения В на окружности; определены центр дуги, радиус и вторая точка сопряжения. Искомый центр дуги лежит на линии, проходящей через центр окружности и точку В, а также на биссектрисе угла, образованного заданной прямой и касательной, проведенной через точку В.
Дана точка сопряжения С на прямой; определены центр дуги, радиус и вторая точка сопряжения. Для нахождения центра и дуги через заданную точку С проведен перпендикуляр к прямой, отложено расстояние, равное радиусу окружности диаметром 40 мм; полученная точка соединена с центром окружности и из середины отрезка восставлен перпендикуляр, пересечение которого с перпендикуляром, восстановленным из точки С, дает искомый центр дуги.
В примере 3 (рисунок А.2) дан радиус 45 мм сопряжения двух дуг, определены центр дуги и точки сопряжения. Искомый центр дуги лежит на пересечении дуг радиусов, равных заданному R45, плюс радиусы сопряженных окружностей. Дана точка D, определены центр дуги, радиус и вторая точка сопряжения. Нахождение центра дуги подобно нахождению центра дуги в примере 2 при заданной точке сопряжения С.
Все построения на чертеже должны быть сохранены.
Вопросы для самопроверки
1 Что называется уклоном, конусностью?
2 Как обозначаются уклон и конусность на чертеже?
3 Как обозначают конические фаски на чертежах?
4 Нарисуйте линию обрыва круглого металлического прутка.
5 На каких двух положениях из геометрии основано построение сопряжений?
6 Перечислите три элемента сопряжений.






