9) Момент инерции и его вычисление. Теорема Штейнера.
Момент инерции — скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения СИ: кг·м².
Обозначение: I или J.
Момент инерции осевые и центробежные. Осевым Момент инерции тела относительно оси z называется величина, определяемая равенством:

Центробежным Момент инерции относительно системы прямоугольных осей х, у, z, проведённых в точке О, называют величины, определяемые равенствами:

теорема Штейнера: момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jс относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями:

где
Jс — известный момент инерции относительно оси, проходящей через центр масс тела,
J — искомый момент инерции относительно параллельной оси,
m — масса тела,
d — расстояние между указанными осями.
10) Момент силы — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
Единицы измеренияСИ Ньютон-метр. 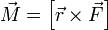 В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр. Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метров от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров до оси вращения. Более точно, момент силы частицы определяется как векторное произведение:
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр. Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метров от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров до оси вращения. Более точно, момент силы частицы определяется как векторное произведение:
где — Fсила, действующая на частицу, а r — радиус-вектор частицы.
Основной закон динамики вращательного движения в традиционной механике формулируется так, что первая производная по времени t от момента импульса L механической системы относительно любой неподвижной точки О равна главному моменту М внешних относительно той же точки О всех внешних сил приложенных к системе:
dL/ dt = M внеш. Закон динамики вращательного движения аналогичен второму закону неинерциальной импульсной механики d P / dt = F, в котором изменение момента импульса движения dР для тела массой m и ускорением - а по времени dt, заменен на изменение момента импульса вращения dL/dt.
11) Моме́нт и́мпульса характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.
Зако́н сохране́ния моме́нта и́мпульса (закон сохранения углового момента) — векторная сумма всех моментов импульса относительно любой оси для замкнутой системы остается постоянной в случае равновесия системы. В соответствии с этим, момент импульса замкнутой системы относительно любой неподвижной точки не изменяется со временем.
Закон сохранения момента импульса есть проявление изотропности пространства.
12 ) Кинетическая энергия тела, движущегося произвольным образом, равна сумме кинетических энергий всех n материальных точек па которые это тело можно разбить: 
Если тело вращается вокруг неподвижной оси с угловой скоростью  , то линейная скорость i-ой точки равна
, то линейная скорость i-ой точки равна 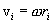
, где  - расстояние от этой точки до оси вращения. Следовательно.
- расстояние от этой точки до оси вращения. Следовательно. 
где J - момент инерции тела относительно оси вращения.
Рассчитаем работу силы, вызывающей вращательное движение тела вокруг некоторой оси и приложенной к произвольной точке этого тела. Согласно определению работы имеем:
dA = F·ds = Ft·ds.
Поскольку ds = r·da, то получим следующее выражение для работы:
dA = Ft·r·da = M·da.






