Методические указания по выполнению работы

Лабораторная работа 1

АНАЛИЗ СТАТИСТИЧЕСКОГО РЯДА

Цель работы: Провести статистическую обработку данных, содержащихся в информационном сообщении в виде одномерного числового массива.

Общие положения

Информационное сообщение представляет собой одномерный числовой массив вида

(х₁, х₂, …, х_n), (1)

где n – число данных (размерность массива).

Массив (1) моделируется следующим образом. Число n устанавливается равным числу букв, содержащихся в фамилии и имени студента. Определяются порядковые номера букв, составляющих фамилию и имя и заносятся в табл. 1. Например, студента зовут Белов Денис. В данном случае размерность массива n = 10, а его элементы примут следующие значения: х₁ = 2 (так как первой букве «Б» фамилии соответствует порядковый номер 2, х₂ = 6 (второй букве «Е» соответствует 6) и т.д. до х₁₀.

Расчеты требуется выполнить вручную и с использованием одного из пакетов прикладных программ.

Методические указания по выполнению работы

Процесс принятия решений в области управления качеством должен базироваться в первую очередь на фактах, а не на интуиции. Следовательно, нужно организовать процесс поиска фактов, т.е. сбора и обработки статистических данных.

Пусть в качестве исходной информации выступают статистические данные, представляющие собой последовательность значений некоторой величины, полученных в результате измерений. Данную величину, значения которой невозможно предсказать до момента их появления, назовем случайной. Генеральная совокупность – совокупность всех значений, которые может принимать случайная величина. Выборка – часть данных, полученных из генеральной совокупности.

В предположении, что массив (1) представляет собой выборку объемом n для некоторой случайной величины Х, производится оценка всех числовых характеристик распределения этой величины.

Наиболее важными числовыми характеристиками случайной величины (СВ) являются следующие:

– характеристики центра распределения;

– характеристики рассеивания случайной величины около ее математического ожидания;

– характеристика асимметрии распределения и его эксцесса.

В лабораторной работе необходимо рассчитать следующие числовые характеристики центра распределения: среднее значение, медиану и моду.

Среднее значение или оценка математического ожидания вычисляется по формуле среднего арифметического, т.е.

Заметим, что оценка математического ожидания дискретной СВ может вычисляться как сумма произведений всех возможных значений СВ на вероятности этих значений, т.е.

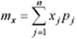
где p_j – вероятность j-го значения СВ.

Значение m_x характеризует как бы «центр тяжести» распределения СВ. Наряду с математическим ожиданием центр распределения определяют медиана и мода.

Медианой СВ называется такое значение Me_x, для которого с одинаковой вероятностью значения Х может оказаться меньше Me_x и больше Me_x. (значение, расположенное в середине ряда). Для расчета медианы Me_x массив (1) записывается в виде ранжированного ряда:

(х₁ ^p, х₂ ^p, …, х_n ^p), (3)

 

где значения х_i расставлены в порядке возрастания (или убывания). Пример получения ранжированного ряда представлен в табл. 1.

Таблица 1

 

В случае, если n – четное, медиана равна

при нечетном n

В нашем примере

При малом n медиана наиболее устойчиво характеризует центр распределения СВ Х.

Модой Mо_x называется наиболее вероятное значение СВ. В качестве оценки моды в ранжированном ряду (3) берется значение с x_j^р, которое повторяется большее число раз (имеет большую частоту).

Для данных, приведенных в табл. 1

Распределение СВ может характеризоваться несколькими модами, такое распределение называют полимодальным. Применительно к данным табл. 1 можно указать второе значение моды

Если массив (1) не содержит повторяющихся значений, то значение моды оценивается после построения гистограммы.

Необходимо отметить, что оценки ˆ m_x, ˆ Me_x., ˆ Mо_x могут как совпадать, так и существенно различаться.

В лабораторной работе необходимо рассчитать следующие числовые параметры характеристики рассеивания значений СВ около ее математического ожидания m_x: дисперсию, среднее квадратичное отклонение, размах варьирования, среднее линейное отклонение от математического ожидания, коэффициент вариации и коэффициент осцилляции.

Основной характеристикой рассеивания значений СВ около ее математического ожидания m_x является дисперсия D_x.

Дисперсией СВ Х называется математическое ожидание квадрата центрированной величины. Центрированная случайная величина X^* получается из исходной Х вычитанием ее математического ожидания ˆ m_x, таким образом, X^* имеет нулевое математическое ожидание.

Оценка дисперсии рассчитывается по формуле

Дисперсия имеет размерность квадрата СВ. Непосредственно с дисперсией связана другая характеристика рассеивания – среднее квадратичное отклонение σ_х, оценка его вычисляется по формуле

Эта числовая характеристика имеет размерность СВ Х.

Рассеивание значений Х характеризуется также размахом варьирования R, который равен

Среднее линейное отклонение от m_x рассчитывается по формуле

 

Для оценки рассеивания относительно среднего m_x используют коэффициент вариации ν, (коэффициент вариации по квадратическому отклонению) вычисляемый в процентах

и коэффициент осцилляции (коэффициент вариации по размаху)

Аналогично рассчитывается коэффициент вариации по абсолютному отклонению.

С точки зрения качества продукции, коэффициенты вариации должны быть минимальными.

В качестве числовой характеристики асимметрии распределения СВ применяется коэффициент асимметрии A_S. Его оценка вычисляется по формуле

где ˆµ₃ – оценка третьего центрального момента СВ, равная

Если A_S > 0, то имеет место положительная или правостороння асимметрия, если A_S < 0, то отрицательная или левосторонняя (см. рис. 1). Если распределение симметрично относительно математического ожидания, то A_S = 0.

Островершинность или плосковершинность распределения СВ описывается с помощью числовой характеристики E_к, называемой эксцессом. Значение E_к оценивается по формуле

где ˆµ₄ – оценка четвертого центрального момента, равная

Рис. 1. Виды асимметрии распределения СВ X

 

Рис. 2. Виды распределения СВ Х при различных значениях эксцесса

 

Для нормального распределения ˆ E_к = 0. В случае положительного эксцесса (ˆ E_к > 0) распределение имеет островершинный характер, при ˆ E_к < 0 – плосковершинный (рис. 2). В последнем случае (ˆ E_к < 0) в выводах можно отмечать качественную неоднородность массива (1).

Содержание отчета

1. Название работы.

2. Цель работы.

3. Исходные данные.

4. Формулы и результаты расчета значений характеристик центра распределения (среднее значение, медиана и мода).

5. Формулы и результаты расчета характеристик рассеивания случайной величины около ее математического ожидания (дисперсия, среднее квадратичное отклонение, размах варьирования, среднее линейное отклонение, коэффициент вариации и коэффициент осцилляции).

6. Формулы и результаты расчета характеристик асимметрии и эксцесса распределения СВ.

7. Результаты расчета с использованием пакета прикладных программ с необходимыми пояснениями.

8. Выводы по результатам обработки данных.

Контрольные вопросы

1. Каковы основные характеристики центра распределения СВ?

2. Перечислите характеристики рассеивания СВ около ее математического ожидания.

3. Дайте понятие характеристик асимметрии и эксцесса.

 

 

Приложение 1