Мета роботи. Визначити коефіцієнти активності розчиненої речовини та розчинника.
Методика роботи. Термодинамічну активність розчиненої речовини можна визначити, якщо експериментально виміряти певну властивість розчину і скористатися для розрахунку рівнянням, що пов'язує виміряну властивість з концентрацією, замінивши в цьому рівнянні концентрацію на активність. Обов'язковою умовою при цьому є вимога, щоб згадане рівняння мало точне термодинамічне обгрунтування. Такі вимоги задовольняє рівняння (4) роботи № 2/1. Заради зручності використання його можна переписати в такій формі
(1)
де, згідно з рівнянням (9) роботи № 2/1,
(2)
а kкр - кріоскопічна стала розчинника.
Інтегрування рівняння (1) пов'язано з певними труднощами. Річ у тім, що стандартний стан для розчиненої речовини (на відміну від розчинника) обирають, як правило, на основі закону Генрі, тобто таким чином, щоб активність збігалася з концентрацією в безмежно розведених розчинах. Тому "при інтегруванні в границях від 0 до m по нижній границі виникає 
. Для подолання цієї незручності використовується нова змінна j, яка визначається рівнянням:
(3)
Диференціал j дорівнює:
(4)
Підставивши рівняння (4) в (1), маємо:
(5)
або
(6)
При інтегруванні цього рівняння врахуємо, що в безмежно розведеному розчині 
, бо для такого розчину справедливою є рівність (7) з роботи № 2/1. Тоді
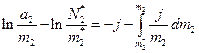(7)
Оскільки
(8)
остаточно маємо:
(9)
Останні рівняння свідчать, що, хоча у вихідному рівнянні (1) стоїть безрозмірна активність а2, безпосередньо із кріоскопічних вимірювань визначається не раціональний коефіцієнт активності 
, а практичний 
. Інтеграл у рівнянні (9) береться графічно, як площа під кривою, побудованою в координатах j/m2 – m2 у границях від 0 до m2
Порядок роботи. Приготувати серію із шести розчинів досліджуваної речовини в інтервалі концентрацій від 0 до 4-5 m. За методикою, описаною у роботі № 2/1, визначити температуру замерзання кожного розчину, а також чистого розчинника. Розрахувати ΔT, j(за рівнянням (3)) та j/m2. Побудувати залежність величини j/m2 від моляльності розчину m2. Виміряти значення площ під кривою в інтервалах від 0 до кожної з досліджуваних концентрацій m2
(10)
Розраховати lnγm та γm для кожного з розчинів. Результати експериментальних вимірювань та розрахунків звести у таблицю за формою:
| № | m2 | ΔT | j | j/m2 | Sm2 | lnγm | γm |
Оскільки в області невеликих концентрацій відношення j/m2 часто буває сталою величиною, значення інтеграла Sm2 за такої умови дорівнює:
(11)
Тоді відповідно до рівняння (9)
(12)
Одержані результати проаналізувати з цієї позиції, зіставивши, зокрема, дані четвертої та шостої колонок таблиці.
За значеннями ΔT,що містяться в другій колонці, можна також розрахувати активність розчинника а1. Для цього можна скористатись наближеним рівнянням (2) з роботи № 2/1 або дещо точнішим, яке можна одержати інтегруванням рівняння (1) з роботи № 2/1 з урахуванням температурної залежності ентальпії плавлення розчинника. Останню можна виразити рівнянням Кірхгофа:
(13)
де ΔHпл - ентальпія переходу 1 моля твердого розчинника в розчин з концентрацією m2 за температури Т; ΔН*ПЛ - ентальпія переходу 1 моля твердого розчинника в рідкий стан за 
за температури Т0; ΔСР - різниця мольних теплоємностей рідкого і твердого розчинника, наближено приймається сталою.
Підставляючи рівняння (13) в (1) з роботи № 2/1 й інтегруючи, одержимо:
(14)
Логарифм у другому доданку можна розкласти в ряд:
(15)
Якщо обмежитись першими двома членами ряду, то рівняння (14) можна переписати:
(16)
Якщо ж прийняти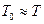 
, то одержимо ще більш наближене рівняння:
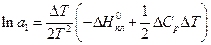(17)
Так, для водних розчинів 
; 
; 
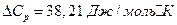. Тоді:
(18)
Активність розчинника а1 з рівнянь (1), (2), (14) та (18) є безрозмірною, тобто такою, що заміняє концентрацію, виражену мольними частками. Тому, розділивши її на мольну частку розчинника, можна одержати значення раціонального коефіцієнта активності 
.
Література: [21, с. 75-86; 24, с. 363-367].
