если задана матрица весов (длин, пропускных способностей) Р:
v 1 v 2 v 3 v 4 v 5 v 6

□ Построим сеть:

а) Найдем величину минимального пути и сам путь сети G. Использу-ем для этого алгоритм Дейкстры.
Этап 1. Нахождение длины кратчайшего пути.
 .
.
Шаг 1. Полагаем 

1-я итерация.
Шаг 2. Составим множество вершин, непосредственно следующих за  с временными метками:
с временными метками:  . Пересчитываем вре-менные метки этих вершин:
. Пересчитываем вре-менные метки этих вершин:  ,
,
 .
.
Шаг 3. Одна из временных меток превращается в постоянную: 
Шаг 4. 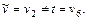 Следовательно, возвращаемся на второй шаг.
Следовательно, возвращаемся на второй шаг.
2-я итерация.
Шаг 2. 

Шаг 3. 
Шаг 4.  Переход на второй шаг.
Переход на второй шаг.
3-я итерация.
Шаг 2. 

Шаг 3. 
Шаг 4.  Переход на второй шаг.
Переход на второй шаг.
4-я итерация.
Шаг 2. 
Шаг 3. 
Шаг 4.  Переход на второй шаг.
Переход на второй шаг.
5-я итерация.
Шаг 2. 
Шаг 3. 
Шаг 4.  Конец первого этапа.
Конец первого этапа.
Следовательно, длина кратчайшего пути равна  .
.
Этап 2. Построение кратчайшего пути.
1-я итерация.
Шаг 5. Составим множество вершин, непосредственно предшеству-ющих  с постоянными метками:
с постоянными метками:  Проверим равенство
Проверим равенство

для этих вершин:
 т.е.
т.е.

 т.е.
т.е.

Включаем дугу  в кратчайший путь,
в кратчайший путь, 
Шаг 6.  Возвращаемся на пятый шаг.
Возвращаемся на пятый шаг.
2-я итерация.
Шаг 5. 


Включаем дугу  в кратчайший путь,
в кратчайший путь,  .
.
Шаг 6.  . Завершение второго этапа.
. Завершение второго этапа.
Следовательно, кратчайший путь построен. Его образует последователь- ность дуг:  .
.
Окончательно, кратчайший путь от вершины 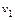 до вершины v 6 пост-роен. Его длина (вес) равна
до вершины v 6 пост-роен. Его длина (вес) равна  . Сам путь образует последова-тельность дуг:
. Сам путь образует последова-тельность дуг:

б) Определим максимальный поток  через сеть G. Для этого используем алгоритм Форда – Фалкерсона.
через сеть G. Для этого используем алгоритм Форда – Фалкерсона.


Выбираем произвольно путь из вершины v 1 в вершину v 6. Пусть это будет путь  . Минимальную пропускную способность на этом пути, равную 10, имеет дуга
. Минимальную пропускную способность на этом пути, равную 10, имеет дуга  , т.е.
, т.е.  Увеличим на этом пути поток до 10 единиц. Дуга
Увеличим на этом пути поток до 10 единиц. Дуга  становится насыщенной. Дуга
становится насыщенной. Дуга  имеет на данный момент пропускную способность, равную 10.
имеет на данный момент пропускную способность, равную 10.
Путь  Следовательно, поток на этом пути можно увеличить на 9 единиц. Дуги
Следовательно, поток на этом пути можно увеличить на 9 единиц. Дуги  становятся насыщенными.
становятся насыщенными.
Других маршрутов нет (другие маршруты проходят через насыщенные дуги). Поток максимален. Делаем разрез вокруг вершины v 1 по насыщенным дугам


и получаем его величину  единиц.
единиц.
■
9. Используя алгоритм Краскала, построить остов с наименьшим
весом для неориентированного взвешенного графа  , у ко-торого
, у ко-торого  , если заданы веса (длины) ребер:
, если заданы веса (длины) ребер:

□ Построим граф G:

1. Упорядочим ребра в порядке неубывания веса (длины):


2. Возьмем ребро u 1 и поместим его в строящийся остов.
Возьмем ребро u 2 и поместим его в строящийся остов (т.к. оно не обра-зует с предыдущим ребром цикла).
Берем ребро u 3 и помещаеи его в строящийся остов (т.к. оно не образу-ет с предыдущими ребрами цикла).
Берем ребро u 4 и помещаем его в строящийся остов (т.к. оно не образу-ет с предыдущими ребрами цикла).
Берем ребро u 5 и помещаем его в строящийся остов (т.к. оно не образу-ет цикла с предыдущими ребрами).
Проверим окончание алгоритма. Число входящих в остов ребер равно 5. Заданный граф имеет п = 6 вершин и  . Таким образом, остов содержит все вершины заданного графа G.
. Таким образом, остов содержит все вершины заданного графа G.
Вес (длина) построенного остова

равен 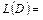
 .
.
■
- КОНТРОЛЬНЫЕ ВОПРОСЫ
- Действия над множествами. Кортеж. Декартово произведение.
- Диаграмма Эйлера – Венна.
- Алгебра множеств Кантора. Законы и свойства алгебры множеств.
- Соответствия.
- Функции. Отображения.
- Бинарное отношение порядка. Упорядоченные множества.
- Решетка. Дедекиндовые решетки. Дистрибутивные решетки.
- Правила суммы и произведения.
- Формулы расчета перестановок и сочетаний.
- Понятие метода включений и исключений.
- Понятие метода производящих функций.
- Независимое (внутренне устойчивое) множество. Число внутренней устойчивости графа. Алгоритм выделения пустых подграфов.
- Вершинное число внешней устойчивости графа.
- Плотность графа. Алгоритм выделения полных подграфов.
- Раскраска графов. Алгоритм минимальной раскраски графа.
- Определение кратчайших путей. Алгоритм Дейкстры.
- Максимальный поток через сеть. Алгоритм Форда – Фалкерсона.
- Построение остова экстремального веса. Алгоритм Краскала.
ЛИТЕРАТУРА
1. Богданов А.Е. Курс лекций по дисциплине «Дискретная математика».
- Северодонецк: ТИ ВНУ имени Владимира Даля, - 2012. – 195 с.
2. Горбатов В.А. Основы дискретной математики. – М.: Высшая школа,
1986. – 311 с.
3. Коршунов Ю.М. Математические основы кибернетики. – М.: Энерго-
атомиздат, 1987. – 496 с.
4. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для
инженера. – М.: Энергоатомиздат, 1988. – 480 с.
5. Шапорев С.Д. Дискретная математика. – СПб.: БХВ-Петербург, 2006.
- 400 с.
6. Гаврилов Г.П., Сапоженко А.А. Задачи и упражнения по дискретной
математике. – М.: ФИЗМАТЛИТ, 2005. – 416 с.
7. Богданов А.Е. Методические указания к практическим занатиям по
курсу “Дискретная математика” (элементы теории множеств), ч. 1. –
Северодонецк: СТИ, 1997. – 45 с.
8. Богданов А.Е. Методические указания к практическим занятиям по
курсу “Дискретная математика” (элементы теории множеств), ч. 2. –
Северодонецк: СТИ, 1997. – 35 с.
9. Богданов А.Е. Методические указания к практическим занятиям по
курсу “Дискретная математика” (элементы теории графов), ч. 1. –
Северодонецк: СТИ, 2000. – 44 с.
10.Богданов А.Е. Методические указания к практическим занятиям по
курсу “Дискретная математика” (элементы теории графов), ч. 2. –
Северодонецк: СТИ, 2001. – 49 с.
Учебное издание
МЕТОДИЧЕСКИЕ УКАЗАНИЯ






