МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К выполнению индивидуального задания
Контрольной работы) по дисциплине
“ДИСКРЕТНАЯ МАТЕМАТИКА “
для студентов дневной (заочной) формы обучения
направления подготовки 6.050102
“Компьютерная инженерия”
(электронное пособие)
Северодонецк 2012
УДК 519
Методические указания к выполнению индивидуального задания (контрольной работы) по дисциплине “Дискретная математика” для студентов дневной и заочной форм обучения направления подготовки 6.050102 “Компьютерная инженерия ” (электронное пособие) /Сост. А.Е.Богданов – Северодонецк: Изд-во ТИ ВНУ им. Владимира Даля, 2012. – 66 с.
Разработано на основании рабочей программы дисциплины «Дискретная математика»
| Составитель | ______________ | А. Е. Богданов, к.т.н., доц. | |
| Ответственный за выпуск | ______________ | О.В. Поркуян, зав.каф., д.т.н., проф. | |
| Рецензент | ______________ | А.И. Рязанцев, к.т.н., проф. |
Утверждено на заседании методической комиссии факультета КИ
Протокол № _ 5 _ от _ 03 _. _ 12 _. 2012 г.
Председатель комиссии М.И. Хиль, доцент, к.т.н.
ОГЛАВЛЕНИЕ
Введение…………………………………………………………………. 4
1. Варианты индивидуального задания (контрольной работы) ……. 6
2. Образец выполнения индивидуального задания
(контрольной работы) …………………………………………….. 43
3. Контрольные вопросы……………………………………………… 64
Литература………………………………………………………............ 65
ВВЕДЕНИЕ
Индивидуальное задание (контрольная работа) охватывает все основные разделы дисциплины “Дискретная математика”: “Теория множеств”, “Комбинаторный анализ”, “Графы”.
Цель методических указаний состоит в получении студентом практических навыков для закрепления теоретического материала дисциплины “Дискретная математика” [1].
Индивидуальное задание выполняют студенты дневной формы обучения; контрольную работу выполняют студенты заочной формы обучения.
В пункте 1 методических указаний представлены варианты индивидуального задания (контрольной работы). Номер варианта индивидуального задания (контрольной работы) соответствует порядковому номеру Ф.И.О. студента в академическом журнале группы.
Для решения задач индивидуального задания (контрольной работы) студент должен хорошо ориентироваться во всем курсе дисциплины “Дискретная математика”. Конкретно:
- для решения задач №№ 1 – 3 студент должен знать основные понятия теории множеств, алгебру множеств Кантора, диаграмму Эйлера – Венна, соответствия, функции, отображения, бинарное отношение порядка, упорядоченные множества, решетки ([1], Глава 1, §§ 1-3, 6, 7);
- для решения задач №№ 4 – 6 студент должен знать правила суммы и произведения, формулы расчета перестановок и сочетаний, метод включений и исключений, метод производящих функций ([1], Глава 2, §§ 2, 3, 5, 6);
- для решения задачи № 7 студент должен знать независимое (внутренне устойчивое) множество вершин графа, вершинное число внешней устойчивости графа, плотность графа, раскраску графа ([1], Глава 4, §§ 3-6);
- для решения задачи № 8 студент должен знать алгоритм Дейкстры определения кратчайших путей, алгоритм Форда – Фалкерсона определения максимального потока через сеть ([1], Глава 5, §§ 1, 2);
- для решения задачи № 9 студент должен знать алгоритм Краскала построения остова экстремального веса ([1], Глава 5, §§ 3).
В пункте 2 методических указаний показан образец решения и оформления индивидуального задания (контрольной работы).
В пункте 3 методических указаний представлены контрольные вопросы для защиты индивидуального задания (контрольной работы).
В конце методических указаний указана литература для изучения дисциплины “Дискретная математика” и выполнения индивидуального задания (контрольной работы).
Для получения удовлетворительной оценки за выполненное индивидуальное задание (контрольную работу) студент должен правильно решить 2/3 задач, представленных в индивидуальном задании (контрольной работе). После получения удовлетворительной (и выше) оценки за выполненное индивидуальное задание (контрольную работу) преподаватель назначает дату и время защиты индивидуального задания (контрольной работы). На защите студент должен объяснить решение какой-либо задачи (по усмотрению преподавателя) и ответить на один контрольный вопрос (по усмотрению преподавателя).
ВАРИАНТЫ ИНДИВИДУАЛЬНОГО ЗАДАНИЯ (КОНТРОЛЬНОЙ РАБОТЫ)
1. Представить с помощью кругов Эйлера множественное выражение. Используя законы и свойства алгебры множеств, упростить заданное выражение.
2. Заданы множества кортежей. Показать, что эти множества представляют собой соответствия между множествами N 1 и N 2, если N 1 = N 2 = 
. Дать полную характеристику этих соответствий.
3. Частично упорядоченное множество М задано множеством упорядо-ченных пар. Построить диаграмму и определить является ли данное множество решеткой. Если заданное множество является решеткой, то определить является ли решетка дедекиндовой, дистрибутивной.
4. Из колоды, содержащей 52 карты, вынули 10 карт. В скольких случаях среди этих карт окажется указанное количество указанных карт?
5. После обследования читательских вкусов оказалось, что 60% студентов читает журнал А, 65% − журнал В, 60% − журнал С, 55% − журнал Д, 40% − журналы А и В, 35% − журналы А и С, 30% − журналы А и Д, 40% − журналы В и С, 35% − журналы В и Д, 30% − журналы С и Д, 25% − журналы А, В и С, 20% − журналы А, В и Д, 20% − журналы А, С и Д, 15% − журналы В, С и Д, 10% − журналы А, В, С и Д. Сколько процентов студентов читает указанные журналы?
6. Решить рекуррентное соотношение.
7. Для неориентированного графа 
, у которого 
:
а) вычислить числа 
;
б) определить хроматическое число 
.
8. Для заданной сети 
:
а) найти величину минимального пути и сам путь от вершины 
до вершины 
по алгоритму Дейкстры;
б) используя алгоритм Форда-Фалкерсона, определить максималь-ный поток 
(v 1 – вход, v 7 – выход сети) и указать ми-нимальный разрез, отделяющий v 1 от v 7,
если задана матрица весов (длин, пропускных способностей) Р.
9. Используя алгоритм Краскала, построить остов с наименьшим весом для неориентированного взвешенного графа , у ко-торого 
, если заданы веса (длины) ребер.
ВАРИАНТ № 1
1. 
2. 
3. 
.
4. Хотя бы один «туз».
5. Не читает ни одного журнала.
6. 
7. 
.
v 1 v 2 v 3 v 4 v 5 v 6 v 7
8. Р = 
.
9. 
ВАРИАНТ № 2
1. 
2. 
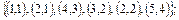
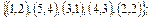
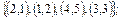
3. 
.
4. Ровно два «короля».
5. Читает только журнал А.
6. 
7. 
.
v 1 v 2 v 3 v 4 v 5 v 6 v 7
8. Р = 
.
9. 
ВАРИАНТ № 3
1. 
2. 
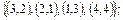
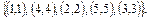
3. 
.
4. Не менее трех «дам».
5. Читает только журналы А и В.
6. 
7. 
.
v 1 v 2 v 3 v 4 v 5 v 6 v 7
8. Р = 
.
9. 
ВАРИАНТ № 4
1. 
2. 
3. 
.
4. Не более двух «валетов».
5. Читает только журналы А, В и С.
6. 
7. 
.
v 1 v 2 v 3 v 4 v 5 v 6 v 7
8. Р = 
.
9. 
ВАРИАНТ № 5
1. 
2. 
3. 
.
4. Ни одного «короля».
5. Читает только один журнал.
6. 
7. 
.
v 1 v 2 v 3 v 4 v 5 v 6 v 7
8. Р = 
.
9. 
ВАРИАНТ № 6
1. 
2. 
3. 
.
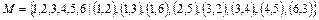4. Хотя бы два «туза».
5. Читает менее четырех журналов.
6. 
7. 
.
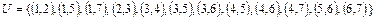v 1 v 2 v 3 v 4 v 5 v 6 v 7
8. Р = 
.
9. 
ВАРИАНТ № 7
1. 
2. 
3. 
.
4. Ровно четыре «туза».
5. Читает не менее двух журналов.
6. 
7. 
.
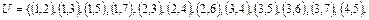
v 1 v 2 v 3 v 4 v 5 v 6 v 7
8. Р = 
.
9. 
ВАРИАНТ № 8
1. 
2. 
3. 
.
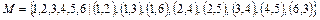4. Не менее одного «валета».
5. Читает не более одного журнала.
6. 
7. 
.
v 1 v 2 v 3 v 4 v 5 v 6 v 7
8. Р = 
.
9. 
ВАРИАНТ № 9
1. 
2. 
3. 
.
4. Не более трех «дам».
5. Читает только журнал В.
6. 
7. 
.
v 1 v 2 v 3 v 4 v 5 v 6 v 7
8. Р = 
.
9. 
ВАРИАНТ № 10
1. 
2. 
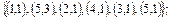
3. 
.
4. Ни одного «туза».
5. Читает только журналы А и С.
6. 
7. 
.
v 1 v 2 v 3 v 4 v 5 v 6 v 7
8. Р = 
.
9. 
ВАРИАНТ № 11
1. 
2. 
3. 
.
4. Хотя бы три «туза».
5. Читает только журналы А, В и Д.
6. 
7. 
.
v 1 v 2 v 3 v 4 v 5 v 6 v 7
8. Р =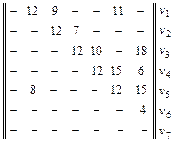 
.
9. 
ВАРИАНТ № 12
1. 
2. 
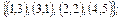
3. 
.
4. Ровно один «валет».
5. Читает только два журнала.
6. 
7. 
.
v 1 v 2 v 3 v 4 v 5 v 6 v 7
8. Р = 
.
9. 
ВАРИАНТ № 13
1. 
2. 
3. 
.
4. Не менее двух «дам».
5. Читает менее трех журналов.
6. 
7. 
.
v 1 v 2 v 3 v 4 v 5 v 6 v 7
8. Р = 
.
9. 
ВАРИАНТ № 14
1. 
2. 
3. 
.
4. Не более трех «королей».
5. Читает не менее трех журналов.
6. 
7. 
.
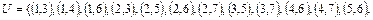
v 1 v 2 v 3 v 4 v 5 v 6 v 7
8. Р = 
.
9. 
ВАРИАНТ № 15
