2. 
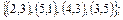
3. 
.
4. Ровно три «короля».
5. Читает не менее трех журналов.
6. 
7. 
.
v 1 v 2 v 3 v 4 v 5 v 6 v 7
8. Р = 
.
9. 
ОБРАЗЕЦ ВЫПОЛНЕНИЯ ИНДИВИДУАЛЬНОГО ЗАДАНИЯ (КОНТРОЛЬНОЙ РАБОТЫ)
1. Представить с помощью кругов Эйлера множественное
выражение
.
Используя законы и свойства алгебры множеств, упростить заданное выражение.
□ Используя круги Эйлера и, учитывая, что операция пересечения выполняется раньше операции объединения, получим следующие рисунки:
Объединяя заштрихованные области, получим искомое множество:
Упростим заданное выражение:
=
.
■
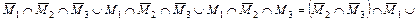
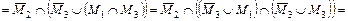
2. Заданы множества кортежей:
.
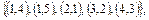
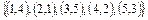Показать, что эти множества представляют собой соответствия между множествами N 1 и N 2, если N 1 = N 2 = 
. Дать полную характеристику этих соответствий.
□ Найдем декартово произведение:
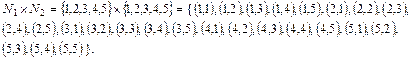
Видно, что заданные множества являются подмножествами этого прямого произведения. Следовательно, данные множества есть соответствия.
а) 
.
Область определения: 
. Следовательно, соответствие является частично определенным.
Область значений: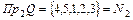 
. Следовательно, соответствие является сюръективным.
Образом элемента 
являются два элемента 
. Значит, соответствие не является функциональным. Из этого следует, что соответствие не является функцией, отображением.
б) 
.
Область определения: 
. Следовательно, соответствие является частично определенным.
Область значений: 
. Следовательно, соответствие не является сюръективным.
Образом любого элемента из 
является единственный элемент из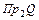 
. Следовательно, соответствие является функциональным, функцией. Соответствие является частично определенным. Это означает, что функция является частично определенной и не является отображением.
в) 
.
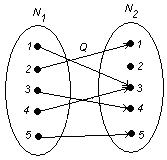
Область определения: 
. Следовательно, соответствие всюду определено.
Область значений: 
. Следовательно, соответствие не является сюръективным.
Образом любого элемента из является единственный элемент из 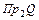. Следовательно, соответствие является функциональным, функцией. Так как соответствие всюду определено, то имеем полностью определенную функцию, т.е. имеем отображение N 1 в N 2.
г) 
.
Область определения: . Значит, соответствие полностью определено.
Область значений: 
. Значит, соответствие сюръективно.
Образом любого элемента из N 1 является единственный элемент из N 2. Следовательно, соответствие является функциональным, функцией.
Так как соответствие всюду определено, сюръективно, функционально и прообразом любого элемента из 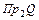является единственный элемент из , то соответствие является взаимно однозначным.
Так как функция полностью определена и соответствие сюръективно, то имеем отображение N 1 на N 2.
Так как для любых двух различных элементов из N 1 их образы из N 2 также различны, то отображение является инъективным.
Так как отображение является одновременно сюръективным и инъективным, то имеем биективное отображение (взаимно однозначное отображение).
■
3. Частично упорядоченное множество М задано множеством
упорядоченных пар
.
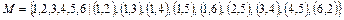Построить диаграмму и определить, является ли данное множество решеткой. Если заданное множество является решеткой, то определить, является ли решетка дедекиндовой, дистрибутивной.
□ Построим диаграмму:
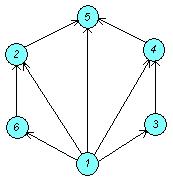
Построим таблицу:
| Пары элементов | Н.Г. | В.Г. | Н.Н.Г. | Н.В.Г. |
| 1,2 | 2,5 | |||
| 1,3 | 3,4,5 | |||
| 1,4 | 4,5 | |||
| 1,5 | ||||
| 1,6 | 6,2,5 | |||
| 2,3 | ||||
| 2,4 | ||||
| 2,5 | 2,6,1 | |||
| 2,6 | 6,1 | 2,5 | ||
| 3,4 | 3,1 | 4,5 | ||
| 3,5 | 3,1 | |||
| 3,6 | ||||
| 4,5 | 4,3,1 | |||
| 4,6 | ||||
| 5,6 | 6,1 |
Так как любая пара элементов имеет единственную наибольшую ниж-нюю грань и единственную наименьшую верхнюю грань, то заданное частично упорядоченное множество М является решеткой.
Решетка М является дедекиндовой, когда выполняется равенство:
для таких 
, что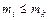 
.
Решетка М не является дедекиндовой, т.к. указанное равенство не выполняется, например, для элементов 2, 3, 4:
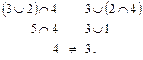
Одним из условий дистрибутивности решетки является ее дедекиндо-вость. Так как решетка М не является дедекиндовой, то она не является дистрибутивной решеткой.
■
4. Из колоды, содержащей 52 карты, вынули 10 карт. В скольких
случаях среди этих карт окажется не более одной «шестерки»?
□ Не более одной «шестерки» означает, что среди извлеченных 10 карт может быть: либо ни одной «шестерки», либо одна «шестерка». Всего в колоде 4 «шестерки».
По правилу произведения:
− ровно нуль «шестерок» (
− нуль «шестерок» из четырех и 
− десять не «шестерок» из 48 карт, не содержащих «шестерок»);
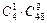− ровно одна «шестерка» (
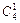− одна «шестерка» из четырех и 
− девять не «шестерок» из 48 карт, не содержащих «шестерок»).
Число не более одной «шестерки» среди выбранных 10 карт по правилу суммы будет равно
+ = 
=
= 
=
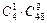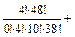
= 47·46·44·43·41·39 + 16·47·46·22·43·41·5 = 6 540 715 896 + 6 708 426 560 =
= 13 249 142 456
■
5. При опросе сотрудников некоторого учреждения оказалось, что 60% сотрудников знают английский язык, 50% − французский, 50% − немецкий, 30% − английский и французский, 20% − французский и немецкий, 40% − английский и немецкий, 10% − английский, французский и немецкий. Сколько процентов сотрудников знают не менее двух языков.
□ Знать не менее двух языков – это знать два или три языка. Пусть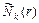 
− количество сотрудников, знающих не менее r языков из k языков. Тогда 
= 
+ 
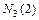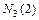, где − количество сотрудников, знающих два языка; − количество сотрудников, знающих три языка. Количество сотрудников, знающих два языка, можно определить по формуле
,
т.е.
= 
+ 
,
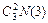где 
− количество сотрудников, знающих хотя бы два языка; 
− количество сотрудников, знающих три языка.
Пусть общее число сотрудников равно 1 или 100%. Тогда
= 0,3 + 0,2 + 0,4 = 0,9 и = 0,1 (по условию).
Следовательно,
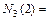1·0,9 − 3·0,1 = 0,6 или 60%.
По условию задачи = 0,1. Следовательно, количество сотрудников, знающих не менее 2 языков из 3 языков:
= 0,6 + 0,1 = 0,7 или 70%.
Для подсчета числа сотрудников, знающих не менее 2 языков, можно также воспользоваться формуле
= 
= 
= 
− 
=
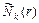= 1·0,9 − 2·0,1 = 0,2 или 70%.
■
6. Решить рекуррентное соотношение
□ Решить рекуррентное соотношение – это значит найти общий член последовательности 
, удовлетворяющей указанному рекуррентному соотношению.
Умножим заданное рекуррентное соотношение 
и просуммируем полученное выражение от нуля до бесконечности. В результате получим
или
,
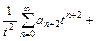
или
.
Так как 
= 
, то
, 
, 
.
Тогда
) 
) − 
,
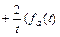
+ 9 t + 2 t − 8 t 2 = 
.
Отсюда
= 
= 
.
Методом неопределенных коэффициентов находим А, В и С:
,
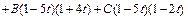пусть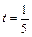 
: 
, А = 1;
пусть 
: 
, В = −3;
пусть 
: 
, С = 2.
Тогда
= 
=
= 
= 
.
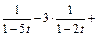
Следовательно, общий член 
последовательности 
имеет вид
= 
.
■
7. Для неориентированного графа 
, у которого 
, 
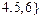а) вычислить числа 
;
б) определить хроматическое число 
.
□ Построим граф:
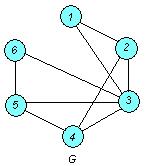
а) Вычислим числа 
.
1) 
:
Используя алгоритм выделения пустых подграфов, построим дерево:
Согласно определению :
.
2) 
:
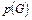Используя алгоритм выделения полных подграфов, построим дерево:
Здесь 
- полные подграфы. Видно, что мощность носителей всех под-графов равна трем, т.е.
.
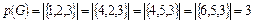3) 
:
Построим модифицированную матрицу смежности 
заданного графа G:
1 2 3 4 5 6
.
Находим минимальное число строк, покрывающих все столбцы модифи-цированной матрицы. Таких строк – одна. Следовательно,
.
б) Определим хроматическое число .
Согласно алгоритму минимальной раскраски вершин графа, выделим все пустые подграфы графа G, т.е. построим дерево (оно построено в пункте а)):
Построим таблицу:
1 2 3 4 5 6
1. {1,4,6} 1 1 1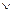 
2. {1,5} 1 1
3. {2,5} 1 1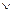
4. {2,6} 1 1
5. {3} 1
Определяем минимальное число строк, покрывающих все столбцы табли-цы. Такими строками могут быть строки 1, 3, 5. Значит,
.
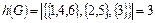Зададимся красками: для множества вершин 
- краска синяя (С), для множества вершин 
- краска красная (К), для множества вер-шин 
- краска зеленая (З).
Раскрасим вершины графа G:
■
8. Для заданной сети 
:
а) найти величину минимального пути и сам путь от вершины 
до вершины 
по алгоритму Дейкстры;
б) используя алгоритм Форда-Фалкерсона, определить максималь-ный поток 
(v 1 – вход, v 6 – выход сети) и указать ми-нимальный разрез, отделяющий v 1 от v 6,
