Часові лінії.
Грошові суми у фінансових операціях і комерційних справах завжди позв'язані з конкретними моментами часу. У договорах і контрактах фіксуються терміни і періодичність надходження коштів або виплат. Тому при відпрацюванні управлінських рішень в області фінансів менеджер повинний постійно порівнювати минулі, теперішні і майбутні витрати і доходи. Суть порівняння складається в нерівноцінності однієї і тієї ж суми в різні моменти часу. Метод порівняння полягає у встановленні взаємозв'язку часу і коштів.
В основі концепції тимчасової вартості грошей лежить наступний основний принцип: сьогоднішня грошова одиниця дорожче «завтрашньої» не тільки тому, що інфляція знижує її купівельну спроможність, але і тому, що інвестована сьогодні грошова одиниця завтра принесе конкретний прибуток. Суть концепції полягає в тім, що вартість грошей з часом змінюється з урахуванням визначеної ставки прибутковості.
Одним з найважливіших інструментів проведення аналізу тимчасової вартості грошей є часова лінія, якою користуються для досягнення наочності проблеми і для того, як її можна вирішити.
Для ілюстрації концепції часової лінії розглянемо наступну діаграму:
Час 0 1 2 3 4 5
___________________________________________________
Час 0 – це сьогоднішній день; час 1 – один період з сьогоднішнього дня або закінчення цього періоду; час 2 – два періоди з сьогоднішнього дня або закінчення цього періоду і т.д. Таким чином, цифри над штрихами над часовою лінією показують на закінчення певних часових періодів. Найчастіше ці періоди є роками, але можуть бути представлені і півріччями, і кварталами, і місяцями і навіть днями. Слід мати на увазі, що кожен штрих на лінії відзначає кінець одного періоду і у той же час є початком наступного. Наприклад, штрих 1 означає кінець року 1 і початок 2.
Показники потоку готівки розташовуються точно під показниками років, а показники відсоткових ставок – над часовою лінією між часовими інтервалами. Невідомий показник потоку готівки, який необхідно визначити, вказується на лінії знаком питання.
Час 0 5% 1 2 3
_______________________________
Потік готівки - 100?
У даному випадку відсоткова ставка для всіх трьох періодів становить 5%. Під час 0 відбувся одноразовий відплив потоку готівки, під час 3 очікується невідомий приплив готівки. Показник відпливу готівки відзначається знаком мінус. Показник періоду 3 знака мінус не має. Зверніть увагу, що в періоди 1 і 2 у потоці готівки не було ніяких змін. На часовій лінії найменування грошової одиниці не вказується, що дозволяє уникнути плутанини.
Тепер розглянемо таку ситуацію: відплив готівки у 100 грошових одиниць має місце сьогодні, і ми очікуємо невідому суму наприкінці періоду 2:
Час 0 5% 1 10% 2
_____________________
Потік готівки - 100?
У цьому випадку відсоткова ставка в перший період становить 5%, але протягом другого періоду вона виросте до 10%. Якщо відсоткова ставка постійна у всі періоди, її вказують тільки для першого періоду, якщо вона змінюється – її вказують для кожного періоду окремо.
Часові лінії дуже важливі для початкового розуміння концепції тимчасової вартості грошей, але навіть досвідчені спеціалісти користуються нею для проведення складного аналізу проблем.
Майбутня вартість грошей. Розрахунок нарощених сум по простих і складних відсоткових ставках. Процеси компаундировання.
У процесі порівняння вартості коштів при їхньому інвестуванні і поверненні прийнято використовувати два основних поняття: майбутня вартість грошей і їхня теперішня (поточна) вартість.
Майбутня вартість являє собою суму інвестованих у даний момент коштів, у яку вони перетворяться через визначений період часу з урахуванням визначеної ставки відсотка.
Визначення майбутньої вартості (FV) грошей пов'язано з процесом нарощення цієї вартості, що являє собою поетапне збільшення вихідної суми шляхом приєднання до її первісного капіталу відсоткових платежів. Ця сума розраховується по так званій відсотковій ставці, що характеризує прибутковість кредитної угоди. Вона показує, яка частка від суми виданого кредиту буде повернута власнику капіталу у виді доходу. Тому відсоткова ставка (r), що виражена десятковим дробом, розраховується як відношення доходу (I), отриманого за визначений період (n) часу (найчастіше за рік), до величини капіталу, наданого в кредит (PV):
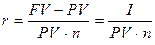(4.1)
У процесі нарощення відсоткові ставки за способом нарахування є декурсивними або послідовними, тобто відсотковий платіж нараховується наприкінці кожного розрахункового року.
Величину I часто називають відсотковими грошима, відсотковим доходом або просто відсотками.
При проведенні фінансово-економічних розрахунків, що позв'язані з інвестуванням коштів, процеси нарощення і дисконтування можуть здійснюватися як по простих, так і по складних відсотках. Прості відсотки застосовуються, як правило, при короткостроковому інвестуванні, а складні відсотки – при довгостроковому.
Простим відсотком називається сума, що нараховується по первісній (теперішньої) вартості внеску наприкінці одного періоду платежу, зумовленого умовами інвестування (місяць, квартал, півріччя, рік і т.д.)
При розрахунку суми простого відсотка, тобто доходу на вкладений капітал, у процесі нарощення внеску використовуються наступні формули:
I = FV – PV (4.2)
(4.3)
(4.4)
У формулі (4.3) відсоткова ставка виражена десятковим дробом, а у формулі (4.4) – у відсотках.
Виходячи з формул (4.2) і (4.3) можна сказати, що нарощена сума (або майбутня вартість, FV) є результат додавання суми, наданої в кредит і відсоткових грошей. Операція визначення нарощеної суми називається компаундингом.
Формула для визначення нарощеної суми з використанням простих відсотків виглядає таким чином:
(4.5)
Вираз (1+nr) називається множником або коефіцієнтом нарощення простих відсотків(кн). Його значення завжди повинне бути > 1:
(4.6)
У ряді випадків при розробці умов контрактів або їх аналізі виникає задача визначення терміну позички. При використанні простої ставки відсотка тривалість терміну позички (n) дорівнює:
(4.7)
На практиці зустрічаються випадки, коли кошти розміщуються не на рік, а на точно визначену кількість днів. Тоді,
(4.8)
у днях 
, (4.9)
де h – інвестування в днях;
К – кількість днів у році (часова база для розрахунку відсотків).
Величина процентної ставки для h днів визначається:
(4.10)
У такому випадку нарощена сума дорівнює:
; коефіцієнт нарощення: 
(4.11)
У залежності від визначення K і h застосовують наступні методики:
1. Точні відсотки з точним числом днів між датою видачі кредиту, розміщення депозиту і датою повернення кредиту. Точна кількість днів визначається по календарю або по спеціальних таблицях. При цьому день видачі кредиту і його повернення вважається як один день. Наприклад, позичка видана з 3 січня по 12 березня. Точне число днів по календарю:
h = 29 + 28 + 12 – 1 = 68
Точна кількість днів за допомогою спеціальних таблиць можна визначити по формулі:
h = hп - hв, (4.12)
де hп - дата погашення позики;
hв - дата видачі позики.
Число днів у році К = 365 або 366 для високосного року.
Цей метод використовується в Португалії, Англії, США, тому його називають «англійською практикою». Цей метод вигідний для боржників.
2. Банківський метод, при якому h визначається знову як точна кількість днів. Число днів у році приймається К = 360. Метод дає фінансові переваги банкам при видачі кредиту на термін більш 360 днів. Відсотки при цьому методі називаються комерційними. Використовують цей метод у Франції, Бельгії, Іспанії, Швейцарії, називають його «французькою практикою». Для інвестора це самий вигідний метод.
3. Звичайні відсотки з наближеним числом днів. У цьому методі число днів у місяці приймається за 30, а К = 360 і в приведеному прикладі
h = 28 + 30 + 12 – 1 = 69
Цей метод використовують у Німеччині, Данії, Швеції, тому його називають «німецькою практикою». Застосовується метод при частковому погашенні позички.
При складанні кредитної угоди може бути встановлена постійна на весь період відсоткова ставка, або така що змінюється (перемінна).
При встановленні перемінної відсоткової ставки нарощена сума визначається по формулі:
(4.13)
де r – ставка простих відсотків у період t;
nt – тривалість нарахування ставки it;
m – число періодів нарахування відсотків.
Поряд з розглянутим методом нарахування по простій відсотковій ставці використовується метод нарахування по складній відсотковій ставці. Суть методу полягає в тім, що на нарощені в попередньому періоді суми знову нараховуються відсотки, тобто сума нарахованого простого відсотка не виплачується після кожного періоду, а приєднується до суми основного внеску і у наступні періоди сама приносить доход. Подібний процес називається капіталізацією доходу.
Нарощена (майбутня) вартість по складних відсотках визначається по формулі:
(4.14)
Множник 
називається множником нарощення складних відсотків. У зарубіжній практиці множник позначають аббревиатурою FVIF (r, n), його значення табулировані. Тепер формула (4.13) прийме вид:
FV = PV х FVIF (r, n) (4.15)
Для того, щоб краще зрозуміти процес нарощення слід звернутися до часової лінії.
0 r =5% 1 2 3 4 5
__________________________________________________
х 1,05 х 1,05 х 1,05 х 1,05 х 1,05
Початковий внесок - 100 (PV) FV1-? FV2-? FV3-? FV4-? FV5-?
Нарахований
відсоток (I) 5,00 5,25 5,51 5,79 6,08
Сума на кінець
кожного періоду (FV) 105,00 110,25 115,76 121,55 127,63
Використання у фінансових обчисленнях простих і складних відсоткових ставок дає неоднакові результати, розходження між ними обумовлені термінами угод.
При рівній величині простих і складних відсоткових ставок (rп=rс) при терміну позички менш одного року (n<1) нарощена сума, нарахована по простих відсотках, буде більше нарощеної суми, обчисленої по складних відсотках.
Найчастіше банки, надаючи довгострокові кредити, використовують ставки складних відсотків, що змінюються в часі, але заздалегідь фіксовані для кожного періоду. У цьому випадку нарощена сума визначається по формулі:
(4.16)
де r1, r2,…r12 -послідовні значення ставок відсотків;
n1, n2 ,…nk -періоди, протягом яких використовуються відповідні ставки.
Якщо термін угоди більше року (n>1), нарощення по складних відсотках випереджає нарощення по простих відсотках (1+n).
Якщо термін фінансової угоди виражений дробовим числом, нарахування відсотків може виконуватися двома способами:
а) по формулі складних відсотків
(4.17)
б) комбінованим методом
(4.18)
де n = a + b – період угоди;
а – ціле число років;
b – дробова частина року (b=b /360, або 365, 366).
У контрактах на одержання кредитів часто передбачається нарахування відсотків кілька разів на рік – по півріччях, кварталах, іноді щомісячно і щодня.
Однак на практиці, у більшості випадків, вказується не квартальна чи місячна відсоткова ставка, а річна ставка, що називається номінальною (j). Крім того, вказується число періодів (m) нарахування відсотків на рік. Тоді нарощена сума грошей (FV) за період (n) обчислюється по формулі:
, (4.19)
де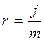 
- ставка за один період нарахування;
n = mn – загальна тривалість терміну інвестування.
Нарощена сума при нарахуванні відсотків:
а) один раз у рік (при m= 1 і r= 100%):
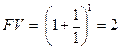
б) по півріччях (при m= 2 і r= 100%):
в) по кварталах (при m= 4 і r= 100%):
г) щомісяця (при m= 12 і r= 100%):
Розрахунок показує, що чим більше періодів нарахування відсотків, тим більше вигідно це клієнту банку. Зі збільшенням загального інтервалу часу складні відсотки наростають швидше, отже, буде збільшуватися і абсолютний річний прибуток. Реальна прибутковість чи, іншими словами – норма прибутку інвестицій, виражається річною ефективною процентною ставкою.
Річна ставка складних відсотків, еквівалентна номінальної при нарахуванні відсотків m разів на рік, називається ефективною ставкою і позначається r або re.
Річна ефективна ставка (r) пов'язана з річною номінальною ставкою (j) співвідношенням, що випливає із порівняння правих частин формул (4.14) і (4.19)
.
Звідси
, (4.20)
тобто ефективна ставка більше номінальної. З цього виразу випливає, що
j = m [(1 + re)1/m – 1] (4.21)
Існує кілька правил, що дозволяють швидко розрахувати термін подвоєння первісної суми для конкретної відсоткової ставки (тільки по складних відсотках!)
Правило "72". Для визначення терміну, за котрий відбудеться подвоєння капіталу, необхідно число 72 поділити на відому ставку:
n = 72/r, (4.22)
де n – період подвоєння;
r - ставка.
Правило "69". Термін, за котрий відбудеться подвоєння капіталу, розраховується по наступній формулі:
n = 69/r + 0,35, (4.23)
Дані правила дають дуже точний результат при значеннях
r £ 100%, а вище – вже погрішності.
