Формула А.И. Целикова:
,
где 
;
при 
;
;
при 
(см. рис. IV.7);
при 
;
при 
;
при 
;
,
где коэффициент g учитывает влияние s2; nb– изменение влияния внешнего трения в связи с уширением; ns– влияние напряжённого состояния; n¢s– влияние внешнего трения; n¢¢s– влияние внешних зон; n¢¢¢s– влияние натяжения; nsб–влияние боковых внешних зон; S и S0– площади поперечного сечения полосы и её обжимаемой части.
Формула А.А. Королёва [22]:
;
;
; 
;
; при 
; 
,
где 
– коэффициент, характеризующий наличие зон скольжения и прилипания; 
– протяжённость зоны прилипания.
Формула В.С. Смирнова [4]:
;
при 
;
при 
;
;
При наличии одной зоны прилипания, т.е. при 
или при 
,
; 
.
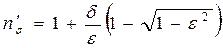При наличии зон скольжения
; 
,
где n¢s– коэффициент, учитывающий влияние контактного трения и натяжения; 
– коэффициент трения при установившемся процессе прокатки;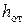 
, 
– толщина полосы на границах зон отставания и опережения.
Формула Экелунда [37]:
,
где 
;
;
;
,
где 
– коэффициент, учитывающий внешнее трение; 
– сопротивление деформации при статическом сжатии; 
– коэффициент вязкости металла; 
– коэффициент, зависящий от скорости деформирования 
. При , равном 6;10;15 и 20м/c, коэффициент соответственно равен 1;0,8;0,65 и 0,6; 
– скорость деформации, с-1; 
– содержание углерода, марганца и хрома в металле, %.
Формула С.И. Губкина [21]:
,
где 
;
,
где 
– скоростной коэффициент, при 
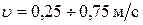
; при 
; при 
; 
– температурный коэффициент (верхний предел принимают для твёрдых растворов с большой концентрацией); 
– температура плавления °С;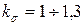 
– коэффициент неравномерности распределения температурных напряжений; 
– временное сопротивление, соответствующее температуре 
и скорости деформирования 
[57]; 
– коэффициент трения.
Формула Гелеи [2]:
,
где 
– сопротивление линейной деформации, 
– для нелегированных углеродистых сталей; 
– для высокоуглеродистых сталей; содержащих 
и 
; 
– коэффициент, зависящий от 
(см. рис. IV.10); – окружная скорость валков, 
.
Формула А.П. Чекмарёва [28]:
,
где 
,
– коэффициент формы калибра; П–периметр калибра; b– ширина калибра по разъёму; 
см. формулу А.И. Целикова; b– коэффициент Лодэ.
Значение коэффициента формы для различных калибров [28]:
Квадратный…………………………………………………….1,41
Ромбический, с углом при вершине, град:
100……………………………………………………1,30
110……………………………………………………1,20
120……………………………………………………1,15
Круглый………………………………………………………..1,40
Овальный однорадиусный с 
, равном:
1,5…………………………………………………….1,27
2………………………………………………………1,15
3………………………………………………………1,09
Овальный плоский…………………………………………..1,1–1,15
Шестигранный…………………………………………………1,15
Угловой и зетовый:
чистовые……………………………………………...1,41
черновые……………………………………………1,2–1,25
Калибры двутавровой балки:
№30………………………………………………….1,7–1,9
№16………………………………………………….2,1–2,2
Калибры швеллера:
№30………………………………………………….1,7–1,8
№16………………………………………………….1,8–2,0
№8………………………………………………….…2,1–2,3
Рельс Р–50……………………………………………………..2–2,1
Шпунт Л–5…………………………………………………….1,8–2,1
Формула Е.С. Рокотяна [2]:
,
где 
– удельный расход энергии за данный проход с вычетом расхода энергии на трение в механизме прокатного стана, 
; 
–плотность металла, 
.
Формула А.А. Королёва [22]:
,
где 
при 
,
где 
– коэффициент напряжённого состояния при прокатке в калибрах; a и b– коэффициенты, зависящие от формы калибра, 
и 
, когда имеет место прокатка простых профилей (узкая полоса, плоский овал).
Схема деформации соответствует плоской (двухмерной): 
и 
для овальных и круглых калибров; 
и 
для квадратных и ромбических калибров,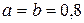 
для фасонных закрытых калибров.
При 
величина 
.
