Направления течения металла при прокатке показаны на рис. 55. В очаге деформации можно отметить четыре основные зоны течения металла: зона I – направление движения частиц металла совпадает с направлением прокатки, причём скорость их больше, чем скорость валков (опережение); зона II – движение частиц металла противоположно направлению прокатки со скоростью, меньшей, чем скорость валков (отставание); зоны III и IV – наблюдается течение металла в поперечном направлении (зоны уширения).
 |
Границей между зонами I и II, т.е. между зонами опережения и отставания, является линия EF,которая считается горизонтальной проекцией так называемого нейтрального сечения, в котором горизонтальная скорость течения металла
 и валков
и валков  равны между собой.
равны между собой.
Рис. 55. Направления течения металла при прокатке
Ниже рассмотрены методы количественного определения опережения и отставания частиц металла в очаге деформации без разбора теоретических вопросов кинематики процесса прокатки, которые подробно изложены в работах [31, 37, 62].
Наибольшее различие между скоростями металла и валков наблюдается на входе в очаг деформации. В нейтральном сечении скорости металла и валков равны. По мере продвижения металла к выходу из очага деформации, после прохождения нейтрального сечения, частицы металла перемещаются со скоростью большей, чем скорость вращения валков:
 (32-IV)
(32-IV)
где  – скорость выхода металла из очага деформации;
– скорость выхода металла из очага деформации;
 – окружная скорость валков;
– окружная скорость валков;
 – скорость металла при захвате его валками.
– скорость металла при захвате его валками.
Формулы по кинематике процесса прокатки
Таблица 27
| Номер формулы | Формулы | Источник | Обозначения и примечания |
| (33-IV) | 
| – |  – окружная скорость валков, – окружная скорость валков, 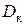 – катающий диаметр валка; – катающий диаметр валка;  – число оборотов валков – число оборотов валков
|
| (34-IV) | 
| – |  – горизонтальная проекция скорости частиц металла в критическом сечении – горизонтальная проекция скорости частиц металла в критическом сечении
|
| (35-IV) | 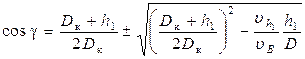 Это уравнение даёт возможность рассчитать величину критического угла g, по величине опережения S;
Это уравнение даёт возможность рассчитать величину критического угла g, по величине опережения S;

| [62] | g– критический угол;
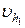 – скорость полосы при выходе из очага деформации; – скорость полосы при выходе из очага деформации;
 – толщина полосы после прокатки. Критический угол g определяют по формуле (10-IV), приведённой в табл. 20 – толщина полосы после прокатки. Критический угол g определяют по формуле (10-IV), приведённой в табл. 20
|
| (36-IV) | 
| [62] | m– коэффициент вытяжки;  и и  – площадь сечения полосы до и после прокатки; – площадь сечения полосы до и после прокатки; 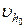 и и 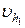 – скорость полосы при входе и выходе из валков – скорость полосы при входе и выходе из валков
|
| (37-IV) | 
| [62] | 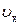 – скорость течения металла в любом сечении очага деформации, d – произвольный угол захвата – скорость течения металла в любом сечении очага деформации, d – произвольный угол захвата
|
| (38-IV) (39-IV) (40-IV) | 


| [62] [62] | S– опережение;  , ,  – расстояние между отпечатками на полосе и на валке;
a=13×10-6– коэффициент теплового расширения стали – расстояние между отпечатками на полосе и на валке;
a=13×10-6– коэффициент теплового расширения стали
|
| (41-IV) | 

| [37] |  – коэффициент опережения; – коэффициент опережения;  – коэффициент отставания – коэффициент отставания
|
| (42-IV) | 
| [62] | Справедливо для зоны опережения;  и и  – составляющие скорости валков и металла – составляющие скорости валков и металла
|
| (43-IV) | 
| [62] | Справедливо для зоны отставания |
| (44-IV) | 
| [62] | Используют при определении чисел оборотов валков непрерывных станов |
| (45-IV) | 
| – |  – скольжение в первой зоне очага деформации – скольжение в первой зоне очага деформации
|
| (46-IV) | 
| [37] |  – отставание – отставание
|
| (47-IV) | 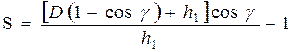
| [31] | Уравнение Финка |
| (48-IV) | 
| [31] | Уравнение А.И. Целикова |
| (49-IV) | 
| – | Уравнение Дрездена, или упрощённое уравнение Финка. Пригодна для случая прокатки тонких полос, когда  значительно больше значительно больше 
|
| (50-IV) | 
| – | Уравнение Иг.М. Павлова, где  – коэффициент зависящий от – коэффициент зависящий от  и и  . Значение этого коэффициента приведены в работе [35] с. 381 . Значение этого коэффициента приведены в работе [35] с. 381
|
| (51-IV) | 
| [63] | Уравнение Б.П. Бахтинова для определения опережения с учётом уширения |
| (52-IV) | 
| [64] | Формула Финка, преобразованная М.М. Штерновым |
| (53-IV) | 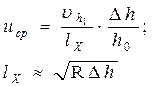
| [30] | Уравнения скорости деформации, полученное А.И. Целиковым |
| Условия непрерывной прокатки | |||
| (54-IV) (55-IV) (56-IV) (57-IV) | 



| [59] [37] – |  – постоянная калибровки
Прокатка с учётом натяжения полосы между клетями
m – коэффициент вытяжки в клети – постоянная калибровки
Прокатка с учётом натяжения полосы между клетями
m – коэффициент вытяжки в клети
|






