Метод основан на принципе суперпозиции, обусловленным линейностью электрической цепи. Если линейная цепь подвергается воздействию одновременно нескольких источников, то реакция цепи равна сумме реакций на каждое воздействие отдельно. Тогда принцип наложения можно сформулировать следующим образом: ток в любой ветви ЭЦ равен сумме токов, обусловленных в отдельности каждым источником, действующим в отсутствии остальных; напряжение между двумя точками ветви равно сумме напряжений, обусловленных в отдельности каждым источником, действующим в отсутствии остальных.
4.1. Алгоритм расчета тока в k -той ветви (напряжения между точками «а» - «б» в k -той ветви).
I. Получают столько L частичных схем, сколько в исходной схеме ЭЦ источников (ИИН и ИИТ).
II. В каждой частичной схеме оставляют один источник, заменяя остальные их внутренними сопротивлениями [0 для ИИН, ∞ (разрыв) для ИИТ].
III. Рассчитывается ток k -той ветви - Ikl (напряжение Uабkl в k -той ветви) каждой l- ной частичной схемы.
IV. Рассчитывается ток k -той ветви - Ik (напряжение Uабk в k -той ветви):
Ik = 
. Uабk = 
, руководствуясь правилом знаков – если направления токов (напряжений) в полной и частичной схеме совпадают, то токи (напряжения) берутся со знаком «+», если не совпадают – со знаком «-».
Пример 4
Рассчитать ток ветви а-б схемы рис.4 методом наложения.
Дано:
| Е1, В | J, А | R1, Ом | R2, Ом | R3, Ом | R4, Ом |
| 0,2 |
Расчет.
Поскольку исходная схема содержит два источника, ток Iх будет определяться как суперпозиция токов Iх = Iх` ± Iх`` ветви а-б двух частичных схем (рис. 5 и рис.6).
I. Расчет тока Iх` осуществляется с использование правила делителя тока, так как ток J разветвляется по двум ветвям:
Iх` = 
.
II. Для расчета тока Iх`` можно воспользоваться методом узловых потенциалов при условии, что потенциал точки «в» равен нулю, тогда ток
Iх`= 
.
Согласно МУП потенциал φа определяется из уравнения
Подставив числовые значения получаем:
Iх = Iх` ± Iх``= 0,34 А
Пример 5
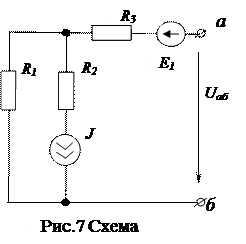
Рассчитать напряжение Uаб схемы рис.7 методом наложения.
Дано:
| Е1, В | J, А | R1, Ом | R2, Ом | R3, Ом |
| 0,2 |
Расчет:
Поскольку исходная схема содержит два источника, напряжение Uаб будет определяться как суперпозиция напряжений Uаб = Uаб ` ± Uаб ``для двух частичных схем (рис.8 и рис.9).
Очевидно, что напряжение Uаб `= - Е1, поскольку источник Е1 работает в режиме Х.Х. и точка «а» имеет отрицательный потенциал.
Напряжение
Uаб ``= - J R1 = -10 В.
Таким образом, напряжение Uаб= -60В.
5. Метод эквивалентного генератора
Метод применяется в том случае, когда необходимо рассчитать ток какой-либо ветви сложной схемы. Ветвь с искомым током IX (рис.10) представляется нагрузкой активного двухполюсника (АД), который заменяет собой всю остальную схему ЭЦ. АД в свою очередь реализуется в виде реального источника напряжения (РИН), величина ЭДС которого равна напряжению холостого хода на зажимах 1-2 АД, а внутреннее сопротивление - входному сопротивлению этого АД. Напряжение холостого хода можно рассчитать любым из известных методов расчета схемы ЭЦ, для расчета же входного сопротивления необходимо превратить АД в пассивный двухполюсник, для чего заменить в нем идеальные источники энергии их внутренними сопротивлениями (ИИН - 0; ИИТ - ∞).
Пример 6
Рассчитать ток ветви 2-4 схемы рис.11 используя метод эквивалентного генератора (ЭГ).
Дано:
| Е1, В | Е2, В | J, А | R1, Ом | R2, Ом | R3, Ом | R4, Ом | R5, Ом |
| 0,2 |
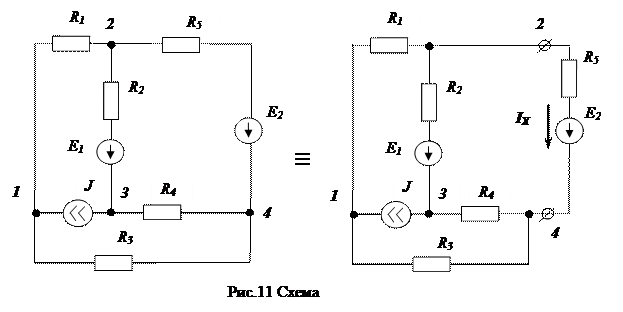
Расчет.
Расчет параметров ЭГ.
Расчет внутреннего сопротивления ЭГ производится по схеме рис.12, как входного сопротивления относительно зажимов 2-4 пассивного двухполюсника:
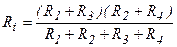= 73,3 Ом.
Для расчета напряжения холостого хода целесообразно использовать метод наложения. Согласно методу - U24 = U24 ` ± U24 ``, где U24 `- напряжение между точками 2-4 первой частичной схемы, U24 ``- напряжение между точками 2-4 второй частичной схемы. Для контура обхода схемы рис.13 имеет место следующее равенство: U24` - I(R2+R4)+E1= 0, где ток I =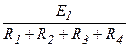 
. U24` = =I(R2+R4)-E1 = -16,6 В, Для контура обхода схемы рис.14 можно записать: U24`` + I2R4 – I1R2 = 0, откуда = I1R2 - I2R4 = Токи I1 и I2 определяются по правилу деления тока источника J:
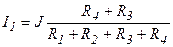= 0,079 А 
= 0,12 А.
U24`` = 3,45 В. Итак, UXXЭГ = U24. = -13,15 В. Следует обратить внимание на то, что ЭДС ЭГ (ЕЭГ) направлено от точки 2 к точке 4, т.к. UXXЭГ – отрицательная величина.
Расчет искомого тока. Согласно закону Ома для полной цепи:
IХ = 
.
Подставив в полученные выражения числовые значения получаем:
IХ= 0,566 А.
Баланс мощностей
Поскольку в цепи постоянного тока не происходит накопления энергии, согласно закону её сохранения, сумма мощностей, расходуемых в пассивных двухполюсниках и мощностей теряемых внутри генераторов должна быть равна алгебраической сумме мощностей, отдаваемых всеми генераторами:
. (5)
Соотношение 4.1 и называется балансом мощностей ЭЦ постоянного тока.
Анализируемая схема может содержать источники двух видов: ИИН и ИИТ, поэтому левую часть равенства 4.1 можно представить в виде:
(6)
где In – ток ветви с ИИН (всего ИИН – N), (φa – φb) – разность потенциалов зажимов ИИТ (всего ИИТ – M).
Пример 11
Рассчитать баланс мощностей для схемы рис.1, воспользовавшись результатами расчета токов примера 1. Согласно соотношениям (5) и (6) выражение, описывающее баланс мощностей, имеет вид:
.
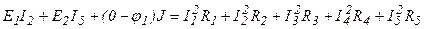В числовом выражении (величину φ1 возьмем из примера 7) получаем примерное, обусловленное конечной разрядностью, равенство 55 ≈ 56.
 | |||
