∆ Матрица 
имеет размеры 
, матрица 
– размеры 
. Если поставить рядом размеры матриц и , получим – центральные числа не совпадают, значит, произведение 
не определено. Если же поменять порядок, получим – центральные числа совпадают, произведение 
существует. Обозначим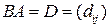 
. На основании замечания 1 матрица 
имеет размеры 
. Приведем подробное вычисление некоторых ее элементов.
Элемент 
расположен в первой строке и первом столбце. На основании замечания 2 для его вычисления первую строку матрицы (первого сомножителя) умножаем на первый столбец матрицы (второго сомножителя): 
.
Элемент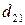 
расположен во второй строке и первом столбце. Для его вычисления вторую строку матрицы умножаем на первый столбец матрицы : 
.
Элемент 
расположен во второй строке и третьем столбце. Для его вычисления вторую строку матрицы умножаем на третий столбец матрицы : 
.
Аналогично вычисляются оставшиеся элементы матрицы-произведения, и в результате мы получаем 
.
Из остальных произведений существуют 
и 
, их также вычислим:
;
.
Конечно, по приобретении опыта матрицы надо перемножать устно, а не расписывать вычисления так подробно. ▲
Пример 10.3. Найти произведения 
и 
, если
.
∆ 
;
▲
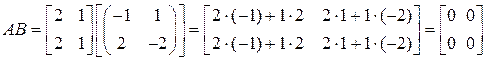Из приведенных примеров видим: в том случае, когда оба произведения и существуют, они могут быть как одинаковыми, так и разными. Они даже могут иметь разные размеры. Поэтому говорят, что произведение матриц, вообще говоря, не коммутативно. Если же произведения и совпадают, то матрицы и называются перестановочными или коммутирующими. Перестановочными могут быть только квадратные матрицы одного и того же порядка. Второй пример также показывает, что произведение матриц не обладает еще одним известным свойством произведения чисел: если произведение равно 0, то один из сомножителей равен 0. В приведенном примере произведение ненулевых матриц является матрицей нулевой. Поэтому в матричных равенствах ни в коем случае нельзя сокращать на матрицу.
Пример 10.4. Найти произведения и , если
.
∆ На основании определения произведения матриц получаем:
.
Так как в полученной матрице аргументы 
и 
равноправны, то, очевидно, = . Кроме того, из результата видим, что при умножении матриц такого вида аргументы и просто складываются. ▲
Пример 10.5. Заданы матрицы
, 
, 
.
Вычислить произведения а) 
, б) 
и 
.
Найти также все матрицы , перестановочные с матрицей 
.
∆ а) 
.
Заметим, что при таком умножении каждый столбец матрицы умножается на диагональный элемент матрицы , имеющий тот же номер. В частности, при умножении диагональных матриц просто перемножаются их соответствующие диагональные элементы.
б) 
;
.
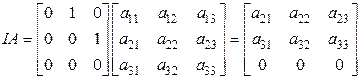При умножении матрицы на справа каждый столбец матрицы передвигается на одну позицию вправо, последний уничтожается, а первый заменяется нулевым столбцом. При умножении матрицы на слева каждая строка матрицы передвигается на одну позицию вверх, первая уничтожается, а последняя заменяется нулевой строкой.
Сравнивая матрицы и , делаем вывод, что они совпадают в том и только в том случае, когда 
, 
, 
. Итак, все матрицы, перестановочные с матрицей , имеют вид
.
В частности, этому условию удовлетворяют все диагональные матрицы. ▲
Пример 10.6. Следом квадратной матрицы называется сумма ее диагональных элементов. След матрицы обозначается 
. Доказать, что для произвольных перестановочных матриц и 
.
∆Так как матрицы и перестановочны, то они квадратные и имеют одинаковый порядок. Пусть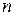 
– общий порядок матриц и , 
, 
, 
; 
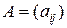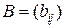. Тогда:
, 
,
.
Сделаем замену индекса во втором слагаемом, т.е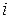 
и 
, а также воспользуемся тем фактом, что в двойном суммировании порядок суммирования можно менять. Получаем:
,
что и требовалось доказать. ▲
