ГЛАВА 10. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
Матрицы и линейные операции над ними
Основные определения. Матрицей размеров 
называется таблица, имеющая 
строк и 
столбцов и состоящая из действительных или комплексных чисел.
Матрицу сокращенно обозначают одной большой буквой латинского алфавита, например 
. Если нужно указать размеры матрицы, то их можно записать в качестве индекса: 
. Элементы матрицы, как правило, обозначаются той же буквой латинского алфавита, что и сама матрица, но малой, и снабжаются двумя нижними индексами, первый из которых обозначает номер строки, а второй – номер столбца. Так, 
обозначает элемент матрицы , расположенный в 
-й строке 
-м столбце. Но запись 
(т. е. 
в круглых скобках) – это сокращенная запись всей матрицы. Вертикальный ряд в матрице называется ее столбцом, а горизонтальный – строкой.
В развернутом виде матрица записывается, согласно определению, как числовая таблица, при этом с обеих сторон она ограничивается либо круглыми скобками, либо квадратными, либо двумя вертикальными чертами, например:
.
Матрица называется нулевой и обозначается 
, если все ее элементы равны нулю. Если 
, то матрица 
называется квадратной, а число называется ее порядком. Элементы 
, 
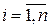квадратной матрицы образуют ее главную диагональ и называются диагональными. Элементы 
образуют побочную диагональ матрицы.
Квадратная матрица, в которой все элементы, расположенные вне главной диагонали, равны нулю, называется диагональной. Следует отметить, что в диагональной матрице некоторые диагональные элементы также могут равняться нулю.
Среди диагональных матриц выделяют матрицу 
, все диагональные элементы которой равны 1, и называют эту матрицу единичной:
.
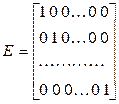Если обозначить элементы единичной матрицы 
, то
.
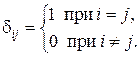Символ 
, снабжённый двумя индексами, верхними или нижними (
), равный 1, когда индексы совпадают, и 0, когда они разные, широко применяется как в математике, так и в физике, и называется символом Кронекера. Таким образом, элементы единичной матрицы совпадают с соответствующими символами Кронекера.
Квадратная матрица 
называется верхней треугольной, если 
при 
, нижней треугольной, если при 
. Неквадратная матрица при 
называется трапециевидной, если при .
Матрицы, у которых совпадают размеры и соответствующие элементы равны, называются равными.
Сложение матриц
Определение 10.1. Суммой двух матриц одинаковых размеров называется матрица тех же размеров, каждый элемент которой равен сумме соответствующих элементов матриц-слагаемых. Другими словами, если 
, 
, то 
.
Свойства сложения матриц.
1. 
(коммутативность).
2. 
(ассоциативность).
3. 
(существование нейтрального элемента).
4. 
(существование противоположного элемента).
Во множестве матриц одинаковых размеров задаётся и операция вычитания как операция, обратная сложению. Поэтому вычитание матриц сводится к вычитанию их соответствующих элементов.
Умножение матрицы на число
Определение 10.2. Произведением матрицы 
на число 
называется матрица 
тех же размеров, что и , все элементы которой получены из соответствующих элементов матрицы умножением на число .
Другими словами, при умножении матрицы на число все ее элементы умножаются на то же число.
