Определение приведенного давления

Залежь не разрабатывается, т.е. нах-ся в термодинамической равновесии.

Р₁=Р₂ е^S – барометрическая формула Лапласа-Бабинэ.

S=0,03415 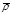ΔН/(z_срТ_пл)

Для оценки величины Р_пл замеры в оставленных скважинах приводят к единой горизонтальной плоскости. Этой плоскостью м.б. либо начальное положение ГВК, либо середина этажа газоносности.

1) НГВК

Р ^прив₁=Р₁ е^S1 : S₁=0,03415 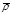h₁/(z_ср1Т_пл)

Р ^прив₂=Р₂ е^{S 2}: S₁=0,03415 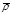h₂/(z_ср2Т_пл)

Р ^прив₁= Р ^прив₂=Р^НГВК_пл

2) середина h

Р^‘прив₁=Р₁е^–S’1

S^‘₁=0,03415 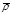h^‘₁/(z ^‘_ср1Т_пл)

Р^‘прив₂=Р₂е^+S2 :

S₁=0,03415 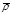h ^‘₂/(z ^‘_ср2Т_пл)

Р^‘прив₁= Р^‘прив₂=Р^{сер h}_пл

В разраб. залежи:

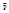=1/Ω∫ Р(Ω)d Ω

 

 

 

3 (30) Применение принципа суперпозиции в расчётах внедрения краевой воды в газовую залежь.

Имеется залежь радиусом R_з, заданы Q_доб^ст(t), W_н, k, k_в – фазовая проницаемость воды в газонасыщ-й области, h, m, m_в, Р_н, Т_пл, z(P,T_пл).

Требуется рассчитать q_в(t), Q_в(t), (t), R(t).

В реальных усл-х дебит воды в залежь меняется со временем. Поэтому решения:

Q_в(t)=2p×k×h×R_c²DP× (fo)/(m_в×c) (1)

Р_н-Р(R_c,t)=m_в×Q_в× (fo)/(2p×k×h) (2)

полученные в теории укрупненной скв-ны исп-ть нельзя.

В этом случае удобно применить принцип суперпозиции к решению (1) или (2).

Q_в(t_n)=

Для линейных ДУ, в том числе и для частных производных возможно применение принципа суперпозиции. Общее понижение Р равно сумме понижений Р, вызванных работой n скв-н с постоянным дебитом q=Dq_вj.

P_н-Р(R_з,t_n)=SDP_j; j=1,n (3)

P_н-Р(R_з,t_n)=P_н-m_в/(2p×k×h)×S[Dq_вj× (fo_n-fo_n-1)]; j=1,n (4) где fo_j=0=0, Dq_вj=0=0.

Расчет ведется по рекурентным соотношениям. Выделим из (4) слагаемое с номером n:

P_н-Р(R_з,t_n)=P_н-m_в/(2pkh)( -

-Dq_в(t_n) (fo_n-fo_n-1)) (5)

q_в(t_j)=q_в(t_j-1)+Dq_в(t_j) (6)

q_в(t_n)=q_в(t_n-1)+Dq_в(t_n) (7)

Q_в(t)=Q_в(t_n-1)+[q_в(t_n-1)+Dq_в(t_n)]×Dt (8)

(9)

Противодавление созд-е столбом воды высотой y(t) равно r_в×g×y(t) на НГВК. Воспользуемся методом последовательной смены стац-х состояний из формулы Дюпюи.

Р(R_з,t)-Р(R,t)=m_в/(2×p×k_в×h)×ln[R_з/R(t)]×[q_в(t_n-1)+Dq_в(t_n)] (10)

С учетом противодавления на НГВК (10)

Р¢(R,t)= 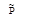+r_в×g×y(t) (11)

P(R_з,t)-[ (t)+r_в×g×y(t)]=m_в/(2×p×k_в×h)×ln[R_з/R(t)]×

×[q_в(t_n-1)+Dq_в(t_n)] (12)

Исключая Р из (12) с учетом (9) и (5) получим:

Р_н-m_в/(2pkh)(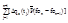 -Dq_в(t_n)×

× (fo_n-fo_n-1))= +

+r_в×g×y(n)+m_в/(2pkh)×ln(R_з/R(t_n))×[q_в(t_n-1)+Dq_вn] (13)

(13) квадратное отн-но Dq_в(t_n)

Dq_в(t_n)=b/(2×a)-(b²/(4×a²)-c/a (14)

гдеа=m_в/(2×p×k×h)(Dt× (fo_n-fo_n-1)+ln[R_з/R(t_n)])

b=Р_нDt-m_в/(2×p×k×h)×Dt×q_в(t_n-1)-ln[R_з/R(t_n)]+

+L×m_в/(2×p×k×h)× (fo_n-fo_n-1)-

-m_в/(2×p×k×h)×Dt +

+L×m_в/(2×p×k×h)×ln[R_з/R(t_n)]

c=Р_н×L-L×m_в/(2×p×k×h) -

-L×m_в/(2×p×k×h)×q_в(t_n-1)×ln[R_з/R(t_n)]-d-r_в×g×y(t_n)L

L= W_н-Q_в(t_n-1)-q_в(t_n-1)×Dt

d=(Р_н W_н/z_н-Р_ат×Т_пл×Q_доб^ст(t_n)/Т_ст)

В (14) входят параметры на момент времени t_n: R(t_n), y(t_n), z(t_n). Поэтому решение производят методом последовательных итераций. В 1-м приближении:

R⁽¹⁾(t_n)=R(t_n-1); y⁽¹⁾(t_n)=y(t_n-1); z⁽¹⁾(t_n)=z(t_n-1)Þq_в⁽¹⁾(t_n)Þ

ÞQ_в⁽¹⁾(t_n) (по 8)Þ 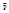⁽¹⁾(t_n)Þz⁽²⁾(t_n)Þ

ÞQ_в(t)=p×[R_з²-R²(t)]mh(a-a_ост)Þ

ÞR(t)=[R_з²-Q_в⁽¹⁾(t_n)/(p×m×h×(a-a_ост))]^0,5Þ

Þy⁽²⁾(t_n)Þf[Q_в⁽¹⁾(t_n)]Þ…

Итерации ведутся до сходимости Р ½Р⁽²⁾(t_n)-Р⁽¹⁾(t_n)½£e

Величина подъема y(t) зав-т от формы залежи.

y=max=H_{этаж газонос-и}

Итерации ведутся до сходимости Р. Рез-ты расчетов сравнивают по давлениям:½Р⁽²⁾(t_n)-Р⁽¹⁾(t_n)½£e

 

4 (29) Теория укрупненной скв-ны Ван Эвердингена и Херста для расчёта внедрения воды в газовую залеж (случай постоянного дебита и постоянной депрессии).

При иссл-и проявления водонапорного режима ГЗ часто аппроксимируется укрупненной скв-ной. На теории укрупненной скв-ны основаны методики прогнозирования показателей разр-и при водонапорном режиме.

Укрупненная скв-на радиусом R_з дренирует однородный по коллекторским свойствам водоносный пласт с постоянным во времени дебитом воды q_в. Согласно решению Ван Эвердингена и Херста, изменение во времени давления P(R_3,t) на стенке укрупненной скв-ны определяется:

P(R_з,t)=P_н-q_в×m_в×Р(fo)/(2×p×k×h) (1)

где fo=хt/R²_З; h, k, n — толщина и коэффициенты проницаемости и пьезопроизводности водоносного пласта соответственно; m_b-коэффициент динамической вязкости воды; P(fo) — табулированная функция параметра Фурье fo.

Пусть укрупненная скв-на эксплуатируется с постоянным во времени противодавлением DP=Р_н—Р(R_з,t) на водоносный пласт. Для вычисления суммарного кол-ва воды Q_B, к-е поступит в залежь к моменту t:

Q_в(t)=2×p×k×h×R_з²×DР×Q(fo)/(m_в×х) (2)

где Q(fo) — табулированная функция пар-ра Фурье fo. Таблицы функций P(fo) и Q(fо) составлены для случаев ¥ по протяженности, конечного замкнутого и открытого водоносного пласта. В качестве ¥ водоносный пласт может рассм-ся при усл-и R_K/R₃>20, где R_к — радиус внешней границы пласта. Решения (1) и (2), полученные для случаев соответственно q_в=const и Dр=const, используются, благодаря принципу суперпозиции, для переменных во времени граничных усл-й на забое укрупненной скв-ны Hа начальных этапах проектирования разр-и ГМ и ГКМ информация о необходимых для соответствующих расчетов исходных данных еще недостаточна и невысока ее достоверность. При оценочных расчетах поступления в залежь подошвенной воды допустимо пренебрегать потерями Р в обводненной зоне пласта. Водоносный пласт принимается однородным по коллекторским свойствам и постоянным по толщине, т.е. заменяется эквивалентным пластом со средними параметрами. Примем следующую схематизацию. UP представляется укрупненной скв-ной радиусом R_З. Радиус укрупненной скв-ны определяется из равенства pR_З=S (здесь S — площадь газоносности). Если возмущение, вызванное разр-й ГЗ, за рассматр-й период не достигает внешней границы, то водоносный пласт принимается ¥ по протяженности. В противном случае водоносный пласт представляется круговым с радиусом R_к.

Известны запасы г, начальные Р_пл и Т_пл, параметры водоносного пласта, наличие или отсутствие области питания и др.

Необходимо определить показатели разр-и ГЗ при ВНР, при к-х обеспечивается получение заданного отбора гQ=Q(t).

Расчеты основаны на методе последовательных приближений и использовании решения для неустановившегося притока воды к укрупненной скв-не.

Продвижение в залежь подошвенной воды определяется изменением во времени среднего Р_пл, т.е. оправдано принятие допущения о равенстве среднего Р в залежи и Р_з на стенке укрупненной скв-ны Р(R₃,t)@Р(f). Пусть среднее Р в залежи изменяется как на рис. 1.

Рис. 1. Аппроксимация зависимости изменения во времени среднего Р_пл ступенчатой зависимостью. Требуется найти суммарное количество воды, к-е поступит в залежь к нек-у моменту t. Тогда интервал времени [0,t] разбивается на п одинаковых интервалов с шагом Dt. Зависимость Р=Р(t) приведенная на рис. 1, аппроксимируется ступенчатой зависимостью. Согласно решению (2) и принципу суперпозиции, суммарное количество воды, к-ое поступит в залежь к рассматриваемому моменту t, определится по формуле(5): Q_в(t)=2×p×k×h×R_з²/m_в(DР₀Q(fo)+DР₁Q(fo-fo₁)+DР₂Q(fo-fo₂)+…+DР_nQ(fo-fo_n)), где приращения давлений DР₀, DР₁, DР₂ и т.д. определяют приток воды в течение t, (t—t₁), (t—t₂) и т.д. соответственно (см. рис. 1):

fo=хt/R²_З; fo-fo₁=х(t-t₁)/R²_З; fo-fo₂=х(t-t₂)/R²_З;

Определив по графику на рис. 1 приращения среднего пластового давления Dр₀, Dр₁, Dр₂ и т.д., вычислив аргументы функции Q и соответствующие значения самой функции, по формуле (5) находим Q_в(t). Проводя аналогичные расчеты для других моментов, определяем зависимость изменения во времени суммарного количества воды, поступающей в газовую залежь: О_в = Q_в(t) (6)

Указанный порядок расчетов возможен при проведении анализа разр-и газовой залежи при водонапорном режиме. В этом случае известны средние пластовые давления на прошедшие даты, т.е. располагаем графической

4. При иссл-и проявления ВНР ГЗ часто аппроксимируется укрупненной скв-ной. На теории укрупненной скв-ны основаны методики прогнозирования показателей разр-и при водонапорном режиме.

В уравнении материального баланса для ВНР при изв-й динамике отбора г неизвестными явл-ся Р_пл.

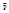(t)/z(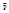)=1/[a×W_н-Q_в(t)]×[P_н/z_н×aW_н-Р_ат×Т_пл×Q_доб^ст(t)/Т_ст] (1)

где Q_в(t) – объем добытой скв-й воды.

Þ необходимо располагать динамикой внедрения пластовой воды, чтобы опр-ть динамику падения Р. В 1949 г. Ван-Эвердинген и Херст разработали теорию укрупненной скв-ны. Они решили уравнение пьезопроводности для радиального пласта о притоке воды к скв-е конечного радиуса.

¶²Р/¶r²+1/r׶P/¶r=1/c׶P/¶t (2)

где c - коэф-нт пьезопроводности;

c=k×K/(m×m_в)

где К – объемный модуль упругости

Размером укрупненной скв-ы по сравнению с пластом пренебречь нельзя.

Р(r,t=0)=P_н=const – начальные условия(3). Граничные условия

Внешние границы:а) P(R_к,t)=P_н – открытая система(4);б) (¶Р/¶r)½_r=Rк=0 – замкнутый водоносный пласт(5).

Внутренние границы (контур): а) P(R_к,t)- P(R_з,t)= DP= const (6);

б) (r¶Р/¶r)½_r=Rз= const (7)

q_в=2×p×R_зk×h(¶P/¶r)½_r=Rз/m_в =const

(r¶Р/¶r)½_r=Rз=m_в q_в/2×p×k×h= const^*

Интегрирования уравнения 2 при 3,5,6, дает решение Q_в(t)=2×p×k×h×R_з²×DP× (fo) /(m_в×c) (8)

где fo – пар-р Фурье (время Фурье, безразмерное время); fo=c×t/R_з²; (fo) – безразмерная функция пар-ра Фурье при R_к®¥:

где I₀, Y₀ – функция Бесселя 1-го и 2-го рода, 0-го порядка.

Р_н-Р(R_з,t)=m_в×Q_в× (fo) /(2×p×k×h) (9)

где (fo) - безразмерная функция пар-ра Фурье при R_к®¥:

(fo)=

где I₁, Y₁ – функция Бесселя 1-го и 2-го рода, 1-го порядка.

F=p×R_з²®R_з=(F/p)^0,5