Активная ветвь, названная так из-за наличия источника ЭДС, изображена на рисунке 2.2
Между выходными зажимами ветви возникает напряжение Uab. Индексация показывает направление ко второму индексу. Напряжение – это разность потенциалов между двумя точками:
Uab = Va − Vb.
Определим потенциал точки a, исходя из потенциала Vb. Рассчитаем изменение потенциала промежуточной точки с по сравнению с Vb.
Между точками b и c расположен источник ЭДС, поэтому потенциал точки с отличается от потенциала точки b на величину Е. Стрелка источника показывает направление увеличения потенциала. Следовательно, потенциал точки с ниже потенциала точки b.
Между точками с и а находится резистор сопротивлением R. Потенциал Va отличается от потенциала Vc величиной напряжения на резисторе RI. Ток направлен от большего потенциала к меньшему, поэтому потенциал Va выше потенциала Vc.
Va = Vb − E + RI,
Va − Vb = − E + RI.
Но Va − Vb = Uab, т. е. Uab = − E + R I.
Можно определить напряжение между двумя любыми точками, рассчитав изменение потенциалов между ними. При этом нужно вести расчет в сторону увеличения потенциала, т. е. от второго индекса напряжения к первому.
Решим уравнение относительно тока:
, где 
– проводимость ветви.
Это выражение называют законом Ома для активной ветви.
Последнее выражение можно составить исходя из следующих рассуждений. Для появления тока в ветви есть два условия:
1) Наличие разности потенциалов между концами ветви и действие источника ЭДС.
2) Если направления ЭДС и напряжения Uаb совпадают с направлением тока, они
способствуют его появлению и должны быть записаны в уравнение со знаком +. В противном случае со знаком минус. Рассуждая, таким образом, получим для тока ветви прежнее выражение.
8.Энергетический баланс в электрических цепях.
При протекании токов по сопротивлениям в последних выделяется теплота. На основании закона сохранения энергии количество теплоты, выделяющееся в единицу времени в сопротивлениях схемы, должно равняться энергии, доставляемой за то же время источником питания. Если направление тока I, протекающего через источник ЭДС E, совпадает с направлением ЭДС, то источник ЭДС доставляет в цепь энергию в единицу времени (мощность), равную EI, и произведение EI входит в уравнение энергетического баланса с положительным знаком.
Если же направление тока I встречно направлению ЭДС Е, то источник ЭДС не поставляет энергию, а потребляет ее (например, заряжается аккумулятор), и произведение EI войдет в уравнение энергетического баланса с отрицательным знаком.
Уравнение энергетического баланса при питании только от источников ЭДС имеет вид
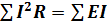
Когда схема питается не только от источников ЭДС, но и от источников тока, т. е. к отдельным узлам схемы подтекают и от них утекают токи источников тока, при составлении уравнения энерге-тического баланса необходимо учесть и энергию, доставляемую источниками тока. Допустим, что к узлу а схемы подтекает ток I от источника тока, а от узла b этот ток утекает. Доставляемая источником тока мощность равна UabJ. Напряжение Uab и токи в ветвях схемы должны быть подсчитаны с учетом тока, подтекающего от источника тока. Последнее проще всего сделать по методу узловых потенциалов (см. § 2.22). Общий вид уравнения энергетического баланса:
Для практических расчетов электрических цепей разработаны методы, более экономичные в смысле затраты времени и труда, чем метод расчета цепей по законам Кирхгофа.
Основные понятия и определения.
Электрические цепи, в которых величины и направления э. д. с., напряжения и тока периодически изменяются во времени по синусоидальному закону, называются цепями синусоидального тока (переменного тока). Синусоидальная э. д. с. В линейных цепях, где содержатся активные сопротивления, индуктивности и ёмкости, возбуждает ток, изменяющийся по закону синуса. Возникающие при этом э. д. с. Самоиндукции в катушках и напряжения на конденсаторах, как это вытекает из выражения:
, 
Также изменяются по закону синуса, так как производная синусоидальной функции есть функция синусоидальная. Напряжение на сопротивлении будет также изменяться по синусоидальному закону, так как:
За один оборот рамки происходит полный цикл изменения э. д. с.. Если при t=0 э. д. с. e не равна нулю, то выражение э. д. с. записывается в виде:
Где e – мгновенное значение э. д. с. в любой момент времени;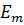 
– максимальное значение э. д. с. или её амплитуда; 
– аргумент синуса или фаза, характеризующая значение э. д. с. в данный момент времени; 
– начальная фаза, определяющая значение э. д. с. при t=0.
Время, в течение которого совершается один цикл периодического процесса, называется периодом Т, а число периодов в секунду – частотой f:
f=1/T
Эквивалентным, или действующим называется такой неизменный во времени ток, который выделяет в сопротивлении r за период то же количество энергии, что и действительный, изменяющийся по синусоидальному закону ток. Действующее значение тока меньше амплитудного в 
раз.
