Если два параллельных проводника с током находятся в вакууме (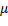
= 1), то сила взаимодействия на единицу длины проводника, согласно (111.5), равна (112.1)
Для нахождения числового значения 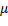0 воспользуемся определением ампера, согласно которому 
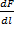= 2 • 10-7Н/м при I1 = I2 = 1 А и R — 1 м. Подставив это значение в (112.1), получим 
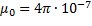Н/А2 = 4 
Гн/м.
Единица индуктивности — генри (Гн).
Закон Ампера позволяет определить единицу магнитной индукции В. Предположим, что элемент проводника dl с током I перпендикулярен направлению магнитного поля. Тогда закон Ампера запишется в виде dF = IBdl, откуда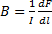 
Единица магнитной индукции — тесла (Тл): 1 Тл — магнитная индукция такого однородного магнитного поля, которое действует с силой 1 Н на каждый метр длины прямолинейного проводника, расположенного перпендикулярно направлению поля, если по этому проводнику течет ток 1 А: 1 Тл=1Н/(А·м)
Так как 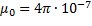Н/А2, а в случае вакуума (
), согласно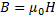 
, то для данного случая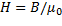 
Единица напряженности магнитного поля — ампер на метр (А/м): 1 А/м —напряженность такого поля, магнитная индукция которого в вакууме равна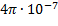 
Тл.
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера.
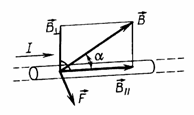Сила действия однородного магнитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником: F=BIℓsin a — закон Ампера.
Направление силы Ампера (правило левой руки) Если левую руку расположить так, чтобы перпендикулярная составляющая вектора В входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90° большой палец покажет направление силы, действующей на проводник с током.
Сила, действующая на заряженную движущуюся частицу в магнитном поле, называется силой Лоренца:
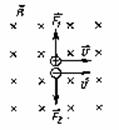
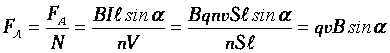
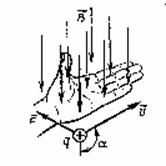Направление силы Лоренца (правило левой руки) Направление F определяется по правилу левой руки: вектор F перпендикулярен векторам В и v.
Правило левой руки сформулировано для положительной частицы. Сила, действующая на отрицательный заряд будет направлена в противоположную сторону по сравнению с положительным.
33. Магнитные силовые линии и магнитный поток. Работа магнитных сил. Теорема Гаусса для магнитного поля.
Линии магнитной индукции - линии, касательные к которым направлены также как и вектор магнитной индукции в данной точке поля. Магнитные поля, так же как и электрические, можно изображать графически при помощи линий магнитной индукции. Через каждую точку магнитного поля можно провести линию индукции. Так как индукция поля в любой точке имеет определённое направление, то и направление линии индукции в каждой точке данного поля может быть только единственным, а значит, линии магнитного поля, так же как и электрического поля, линии индукции магнитного поля прочерчивают с такой густотой, чтобы число линий, пересекающих единицу поверхности, перпендикулярной к ним, было равно (или пропорционально) индукции магнитного поля в данном месте. Поэтому, изображая линии индукции, можно наглядно представить, как меняется в пространстве индукция, а следовательно, и напряжённость магнитного поля по модулю и направлению.
Силовые линии электрических и магнитных полей - линии, касательные к которым в каждой точке поля совпадают с направлением напряженности электрического или соответствующего магнитного поля; качественно характеризуют распределение электромагнитного поля в пространстве. Силовые линии - только наглядный способ изображения силовых полей.
Направление линии магнитной индукции определяется по правилу правой руки (правило буравчика).
Линии магнитной индукции прямого проводника с током представляют концентрические окружности, лежащие в плоскости, перпендикулярной току.
Линии магнитной индукции всегда замкнуты и охватывают проводники с токами. Это отличает их от линий напряженности (силовых линий) электрического поля. Замкнутость линий магнитной индукции означает то, что в природе не существует магнитных зарядов.
В однородном магнитном поле, модуль вектора индукции которого равен В, помещен плоский замкнутый контур площадью S. Нормаль n к плоскости контура составляет угол α с направлением вектора магнитной индукции В.
Магнитным потоком через поверхность называется величина Ф, определяемая соотношением:
Φ = B · S · cos α
Единица измерения магнитного потока в системе СИ - 1 Вебер (1 Вб).
1 Вб = 1 Тл · 1 м2
Магнитный поток через контур максимален, если плоскость контура перпендикулярна магнитному полю. Значит угол a равен 00.
Тогда магнитный поток рассчитывается по формуле:
Φmax = B · S
Магнитный поток через контур равен нулю, если контур располагается параллельно магнитному полю.
Значит угол α равен 900.
Теорема Гаусса для поля В: поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю: (120.3)
Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.
Итак, для потоков векторов В и Е сквозь замкнутую поверхность в вихревом и потенциальном полях получаются различные выражения.
В качестве примера рассчитаем поток вектора В сквозь соленоид. Магнитная индукция однородного поля внутри соленоида с сердечником с магнитной проницаемостью 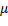, согласно (119.2), равна
Магнитный поток сквозь один виток соленоида площадью S равен а полный магнитный поток, сцепленный со всеми витками соленоида и называемый потокосцеплением,
