1. Для определения углового коэффициента касательной находим
производную заданной функции:
.
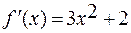Значение производной в точке с абсциссой x о= 1 даёт искомый
угловой коэффициент
.
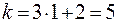Значение функции 
в точке x о= 1:
.
Воспользовавшись уравнением
,
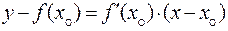получим уравнение касательной:
или 
,
а уравнение нормали получим, используя уравнение
.
Таким образом, уравнение нормали имеет вид:
или 
.
Ответ: - уравнение касательной,
- уравнение нормали.
2. Воспользуемся приближённой формулой
.
Учитывая, что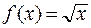 
, x о= 25, 
, получим
,
т.е.
.
Ответ: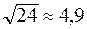 
.
3. Найдём коэффициент эластичности данной функции 
по
формуле
.
Имеем
.
Так как 
то данная функция является эластичной
в точке x о= 1.
Ответ: функция 
является эластичной в
точке x о= 1.
4 а). Поскольку 
и 
,
то в данном случае имеем неопределённость вида 
.
Воспользуемся правилом Лопиталя:
.
4 б). Здесь также имеет место неопределённость вида , так как
и 
.
Применяем правило Лопиталя:
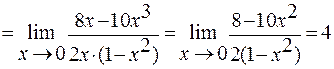
Ответ: 4 а) 
; 4 б) 4.
5. Данная функция определена на всей числовой прямой, т.е. D(f) = R, а её производная равна
Производная обращается в нуль в трёх точках х = -1, х = 
, х =1.
Эти точки разбивают область определения функции на четыре промежутка (-¥,-1), (-1, ), (,1) и (1, +¥), в каждом из которых производная f' (x)сохраняет знак.
Подставим в выражение для f' (x) значения х = -2, х = 0, х =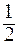 
, х = 2 из указанных промежутков, тогда:
на (-¥,-1) имеем f' (-2)< 0;
на (-1, ) имеем f' (0)> 0;
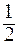на (, 1) имеем f' ()< 0;
на (1, +¥) имеем f' (2) >0.
Следовательно, в промежутках (-¥,-1) и(,1) функция убывает, а в промежутках
(-1, ) и (1, +¥) – возрастает.
6. Функция определена и дифференцируема на всей числовой прямой, причём
Производная обращается в нуль в точках: х = 
, х = 
и не существует в точке х = 0.
Эти три точки делят область определения на четыре промежутка
(-¥, ), (, 0), (0, ) и (, +¥).
Определим знак производной в каждом из них
на (-¥, ) имеем f' (-1) > 0;
на (, 0) имеем f' (
)< 0;
на (0, ) имеем f' (
)< 0;
на (, +¥) имеем f' (1) >0.
Таким образом, в промежутках (-¥, )и (, +¥) функция возрастает, а в промежутке (, ) – убывает.
7. Область определения функции D(f) = R. Дифференцируя данную функцию, находим
Производная обращается в нуль при х = 
, х = 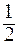и х =1. Эти точки разбивают числовую ось на четыре промежутка(-¥, ), (, 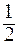), (,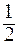1) и (1,+¥), внутри которых производная сохраняет определённый знак. Найдём знак производной в каждом из указанных промежутков:
на (-¥, ) имеем f' (-1) < 0;
на (, 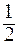) имеем f' (0) > 0;
на (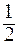,1) имеем f' (
)< 0;
на (1, +¥) имеем f' (2) >0.
Отсюда следует, что точки х = , х = 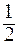и х = 1 являются экстремальными, так как при переходе через каждую из них производная меняет свой знак. При этом в точках х = и х = 1 происходит смена знаков с минуса на плюс, т.е. это - точки минимума; при переходе через точку х = 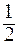знак производной меняется с плюса на минус, значит, это - точка максимума.
Найдем экстремумы функции, вычислив её значения в экстремальных точках:
fmin = f () = 
, fmax = f () =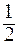 
, fmin = f (1) = 1.
8. Представим функцию в виде: 
.
Область определения функции D (f) – вся числовая прямая,
за исключением точек х = -2 и х = 6, т.е.
.
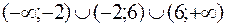Функция непериодическая; исследуем её на четность,
нечетность
,
.
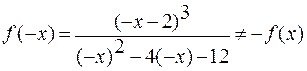Следовательно, данная функция не является ни чётной,
ни нечётной.
Найдём точки пересечения графика с осями
координат:
с осью О у график пересекается при х = 0, при этом
у = f (0) = 
,
т.е. М (0; ) - точка пересечения с осью О у;
с осью О х график пересекается в точках, в которых
f (х) = 0, т.е.
,
откуда х = 2.
Таким образом, М (2; 0) - точка пересечения с осью О х.
Находим интервалы знакопостоянства функции:
f (х) > 0 
,
т.е. при 
.
Аналогично f (х) < 0 при 
.
Так как
,
,
,
,
то х = -2 и х = 6 являются точками разрыва второго рода,
а прямые х = -2 и х = 6 - вертикальными асимптотами.
Поскольку 
, а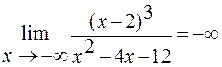 
,
то горизонтальных асимптот график функции не имеет.
Наклонная асимптота задаётся уравнением 
, где
,
,
т.е. прямая 
- наклонная асимптота при 
и при 
.
Найдём интервалы монотонности и экстремумы функции, исследуя первую производную:
.
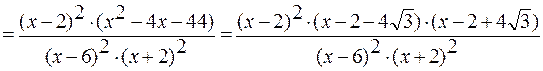Воспользуемся методом интервалов для исследования знака производной (см. рис.1):
Рис.1
При 
и при 
производная 
, следовательно, функция возрастает.
Пр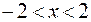и 
, 
, 
и 
производная 
, следовательно, функция убывает.
При переходе через точку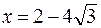 
, производная меняет знак с «+» на «-», значит это точка локального максимума.
При переходе через точку 
, производная меняет знак с «-» на «+», значит это точка локального минимума.
При переходе через точку х = 2, производная знака не меняет, значит в этой точке функция экстремумов не имеет.
Чтобы определить интервалы выпуклости и точки перегиба, вычислим вторую производную:
.
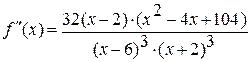Применим метод интервалов для исследования знака второй производной (см. рис. 2):
Рис. 2
При 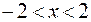и 
, следовательно, функция выпукла вниз,
При 
и 
, следовательно, функция выпукла вверх.
Учитывая всю полученную информацию о функции, строим график:
Рис. 3
