Проверочная работа №2– 0
(с решением)
1. Пользуясь определением предела последовательности, доказать, что  = а, если:
= а, если:
а) хn =  , а =
, а =  ; б) хn =
; б) хn = 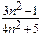 , а =
, а =  . Указать номер
. Указать номер  .
.
2. Найти предел числовой последовательности. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
Решение проверочной работы №2– 0.
1.а) Найдём | хn –  | = |
| = | 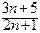 –
–  | = |
| = |  | = |
| = |  | =
| =  . Определим, при каком значении n выполняется неравенство
. Определим, при каком значении n выполняется неравенство  < e. Так как 2(2 n + 1) >
< e. Так как 2(2 n + 1) >  , то 4 n + 2 >
, то 4 n + 2 >  или 4 n >
или 4 n >  – 2, откуда n >
– 2, откуда n >  . Поэтому за
. Поэтому за  возьмём целую часть числа
возьмём целую часть числа  .
.
Таким образом, для любого e > 0 найдено такое число  = [
= [  ], что при всех n >
], что при всех n > 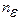 выполняется неравенство | хn –
выполняется неравенство | хn – 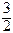 | < e, откуда по определению следует, что
| < e, откуда по определению следует, что
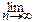
 =
=  .
.
2.б) Задав произвольное положительное e, решим неравенство | хn –  | < e, т.е.
| < e, т.е.
|  –
–  | = |
| = |  | =
| =  < e,
< e,
откуда находим 4(4 n 2 + 5) >  , или n >
, или n >  .
.
Полагая  = [
= [  ], получаем, что при n >
], получаем, что при n >  выполняется неравенство | хn –
выполняется неравенство | хn –  | < e, т.е. число
| < e, т.е. число  по определению является пределом данной последовательности.
по определению является пределом данной последовательности.
Ответ. 1.а) 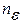 = [
= [  ]; 2.б)
]; 2.б)  = [
= [  ].
].
2. а) Преобразуем выражение  , поделив почленно числитель и знаменатель на n 2:
, поделив почленно числитель и знаменатель на n 2:  . Так как
. Так как  =
=  и
и  =
=  , то
, то
 .
.
б) Разделив числитель и знаменатель на n 2, применяя теорему о пределе частного и теорему о пределе суммы (разности), получим
 =
=  =
= 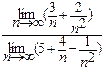 =
=  = 0.
= 0.
в) Разделим числитель и знаменатель на n, внесем в знаменателе 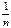 под знак квадратного корня и преобразуем подкоренное выражение:
под знак квадратного корня и преобразуем подкоренное выражение:
 .
.
Перейдя к пределу, получим  =
=
 .
.
г)  =
=  =
=
=  =
= 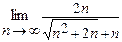 =
=  =1.
=1.
д) Упростим выражение  .
.
Так как
n! = 1· 2 ·3 ·…· n,
(n + 1)! = 1· 2· 3· …· (n + 1),
очевидно, что
(n + 1)! = n! · (n + 1)
и  =
=  =
=  =
=  .
.
Следовательно,  =
=  .
.
Ответ. 2. а) 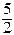 ; 2. б) 0; 2. в)
; 2. б) 0; 2. в)  ; 2. г) 1; 2. д) 0.
; 2. г) 1; 2. д) 0.
Проверочная работа № 3 – 0
(с решением)
1. Используя (e - d) определение предела функции в точке, доказать, что
а) 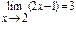 ; б)
; б)  ; в)
; в) 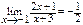 . Указать d (e).
. Указать d (e).
2. Найти предел функции: а) 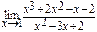 ; б)
; б)  ; в)
; в) 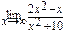 ;
;
г)  ; д)
; д)  ; е)
; е)  ;
;
ж)  ; з)
; з) 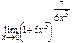 .
.
3. Найти предел функции, заменяя бесконечно малые эквивалентными:
а)  ; б)
; б) 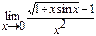 .
.
Решение проверочной работы № 3– 0.
1.а) f (x) = 2 x – 1, b = 3. Нам надо доказать, что для всякого сколь угодно малого положительного числа e существует такое число d, зависящее от e, d > 0, что из неравенства 0 < | x – 2 | < d следует неравенство | f (x) – 3 | < e.
Зададим e > 0 и составим выражение
| f (x) – 3 | = | (2 x – 1) – 3 | = 2 | x – 2 |.
Если взять d £  , то для всех значений х, удовлетворяющих неравенству 0 < | x – 2 | < d,
, то для всех значений х, удовлетворяющих неравенству 0 < | x – 2 | < d,
| f (x) – 3 | = 2 | x – 2 |< 2 d £ 2 ·  = e. Следовательно, по определению
= e. Следовательно, по определению  .
.
1.б) Пусть e - любое положительное число. Требуется доказать, что можно подобрать такое число d, зависящее от e, d > 0, что для всех х, удовлетворяющих неравенству 0 < | x – 2 | < d, будет выполняться неравенство
| x 2 – 4 | < e.
Если | x –2|< d, то | x +2|=| x –2+4| £ | x – 2 | + 4 < d + 4 и | x 2 – 4 | = | x – 2 | | x + 2 |< d (d + 4).
Для выполнения неравенства | x 2 – 4 | < e достаточно потребовать, чтобы d (d + 4) = e или d 2 + 4 d – e =0, откуда
d = – 2 + 
(второй корень квадратного уравнения не удовлетворяет условию, так как d должно быть положительным).
Таким образом, для любого e > 0 найдено такое d > 0, что из неравенства 0 < | x – 2 | < d следует неравенство
| x 2 – 4 | < e, т.е. по определению 
1.в) Пусть e - произвольное положительное число. Требуется доказать, что существует такое число d > 0, что при всех значениях х, удовлетворяющих неравенству 0 < | x + 1 | < d, будет выполняться неравенство
 или
или  .
.
Не теряя общности можно считать, что d < 1.
Поэтому при | x + 1 | < 1 имеем
| x + 3 | = | x + 1 + 2 | > 2 – | x + 1| > 2 – 1 = 1. Тогда 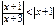 .
.
Чтобы выполнялось неравенство  достаточно, чтобы
достаточно, чтобы  .
.
Таким образом, в качестве d можно взять меньшее из чисел 1 и  .
.
Итак, для любого e > 0 найдено такое d > 0, что из неравенства
0 < | x + 1 | < d следует неравенство  .
.
Таким образом, доказано, что  .
.
Ответ. 1 а) d £  ; 1 б) d = – 2 +
; 1 б) d = – 2 +  или d = min {1,
или d = min {1,  }; 1в) d = min {1,
}; 1в) d = min {1,  }.
}.
2. а) Так как 
 , то имеем неопределённость вида
, то имеем неопределённость вида  . Чтобы раскрыть эту неопределённость, разложим числитель и знаменатель дроби на множители:
. Чтобы раскрыть эту неопределённость, разложим числитель и знаменатель дроби на множители:
х 3 + 2 х 2 – х – 2 =  (х – 1) (х 2 + 3 х + 2),
(х – 1) (х 2 + 3 х + 2),
х 2– 3 х + 2 = (х – 1) (х – 2).

2. б) Имеем неопределённость вида  . Чтобы раскрыть эту неопределённость, умножим числитель и знаменатель дроби на выражение
. Чтобы раскрыть эту неопределённость, умножим числитель и знаменатель дроби на выражение  (сопряжённое числителю).
(сопряжённое числителю).
 =
= 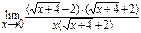 =
=  =
=  =
=  .
.
2в) Имеем неопределённость вида  . Делим числитель и знаменатель почленно на х 2. Тогда
. Делим числитель и знаменатель почленно на х 2. Тогда 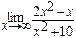 =
= 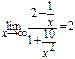 , так как
, так как  и
и  .
.
2. г) Имеем неопределённость вида ¥ – ¥. Умножим и разделим выражение, стоящее под знаком предела на 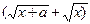 :
:  =
=  =
= 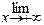
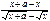 =
=  .
.
2. д) Имеем неопределённость вида ¥ – ¥. Приведем дроби, стоящие под знаком предела, к общему знаменателю, получим новую дробь, числитель и знаменатель которой стремятся к нулю при х ® – 2.

= 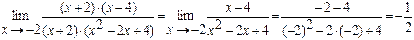
2. е) Имеем неопределённость вида 0· ¥. Запишем функцию, стоящую под знаком предела, в другом виде и перейдём к пределу:
 =
=  =
=  =
=  =
=  ·1·1=
·1·1= 
2. ж) Воспользуемся формулой двойного угла для функции  , получим
, получим
 .
.
В последнем действии умножили числитель и знаменатель на 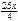 .
.
Воспользовавшись первым замечательным пределом и следствием из него, имеем
 и
и  ,
,
продолжим решение исходной задачи:
 .
.
з) Воспользовавшись вторым замечательным пределом 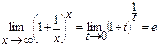 ,
,
получим 


Ответ. 2. а)  ; 2. б)
; 2. б)  ; 2. в) 2; 2. г) 0; 2. д)
; 2. в) 2; 2. г) 0; 2. д) 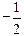 ; 2.е)
; 2.е) 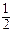 ; 2. ж)
; 2. ж)  ; 2. з)
; 2. з) 
3. а) Так как  при
при 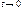 . Это означает, что
. Это означает, что  и одну функцию в пределе можно заменить другой, эквивалентной.
и одну функцию в пределе можно заменить другой, эквивалентной.
Поскольку  при
при 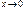 и
и  при
при  , то
, то

 .
.
3. б) Так как  при
при 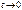 ,
,  при
при  ,
,  при
при  , то
, то
 при
при  .
.
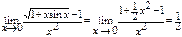 .
.
. Ответ. 3. а) 1; 3. б) 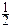 .
.






