1. Пусть D х - приращение аргумента в точке x оÎ R.
Найдем соответствующее приращение функции:
Применяя теоремы о пределе суммы и пределе произведения функций, получим: 
. Значит, по определению функция непрерывна в каждой точке x оÎ R.
2. Рассмотрим односторонние пределы функции в точках, в которых меняется аналитическое задание функции числитель и знаменатель обращаются в ноль): x = -2 и x = 2.
При x ® -2-0 предел рассматривается слева от точки x = -2, имеем:
При x ® -2+0 предел рассматривается справа от точки x = -2, имеем:
.
Так как односторонние пределы конечны, но не равны 
, 
,
то x = -2 является точкой разрыва I рода. Скачок функции в этой точке разрыва равен 2.
Рассмотрим односторонние пределы при x ®2 -0 и x ®2 +0:
,
.
Односторонние пределы конечны и равны, значит существует предел функции в точке x = 2, но функция в этой точке не определена. x = 2 - точка устранимого разрыва.
3. Функция f (x) = 
не определена в точке x о = 1, нарушено условие существования f (1), значит, функция не является непрерывной в этой точке.
Найдём односторонние пределы функции в этой точке:
, 
.
Они конечны, но не равны. Значит, нарушено и второе условие существования предела функции в этой точке. Итак, точка x о = 1 - точка разрыва первого рода.
4. Представим данную функцию в виде: 
.
Рассмотрим односторонние пределы функции в особых точках (в которых числитель и знаменатель обращаются в ноль): x = 1, x = 0, x = -4.
При x ® 1-0 предел рассматривается слева от точки x = 1, значит x < 1 и | x -1| = - (x -1). Имеем: 
.
При x ® 1+0 предел рассматривается справа от точки x = 1, значит x > 1 и | x -1| = (x -1). Имеем: 
.
Так как односторонние пределы конечны, но не равны
, 
,
то x = 1 является точкой разрыва I рода.
Рассмотрим односторонние пределы при x ® -0 и x ® +0:
.
Предел при x ® +0 можно и не рассматривать, поскольку x = 0 уже является точкой разрыва II рода.
Наконец, при x ® -4-0 предел рассматривается слева от точки x = -4 и (x + 4) < 0. Имеем: 
,
значит x = -4 является точкой разрыва II рода и второй односторонний предел можно не рассматривать.
Ответ. x = 1 – точка разрыва I рода, x = 0 и x = -4 - точки разрыва II рода.
5. Пусть D х - приращение аргумента в точке x. Найдем соответствующее приращение функции:
.
Отсюда находим предел отношения 
в точке x при 
:
. Таким образом, по определению 
.
6. а) Требуется найти производную сложной функции, которую можно представить в виде 
, где 
. Поэтому 
. Имеем 
.
6. б) Представим данную функцию в виде: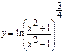 
. Тогда используя свойства логарифмов, имеем:
.
6. в) Так как область определения функции 
,то 
. 
при x < 0.
6. г) 
.
7. Дифференцируя обе части уравнения и учитывая, что у – есть функция от х (поэтому 
и 
), получим: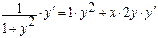 
,
Отсюда находим 
: 
или 
.
8. Производная функции 
находится по формуле 
, откуда 
.
9. Находим первую производную: 
. Отсюда находим вторую производную: 
, а затем искомую третью 
.
10. Запишем формулу Лейбница для n = 3: 
Полагая 
, 
, найдём: 
, 
, 
.
Используя результат предыдущей задачи 
, 
, 
.
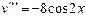Подставляя в формулу Лейбница, получим: 
.
Проверочная работа № 5–0
(с решением)
1. Написать уравнение касательной и нормали к кривой
в точке с абсциссой x о= 1.
2. Вычислить приближенно 
.
3. Проверить, является ли функция 
эластичной в точке x о= 1.
4. Найти пределы, используя правило Лопиталя:
а) 
; б) 
.
5.Найти промежутки монотонности функции:
.
6.Найти промежутки монотонности функции:
.
7. Найти экстремумы функции:
.
8. Исследовать методами дифференциального
исчисления функцию 
и
построить график.
