Условия дополняющей нежесткости Куна-Таккера

I'. Если - i < 0, то x_j 0,

если x_j 0, то - i = 0.

II'. Если _i(x₁,x₂,…, x_n) < b_i, то _i = 0,

если _i > 0, то _i(x₁,x₂,…, x_n) = b_i.

Условия I' и II' называются условиями дополняющей нежесткости. Рассмотрим их экономическую интерпретацию, исходя из прежней экономической постановки задачи ВП: x₁,x₂,…, x_n - план производства продукции, f (x₁,x₂,…, x_n) - прибыль от реализации продукции, _i(x₁,x₂,…, x_n) - потребность в ресурсе i по данному варианту производственной программы, x₁,x₂,…, x_n, b_i - лимит ресурса i.

Ранее нами было установлено, что 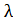_i есть оценка ресурса i по его влиянию на оптимальное значение целевой функции. Эта оценка равна производной = λ^o_i. Это справедливо для всех i.

Рассмотрим содержание соотношений II'. Положительность оценки λ^o_i (λ^o_i>0) указывает на то, что ресурс b_i в оптимальном плане используется полностью, то есть _i(x^o₁,x^o₂,…, x^o_n) = = b_i. Если ресурс используется не полностью, то есть _i(x^o₁,x^o₂,…, x^o_n) < b_i, то этот ресурс не является дефицитным, его оценка равна нулю: λ^o_i =0.

Аналогичным будет подход при рассмотрении содержания условий I'.

Продукт j целесообразно включить в план производства (x_j > 0) только в том случае, когда результатная оценка продукции совпадает с ее затратной оценкой i , то есть когда достигается баланс результата и затрат, связанных с малым выпуском продукции. Если же получаемый результат 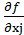(оценка продукции) меньше затрат ресурсов i , то включение в план производства продукта целесообразно (x_j = 0).

Рассмотрим формулировку условий дополняющей нежесткости применительно к задаче линейного программирования. Для такой задачи

Z = f (x₁,x₂,…, x_n) = 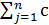_jx_j max,

_i(x₁,x₂,…, x_n) = 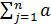_ijx_j ≤ b_i , i=1,2,…,m,

x_j ≥ 0, j=1,2,…,n,

= λ^o_i = y^o_i ; = c_j; = a_ij ;

i = 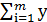^o_i a_ij .

Условия дополняющей нежесткости для задачи линейного программирования запишутся следующим образом.

Если 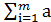_ijy^o_i > c_j, то x^o_j = 0;

если x^o_j > 0, то 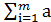_ijy^o_{i =} c_j;

если 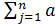_ijx^o_j < b_i, то y^o_i = 0;

если y^o_i > 0, то 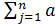_ijx^o_j = b_i.

Полученные соотношения были изучены нами еще в теории линейного программирования.

 

Теорема Куна-Таккера.

 

Введем понятие седловой точки функции многих переменных. Дана некоторая функция Q=Q(x₁,x₂,…, x_n, y₁, y₂,…, y_m) двух групп переменных x₁,x₂,…, x_n и y₁, y₂,…, y_m. Пусть по первой группе переменных функцию Q требуется максимизировать, по второй-минимизировать.

Определение. Точка (x^o₁,x^o₂,…, x^o_n, y^o₁, y^o₂,…, y^o_m) = (X_o,Y_o) называется седловой точкой функции Q, если в ней выполняется следующее неравенство:

Q(X, Y_o) ≤ Q (X_o,Y_o) ≤ Q(X_o,Y).

(4.1)

Рассмотрим следующую задачу выпуклого программирования:

Z = f (x₁,x₂,…, x_n) max,

(4.2)

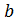₁(x₁,x₂,…, x_n) ≤ ₁,

₂(x₁,x₂,…, x_n) ≤ ₂,

- - - - - - - - - - - - - - -

_m(x₁,x₂,…, x_n) ≤ _m,

(4.3)

x₁ ≥ 0, x₂ ≥ 0, …, x_n ≥ 0.

 

Перейдем от этой задачи на условный экстремум к задаче на безусловный экстремум с помощью функции Лагранжа

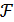(x₁,x₂,…, x_n, λ₁, λ₂,…, λ_m) = f (x₁,x₂,…, x_n) + _i (b_i – _i(x₁,x₂,…, x_n)).

(4.4)

Предположим, что найдена седловая точка функции Лагранжа

(x_o, λ_o) = (x^o ₁, x^o₂,…, x^o_n; λ^o₁, λ^o₂,…, λ^o_m).

Тогда справедливым будет следующее неравенство:

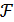(x, λ_o) ≤ 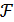(x_o, λ_o) ≤ 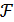(x_o, λ).

Задача отыскания точки (x_o, λ_o) из области определения функции (x, λ), удовлетворяющей неравенству (4.4), называется задачей о седловой точке.

Теорема. Точка x_o будет являться решением задачи ВП (4.1)-(4.3) тогда и только тогда, когда существует такая точка λ_o ≥ 0, что точка (x_o, λ_o) является седловой точкой функции Лагранжа 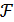(x, λ).