| (3.18) |
Z = f (x1,x2,…, xn) max,
 1(x1,x2,…, xn) ≤
1(x1,x2,…, xn) ≤ 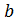 1,
1,
| (3.19) |
 2(x1,x2,…, xn) ≤
2(x1,x2,…, xn) ≤  2,
2,
- - - - - - - - - - - - - - -
 m(x1,x2,…, xn) ≤
m(x1,x2,…, xn) ≤  m,
m,
Путем добавления в левые части неравенств (3.31) неотрицательных переменных xn+1,xn+2,…, xn+m перейдем от ограничений-неравенств к ограничениям-равенствам
| (3.20) |
 1(x1,x2,…, xn) + xn+1=
1(x1,x2,…, xn) + xn+1= 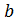 1,
1,
 2(x1,x2,…, xn) + xn+2=
2(x1,x2,…, xn) + xn+2=  2,
2,
- - - - - - - - - - - - - - - - - - - -
 m(x1,x2,…, xn) + xn+m=
m(x1,x2,…, xn) + xn+m=  m.
m.
Задача(3.18)-(3.20) является задачей ВП с ограничениями в виде равенств. Для ее решения, как и ранее, применим метод множителей Лагранжа
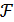 (x1,x2,…,xn+1,…, xn+m,λ1, λ2,…, λm) = f (x1,x2,…, xn) +
(x1,x2,…,xn+1,…, xn+m,λ1, λ2,…, λm) = f (x1,x2,…, xn) +  i (bi–
i (bi–  i(x1,x2,…,xn)- xn+i).
i(x1,x2,…,xn)- xn+i).
Вместо задачи (3.18)-(3.20) будем решать задачу на безусловный экстремум функции Лагранжа. Необходимое условие экстремума функции Лагранжа записывается так:
| (3.21) |
 = 0, j=1,2,…,n,
= 0, j=1,2,…,n,
| (3.22) |
 =0, i=1,2,…,m,
=0, i=1,2,…,m,
| (3.23) |
 =0, i=1,2,…,m.
=0, i=1,2,…,m.
Учитывая вид функции  , условия (3.21), (3.23) можно выразить следующим образом:
, условия (3.21), (3.23) можно выразить следующим образом:
| (3.24) |
 =
=  -
-  i
i  = 0,
= 0,
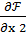 =
=  -
-  i
i  = 0,
= 0,
- - - - - - - - - - - - - - - - - - - - - - - - -
 =
=  -
-  i
i  = 0,
= 0,
 = b1 -
= b1 -  1(x1,x2,…, xn) - xn+1 = 0,
1(x1,x2,…, xn) - xn+1 = 0,
| (3.25) |
 = bm -
= bm -  m(x1,x2,…, xn) - xn+m =0.
m(x1,x2,…, xn) - xn+m =0.
Условия (3.22) с учетом неотрицательности переменных следует уточнить и записать в виде
| (3.26) |
 ∙ xn+i = 0, i=1,2,…,m.
∙ xn+i = 0, i=1,2,…,m.
Если экстремум функции 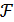 достигается внутри области допустимых решений (xn+i > 0), то в точке экстремума
достигается внутри области допустимых решений (xn+i > 0), то в точке экстремума  = 0, на границе области (xn+i = 0):
= 0, на границе области (xn+i = 0):  ≤ 0 в случае выпуклости
≤ 0 в случае выпуклости  ,
,  < 0 - при вогнутости
< 0 - при вогнутости  . Так как
. Так как  = -
= - 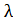 i, то условие (3.26) примет вид -λi xn+i = 0. Отсюда λi xn+i = 0, однако xn+i = bi–
i, то условие (3.26) примет вид -λi xn+i = 0. Отсюда λi xn+i = 0, однако xn+i = bi–  i(x1,x2,…,xn). Следовательно, получим
i(x1,x2,…,xn). Следовательно, получим
λi (bi–  i(x1,x2,…,xn)) = 0.
i(x1,x2,…,xn)) = 0.
В связи с тем, что  = -
= - 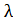 i ≤0, получим
i ≤0, получим  i ≥0. Окончательно условие (3.26) можно записать так:
i ≥0. Окончательно условие (3.26) можно записать так:
| (3.27) |
 i(x1,x2,…,xn)) = 0,
i(x1,x2,…,xn)) = 0,
bi–  i(x1,x2,…,xn) ≥ 0,
i(x1,x2,…,xn) ≥ 0,  i ≥0.
i ≥0.
Причем, если  i >0, то bi–
i >0, то bi–  i(x1,x2,…,xn) = 0, если
i(x1,x2,…,xn) = 0, если 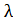 i =0, то bi–
i =0, то bi–  i(x1,x2,…,xn) ≥ или
i(x1,x2,…,xn) ≥ или 
 i(x1,x2,…, xn) ≤
i(x1,x2,…, xn) ≤  i.
i.
Для нахождения решения задачи (3.18)-(3.19) достаточно условий (3.24), (3.27). В них не входят переменные xn+i. Следовательно, можно и не вводить эти переменные в рассмотрение. Сразу можно было бы дял задачи (3.18)-(3.19) составлять функцию Лагранжа
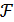 = f (x1,x2,…, xn) +
= f (x1,x2,…, xn) +  i (b i -
i (b i -  i (x1,x2,…, xn)).
i (x1,x2,…, xn)).
Тогда необходимое условие экстремума этой функции включаю бы, как и прежде, условие (3.24). Условие же (3.27) для этой функции стало бы таким:
 ≥0,
≥0,  i
i  =0,
=0,  i ≥0, i=1,2,…,m,
i ≥0, i=1,2,…,m,
где  = b1 -
= b1 -  1(x1,x2,…, xn).
1(x1,x2,…, xn).
Несколько усложняется решение задачи выпуклого программирования в случае ограничений в виде неравенств и ограничений неотрицательности.
Задача ВП в данном случае имеет вид
| (3.28) |
| (3.29) |
 1(x1,x2,…, xn) =
1(x1,x2,…, xn) =  1,
1,
 2(x1,x2,…, xn) =
2(x1,x2,…, xn) =  2,
2,
- - - - - - - - - - - - - - -
| (3.30) |
 m(x1,x2,…, xn) =
m(x1,x2,…, xn) =  m,
m,
xj ≥ 0, j=1,2,…,n.
| (3.31) |
| (3.32) |
 = 0, j=1,2,…,n,
= 0, j=1,2,…,n,
 i ≥0,
i ≥0,  i
i  =0,
=0,  ≥0,
≥0,
где  - функция Лагранжа вида
- функция Лагранжа вида
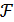 = f (x1,x2,…, xn) +
= f (x1,x2,…, xn) +  i (b i -
i (b i -  i (x1,x2,…, xn)).
i (x1,x2,…, xn)).
Если принять во внимание условие неотрицательности xj ≥ 0, j=1,2,…,n, то вместо равенств (3.31) следует пользоваться равенствами
xj  = 0, где xj ≥ 0,
= 0, где xj ≥ 0,  ≤ 0.
≤ 0.
С учетом вида функции Лагранжа  условия нахождения точка условного максимума задачи (3.28)-(3.30) можно будет записать так:
условия нахождения точка условного максимума задачи (3.28)-(3.30) можно будет записать так:
I группа условий:
 -
-  i
i  ≤ 0,
≤ 0,
( -
-  i
i  ≤ 0)xj = 0,
≤ 0)xj = 0,
xj ≥ 0, j=1,2,…,n;
II группа условий:
bi -  i (x1,x2,…, xn)≥0,
i (x1,x2,…, xn)≥0,
 i (
i ( i (x1,x2,…, xn) - b1) = 0,
i (x1,x2,…, xn) - b1) = 0,
xj ≥ 0, i=1,2,…,m.
Условия I и II называются условиями Куна -Таккера. Из совокупности этих условий выделим для более глубокого рассмотрения следующие отношения.






