5) (u(v))¢ = u¢(v)×v¢
Производные основных элементарных функций.
1) 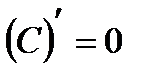
2) 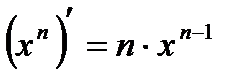
3) 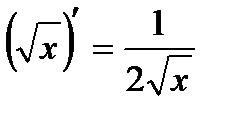
4) 
5) 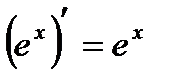
6) 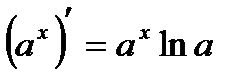
7) 
8) 
9) 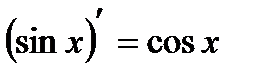
10) 
11) 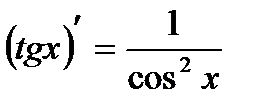
12) 
13) 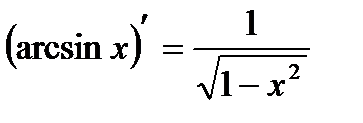
14) 
15) 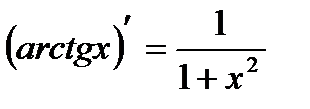
16) 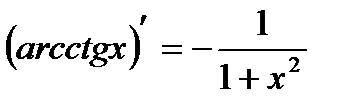
Производная сложной функции.
Теорема. Пусть y = f(x); u = g(x), причем область значений функции u входит в область определения функции f. Тогда
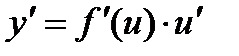
Производная показательно-степенной функции.
Функция называется показательной, если независимая переменная входит в показатель степени, и степенной, если переменная является основанием. Если же и основание и показатель степени зависят от переменной, то такая функция будет показательно – степенной.
Пусть u = f(x) и v = g(x) – функции, имеющие производные в точке х, f(x)>0.
Найдем производную функции y = uv. Логарифмируя, получим:
lny = vlnu
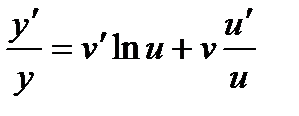

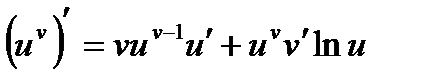
Производная функции заданной параметрически.
Дана функция 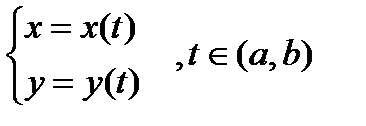 . Тогда ее производная будет
. Тогда ее производная будет
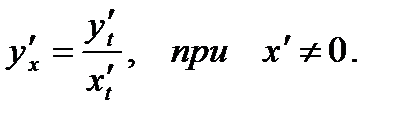
Производная неявно заданной функции.
Дана функция 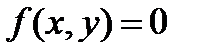 . Тогда ее производная будет
. Тогда ее производная будет
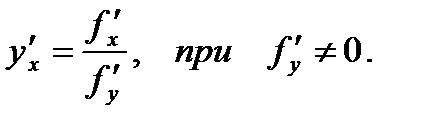
Пример. Найти производную функции 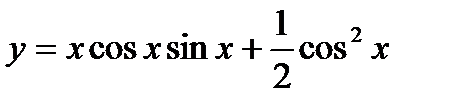 .
.
Сначала преобразуем данную функцию: 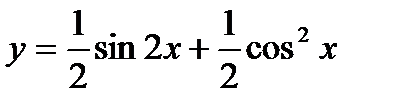

Пример. Найти производную функции  .
.
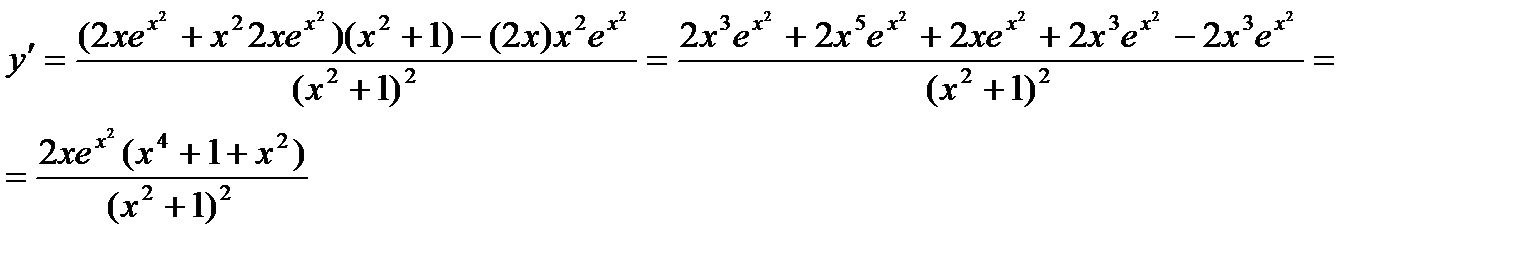
Пример. Найти производную функции 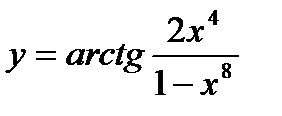

Пример. Найти производную функции  .
.
По полученной выше формуле получаем: 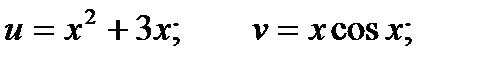
Производные этих функций: 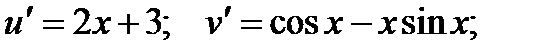
Окончательно:
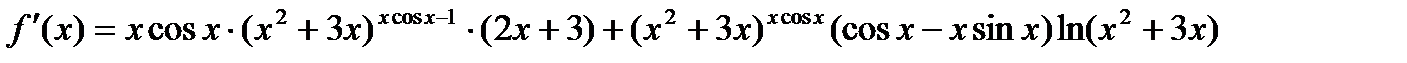
ВАРИАНТЫ
Числовых данных параметров т и п определяются по первым буквам фамилии и полного имени.
| А-В | Г-Е | Ж-И | К-М | Н-П | Р-Т | У-Х | Ц-Ш | Щ-Э | Ю-Я | ||
| Фамилия | т | ||||||||||
| Имя | п |
ЗАДАНИЯ
1. Найти производные 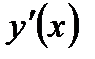 функций:
функций:
1) 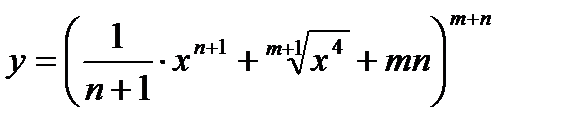 ;
;
2) 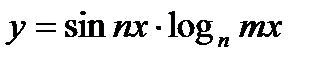 ;
;
3)  ;
;
4) 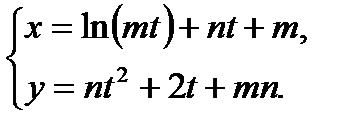
5) 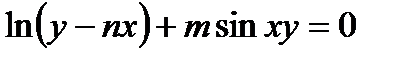 .
.
6)  ;
;
2. Найти производную третьего порядка функции  .
.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Ознакомиться с теоретическими сведениями.
2. Выбрать свой вариант согласно первым буквам фамилии и полного имени.
3. Записать исходные данные.
4. Решить задания.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Производная функции. Понятие о производных высших порядков.
2. Основные правила дифференцирования. Производная сложной функции.
3. Свойства производной функции. Производные основных элементарных функций.
4. Дифференцирование неявных, параметрически заданных и заданных в полярных координатах функций.
5.
6.
Практическая работа №8
Тема: Применение дифференциала и производной.
Цель: Научиться применять геометрический и физический смысл производной, вычислять предел правилом Лопиталя, применять дифференциал к приближенным вычислениям.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Геометрический смысл производной.
Определение. Если функция 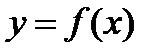 дифференцируема в точке
дифференцируема в точке 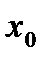 (т.е. если существует конечная производная
(т.е. если существует конечная производная  ), то уравнение касательной к графику функции в точке
), то уравнение касательной к графику функции в точке 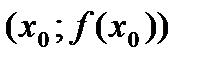 можно найти по следующей формуле:
можно найти по следующей формуле:  .
.
Определение. Если функция 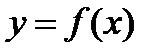 дифференцируема в точке
дифференцируема в точке 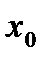 (т.е. если существует конечная производная
(т.е. если существует конечная производная  ), то уравнение нормали к графику функции в точке
), то уравнение нормали к графику функции в точке 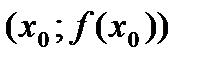 можно найти по следующей формуле:
можно найти по следующей формуле:  .
.
Механический смысл производной.
Если точка движется вдоль оси х и ее координата изменяется по закону x(t), то мгновенная скорость точки:  , а ускорение
, а ускорение 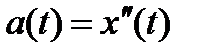 .
.
Правило Лопиталя.
Рассмотрим функции 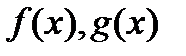 , которые бесконечно малыв некоторой точке k. Если существует предел их отношений
, которые бесконечно малыв некоторой точке k. Если существует предел их отношений 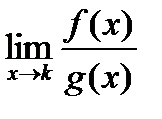 , то в целях устранения неопределённости
, то в целях устранения неопределённости 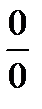 или
или  можно взять две производные – от числителя и от знаменателя. При этом:
можно взять две производные – от числителя и от знаменателя. При этом: 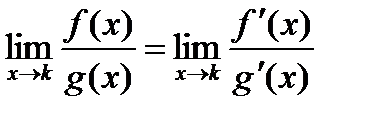 , то есть при дифференцировании числителя и знаменателя значение предела не меняется.
, то есть при дифференцировании числителя и знаменателя значение предела не меняется.
Применение правила Лопиталя к неопределённости вида  ,
,  ,
, 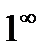 ,
, 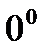 ,
,  так же возможно после некого преобразования функции в пределе.
так же возможно после некого преобразования функции в пределе.
Дифференциал функции.
Производную функции можно записать через дифференциал функции в виде:  . Откуда видно:
. Откуда видно: 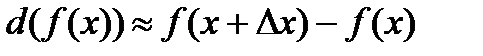 , что приращение функции приближенно равно дифференциалу функции при
, что приращение функции приближенно равно дифференциалу функции при 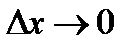 . Получим формулу для приближенных вычислений функции
. Получим формулу для приближенных вычислений функции
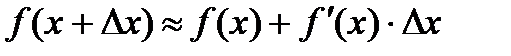 .
.
То есть идея формулы приближенных вычислений состоит в том, чтобы точное значение функции  заменить суммой значений
заменить суммой значений 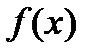 и
и 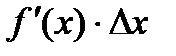 . Для этого необходимо начальное значение x 0 разделить на два слагаемых
. Для этого необходимо начальное значение x 0 разделить на два слагаемых 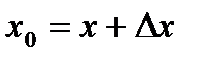 , причем так, чтобы значение функции от числа x легко вычислялось.
, причем так, чтобы значение функции от числа x легко вычислялось.
ВАРИАНТЫ
Числовых данных параметров т и п определяются по первым буквам фамилии и полного имени.
| А-В | Г-Е | Ж-И | К-М | Н-П | Р-Т | У-Х | Ц-Ш | Щ-Э | Ю-Я | ||
| Фамилия | т | ||||||||||
| Имя | п |
ЗАДАНИЯ
1. Составить уравнение нормали и касательной к кривой 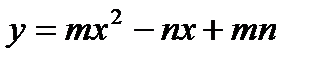 в точке (n–m; m+n).
в точке (n–m; m+n).
2. Материальная точка движется по закону 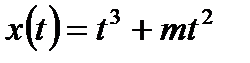 . Найти скорость и ускорение в момент времени t=n с.
. Найти скорость и ускорение в момент времени t=n с.
3. Найдите предел по правилу Лопиталя 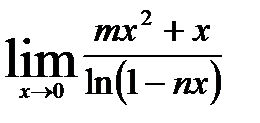 .
.
4. Вычислить приближенное значение функции  ,
, 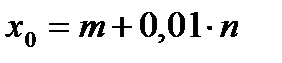 используя дифференциал функции.
используя дифференциал функции.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Ознакомиться с теоретическими сведениями.
2. Выбрать свой вариант согласно первым буквам фамилии и полного имени.
3. Записать исходные данные.
4. Решить задания.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Геометрический и физический смысл производной.
2. Теоремы Ролля, Лагранжа, Коши. Правило Лопиталя.
3. Применение формулы Тейлора в приближенных вычислениях.
4. Дифференциал функции, его геометрический смысл.
5. Полный дифференциал. Частные производные.
6. Приложение дифференциала функции к приближённым вычислениям.
7.
Практическая работа №9
Тема: Исследование функций и построение графиков.
Цель: Научиться исследовать функцию и строить ее график.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Схема исследования функций
Процесс исследования функции состоит из нескольких этапов. Для наиболее полного представления о поведении функции и характере ее графика необходимо отыскать:
1) Область существования функции. Это понятие включает в себя и область значений и область определения функции.
2) Точки разрыва. (Если они имеются).
3) Интервалы возрастания и убывания.
4) Точки максимума и минимума.
5) Максимальное и минимальное значение функции на ее области определения.
6) Области выпуклости и вогнутости.
7) Точки перегиба.(Если они имеются).
8) Асимптоты.(Если они имеются).
9) Построение графика.
Применение этой схемы рассмотрим на примере.
Пример. Исследовать функцию 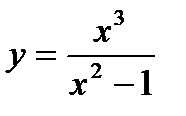 и построить ее график.
и построить ее график.
Находим область существования функции. Очевидно, что областью определения функции является область (-¥; -1) È (-1; 1) È (1; ¥).
В свою очередь, видно, что прямые х = 1, х = -1 являются вертикальными асимптотами кривой.
Областью значений данной функции является интервал (-¥; ¥).
Точками разрыва функции являются точки х = 1, х = -1.
Находим критические точки.
Найдем производную функции
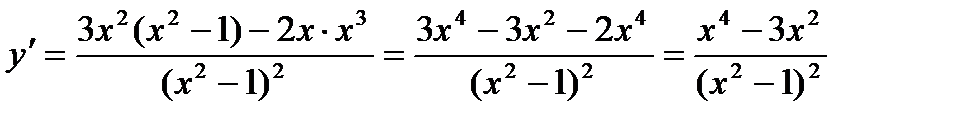
Критические точки: x = 0; x = -  ; x =
; x =  ; x = -1; x = 1.
; x = -1; x = 1.
Найдем вторую производную функции

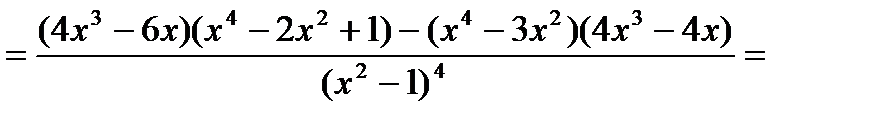
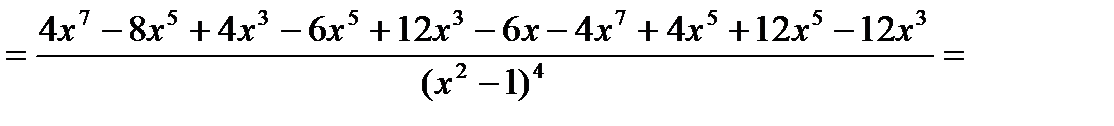
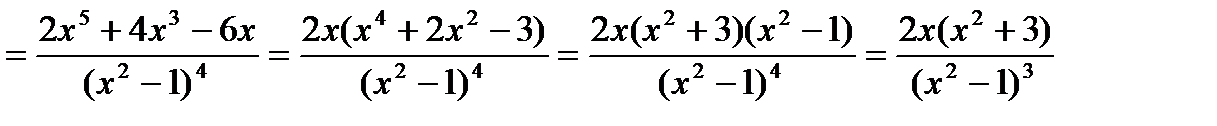 .
.
Определим выпуклость и вогнутость кривой на промежутках.
-¥ < x < - 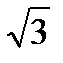
| -  < x < -1 < x < -1
| -1 < x < 0 | 0 < x < 1 | 1 < x < 
|  < x < ¥ < x < ¥
|
| y¢¢ < 0 | y¢¢ < 0 | y¢¢ > 0 | y¢¢ < 0 | y¢¢ > 0 | y¢¢ > 0 |
| кривая выпуклая | кривая выпуклая | кривая вогнутая | кривая выпуклая | кривая вогнутая | кривая вогнутая |
Находим промежутки возрастания и убывания функции. Для этого определяем знаки производной функции на промежутках.
-¥ < x < - 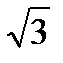
| -  < x < -1 < x < -1
| -1 < x < 0 | 0 < x < 1 | 1 < x < 
|  < x < ¥ < x < ¥
|
| y¢ > 0 | y¢ < 0 | y¢ < 0 | y¢ < 0 | y¢ < 0 | y¢¢ > 0 |
| функция возрастает | функция убывает | функция убывает | функция убывает | функция убывает | функция возрастает |
Видно, что точка х = -  является точкой максимума, а точка х =
является точкой максимума, а точка х =  является точкой минимума. Значения функции в этих точках равны соответственно 3
является точкой минимума. Значения функции в этих точках равны соответственно 3  /2 и -3
/2 и -3  /2.
/2.
Про вертикальные асимптоты было уже сказано выше. Теперь найдем наклонные асимптоты.


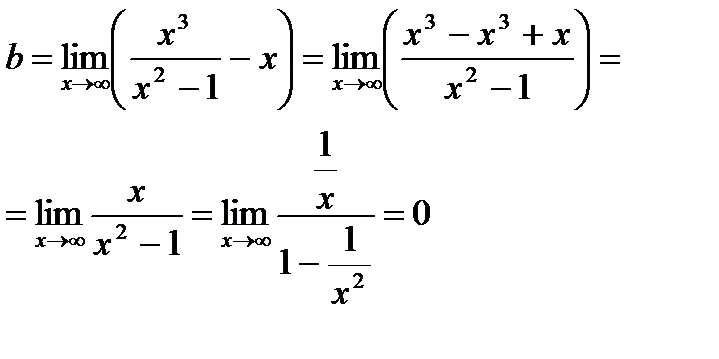
Итого, уравнение наклонной асимптоты – y = x.
Построим график функции.
ВАРИАНТЫ
Числовых данных параметров т и п определяются по первым буквам фамилии и полного имени.
| А-В | Г-Е | Ж-И | К-М | Н-П | Р-Т | У-Х | Ц-Ш | Щ-Э | Ю-Я | ||
| Фамилия | т | ||||||||||
| Имя | п |
ЗАДАНИЯ
Исследовать функцию и построить ее график.
а) 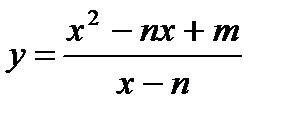 ; б)
; б) 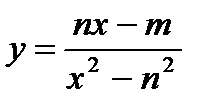
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Ознакомиться с теоретическими сведениями.
2. Выбрать свой вариант согласно первым буквам фамилии и полного имени.
3. Записать исходные данные.
4. Решить задания.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Применение первой производной к исследованию функции и построению графика.
2. Применение второй производной к исследованию функции и построению графика.
3.
4.
Практическая работа №10
Тема: Нахождение производной функции нескольких переменных.
Цель: Научиться находить частные производные и полный дифференциал функции нескольких переменных.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Частные производные первого порядка.
Пусть задана функция z = ƒ (х; у). Так как х и у – независимые переменные, то одна из них может изменяться, а другая сохранять свое значение. Дадим независимой переменной х приращение Δ х, сохраняя значение у неизменным. Тогда z получит приращение, которое называется частным приращением z по х и обозначается ∆ хz. Итак,
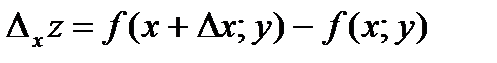 .
.
Аналогично получаем частное приращение z по у:
 .
.
Полное приращение Δ z функции z определяется равенством
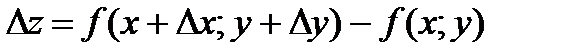 .
.
Если существует предел
 ,
,
то он называется частной производной функции z = ƒ (х; у) в точке М (х; у) по переменной х и обозначается одним из символов:
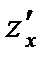 ,
, 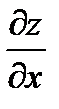 ,
,  .
.
Аналогично определяется и обозначается частная производная от z = ƒ (х; у) по переменной у:
 .
.
Таким образом, частная производная функции нескольких (двух, трех и больше) переменных определяется как производная функции одной из этих переменных при условии постоянства значений остальных независимых переменных. Поэтому частные производные функции ƒ (х; у) находят по формулам и правилам вычисления производных функции одной переменной (при этом соответственно х или у считается постоянной величиной).
Частные производные высших порядков.
Частные производные 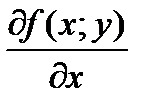 и
и  называют частными производными первого порядка. Их можно рассматривать как функции от (х; у) є D. Эти функции могут иметь частные производные, которые называются частными производными второго порядка. Они определяются и обозначаются следующим образом:
называют частными производными первого порядка. Их можно рассматривать как функции от (х; у) є D. Эти функции могут иметь частные производные, которые называются частными производными второго порядка. Они определяются и обозначаются следующим образом:
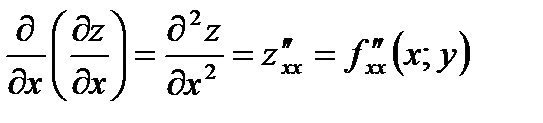 ;
;
 ;
;
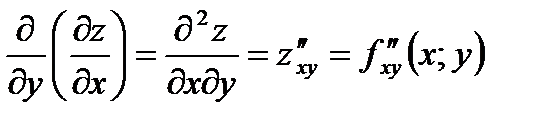 ;
;
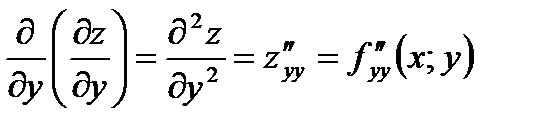 ;
;
Аналогично определяются частные производные 3-го, 4-го и т. д. порядков.
Частная производная второго или более высокого порядка, взятая по различным переменным, называетсясмешанной частной производной.
Полный дифференциал функции.
Пусть функция z = ƒ (х; у) определена в некоторой окрестности точки М (х; у) и имеет частные производные, то получаем формулу для вычисления полного дифференциала:
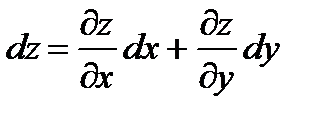 .
.
где 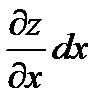 и
и  – частные дифференциалы функции z = ƒ (х; у).
– частные дифференциалы функции z = ƒ (х; у).
Арифметические свойства и правила исчисления дифференциалов функции одной переменной сохраняются и для дифференциалов функции двух (и большего числа) переменных.
Производная в данном направлении. Градиент функции.
Производная функции z = ƒ (х; у) в точке М (х; у) в направлении вектора  называется
называется 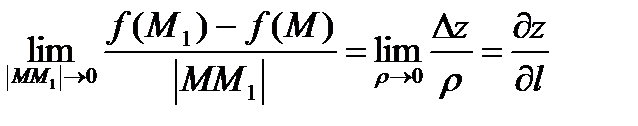 , где
, где 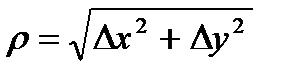 .
.
Если функция ƒ (х; у) дифференцируема, то производная в данном направлении вычисляется по формуле
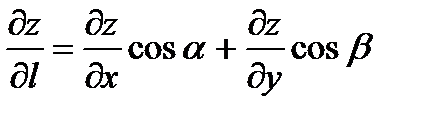 ,
,
где α, β – углы, образованные вектором 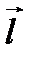 с осями Ox и Oy.
с осями Ox и Oy.
Производная по направлению 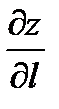 дает скорость изменения функции z в направлении вектора l.
дает скорость изменения функции z в направлении вектора l.
Определение. Градиентом функции z = ƒ (х; у) в точке М (х; у) называется вектор, выходящий из точки M и имеющий своими координатами частные производные функции z:
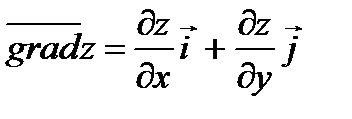 ;
; 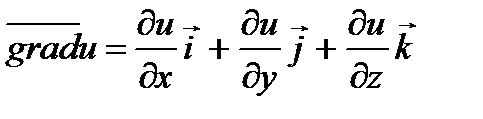 .
.
Градиент функции и производная в направлении вектора l связаны формулой  . Градиент указывает направление наибыстрейшего роста функции в данной точке.
. Градиент указывает направление наибыстрейшего роста функции в данной точке.
Уравнение касательной плоскости и нормали к поверхности в заданной точке.
Определение. Касательная плоскость к поверхности в точке М0 – это плоскость, содержащая касательные ко всем кривым, которые принадлежат данной поверхности и проходят через точку М0.
Если поверхность задана уравнением  (т.е. неявно), то уравнение касательной плоскости к данной поверхности в точке
(т.е. неявно), то уравнение касательной плоскости к данной поверхности в точке 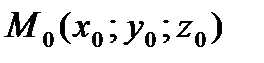 можно найти по следующей формуле:
можно найти по следующей формуле:
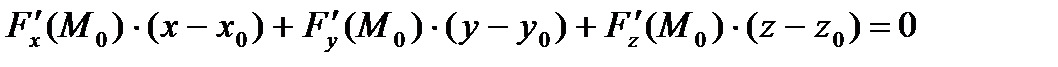 ,
,
где  – частные производные функции
– частные производные функции 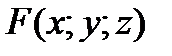 . При нахождении этих производных нужно руководствоваться правилами дифференцирования функции трёх переменных, то есть, при дифференцировании по какой-либо переменной, две другие буквы считаются константами
. При нахождении этих производных нужно руководствоваться правилами дифференцирования функции трёх переменных, то есть, при дифференцировании по какой-либо переменной, две другие буквы считаются константами
Определение. Нормаль к поверхности в точке М0 – это прямая, проходящая через данную точку перпендикулярно касательной плоскости.
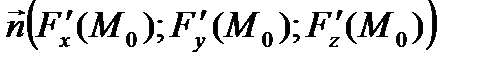 – это вектор нормали касательной плоскости, и он же – направляющий вектор нормальной прямой. Составим канонические уравнения нормали по точке М0 и направляющему вектору
– это вектор нормали касательной плоскости, и он же – направляющий вектор нормальной прямой. Составим канонические уравнения нормали по точке М0 и направляющему вектору 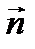 :
:  .
.
Экстремум функции двух переменных
Функция z = ƒ (х; у) имеет максимум (минимум) в точке М0 (х 0; у 0), если значение функции в этой точке больше (меньше), чем ее значение в любой другой точке М (х; у) некоторой окрестности точки M 0, то есть ƒ (х 0; у 0) > ƒ (х; у) (соответственно ƒ (х 0; у 0) < ƒ (х; у)) для всех точек М (х; у), принадлежащих этой окрестности. Максимум и минимум функции называется ее экстремумом. Точка M 0, в которой функция имеет экстремум, называется точкой экстремума.
Необходимое условие экстремума: если дифференцируемая функция z = ƒ (х; у) достигает экстремума в точке М0 (х 0; у 0), то ее частные производные первого порядка в этой точке равны нулю, то есть: 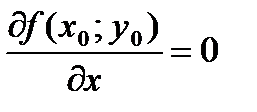 и
и 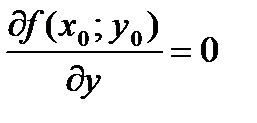 .
.






