Побудова епюр нормальних сил із врахуванням власної ваги стержня
Для заданого ступінчатого стержня (рис. 1.1а) побудувати епюру нормальних сил із врахуванням власної ваги стержня, якщo
Розв'язок
Викреслюємо розрахункову схему стержня в масштабі (рис. 1.1а). Розбиваємо його на ділянки, починаючи від незакріпленого кінця. Межами ділянок є перерізи, де прикладені зовнішні сили або змінюються розміри поперечного перерізу.
Для визначення нормальних сил, що діють на кожній ділянці стержня, використовуємо метод перерізів.
Нормальна сила вважається:
додатною, якщо вона викликає розтяг; від'ємною, якщо викликає стиск. Нормальна сила рівна сумі проекцій всіх зовнішніх сил та сил ваги стержня, що діють нижче перерізу, який розглядається, на вісь х, направлену вздовж осі стержня.
Вибираємо точку відліку на початку вільного кінця стержня. Умовно перерізаємо стержень в межах кожної ділянки, записуючи межі її зміни, а також загальний вираз для функції нормальної сили (рис. 1.1а):
ділянка І, 0<х <8м.
Значення нормальної сили на межах ділянки рівне:
ділянка II, 8 < х < 24m
ділянкаІІI 24 <х< 32m
ділянкаIV 32 < х < 40м
Будуємо епюри нормальних сил N.
| Змн. |
| Арк. |
| № докум. |
| Підпис |
| Дата |
| Арк. |
Задача №2
РОЗРАХУНОК НА МІЦНІСТЬ І ВИЗНАЧЕННЯ ПЕРЕМІЩЕНЬ ПРИ РОЗТЯГУ (СТИСКУ)
Для заданого ступінчатого стержня (рис. 1.4а) визначити розміри поперечного перетину на всіх його ділянках, виходячи з умови, що форма перетину круг; накреслити ескіз стержня; побудувати епюри дійсних нормальних напружень і поздовжніх переміщень, якщо, Е=2- 105МПа.
Розв'язок
Розбиваємо стержень на три ділянки I, II, III. Для кожної з ділянок визначаємо значення повздовжніх сил і будуємо епюру
З умови міцності на розтяг-стиск визначаємо необхідні площі поперечних перетинів стержня на кожній ділянці:
Діаметри стержня визначаємо за формулою:
Отримані результати заокруглюємо:.
На основі отриманих розмірів викреслюємо ескіз стержня (рис. 1.4в). Визначаємо дійсні площі поперечних перетинів стержня на кожній ділянці з врахуванням заокруглення їх діаметрів:
| Змн. |
| Арк. |
| № докум. |
| Підпис |
| Дата |
| Арк. |
Дійсні нормальні напруження рівні:
Використовуючи отримані значення, будуємо епюру нормальних напружень. Визначаємо повздовжні деформації кожної ділянки стержня:
За отриманими результатами будуємо епюру лінійних переміщень
| Змн. |
| Арк. |
| № докум. |
| Підпис |
| Дата |
| Арк. |
| Змн. |
| Арк. |
| № докум. |
| Підпис |
| Дата |
| Арк. |
Задача №3
Розрахунок статично невизначних систем
Для заданої стержневої системи (рис. 1.3а) визначити площі поперечних перерізів стержнів DЕ і КН, якщо відоме їхнє співвідношення Ade = ЗAkh, а також Р=50 кН; [σ] = 160 МПа. Брус АК вважати абсолютно жорстким.
Розв'язок
При навантаженні системи силою Р у стержнях DЕ і КН виникають осьові зусилля. Площі поперечних перерізів стержня при стиску визначаємо з умови міцності із допустимих напружень:
звідки

Для визначення зусиль в стержнях складаємо рівняння рівноваги бруса АК.
У системі є чотири невідомі зусилля та реакції (Nkh, Nde, Ву, Вх), а рівнянь рівноваги три, отже система 4-3=1 раз статично невизначна.

Складаємо додаткове рівняння - рівняння сумісності переміщень.
Після прикладання сили Р стержні DЕ і КН деформуються, і система займе положення, яке показане на рис.1.3в. З подібності трикутників DD’K i HH’K випливає, що
У даному випадку.
де ∆lkh I ∆lde - абсолютні деформації стержнів КН і DЕ. Деформації стержнів виразимо за законом Гука у вигляді:
Підставивши значення ∆lkh I ∆lde y вирази (1.5) і (1.4), отримаємо:
Підставивши Ade=3Akh і відповідно перетворивши, отримаємо:
У нашому випадку а=45° (рис. 1.3а), тоді
Розв'язуючи рівняння (1.3) і (1.6), визначаємо невідомі зусилля в стержнях:
Надалі рівняння (1.1) і (1.2) при розв'язуванні задачі не використовуються, так як невідомі зусилля в стержнях визначені, а за умовою задачі непотрібно визначати реакції в опорі В. Площу поперечного перерізу стержня КН визначаємо з умови міцності:
а площу поперечного перерізу стержня DE - з даного співвідношення:
Перевіряємо стержень DE на міцність:
Умова міцності забезпечена.
| Змн. |
| Арк. |
| № докум. |
| Підпис |
| Дата |
| Арк. |
Задача №4
Аналіз плоского напруженого стану.
Для заданого елемента (рис. 2.1а) визначити:
1) величину і напрямок головних напружень (графічно та аналітично);
2) величину тшах і положення площадки, де воно діє (графічно та аналітично);
3) відносні деформації в напрямку трьох головних напружень;
4) відносну зміну об'єму;
5) питому потенціальну енергію деформації;
6) розрахункові напруження, якщо матеріал елемента сталь Ст.6, чавун СЧ28-48 і порівняти їх з допустимими напруженнями, прийнявши пт=1,5, пв=2,5.
Розв’язок
Викреслюємо прямокутну систему координат στ, вісь σ проводимо паралельно більшому нормальному напруженню σа (рис. 2.16). У даній системі координат визначаємо точки, які відповідають напруженням на площадках α і β, точки Dα I Dβ. Так як ці точки зображають напруження, які діють на двох перпендикулярних площадках, то довжина Dα Dβ., є діаметром кола напружень. Точка перетину цього діаметра з віссю σ дає центр С кола. Точки А і В, де коло перетинає вісь σ, визначають величину головних напружень:
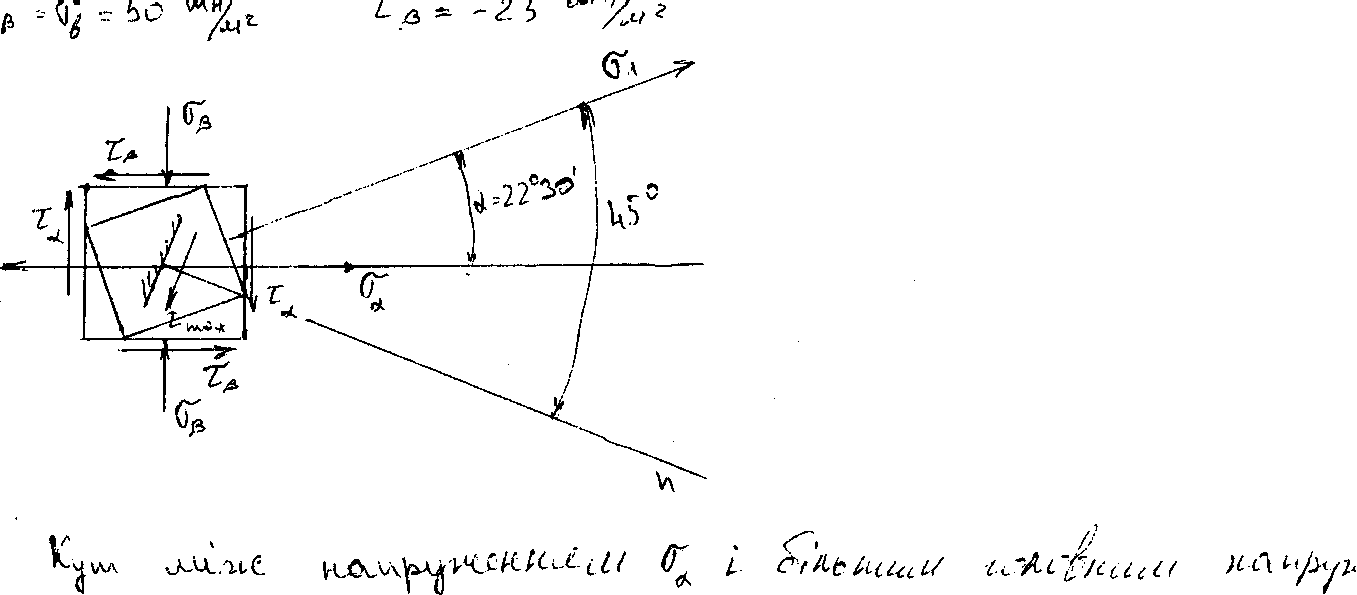
Кут між напруженням σа і більшим головним напруженням визначаємо за формулою:
| Змн. |
| Арк. |
| № докум. |
| Підпис |
| Дата |
| Арк. |
Максимальне дотичне напруження рівне:
Відносні деформації в напрямку головних напружень для стального елемента визначаємо за формулами:
Відносна зміна об'єму рівна:
Визначаємо питому потенціальну енергію деформації:
Допустимі напруження рівні:
а) для сталі Ст.6:
де σт=290МПа - границя текучості;
б) для чавуна СЧ28-48:
де σвр=280МПа, σвс=1000МПа - тимчасовий опір матеріалів відповідно при розтягу і стиску.
Для сталі Ст.6, перевірку на міцність можна проводити за третьою або четвертою теорією міцності. За третьою теорією міцності маємо:
Умову міцності забезпечено.
Для чавуна СЧ28-48 застосовуємо теорію міцності Мора, оскільки досліджуваний напружений стан матеріалу знаходиться між простим розтягом і простим стиском
Умову міцності для чавуна теж не забезпечено.
| Змн. |
| Арк. |
| № докум. |
| Підпис |
| Дата |
| Арк. |
Задача №5






