Термин «схема гибели и размножения» ведет начало от биологических задач, где численность популяции описывали схемой её изменения. Схема гибели и размножения очень часто встречается в теории массового обслуживания, поэтому полезно найти для неё предельные вероятности состояний.
Граф состояний для схемы гибели и размножения имеет вид:
Составим уравнения Колмогорова.
Для состояния S0: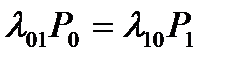 
.
Для состояния S1: 
,
учитывая, что 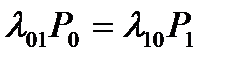, получим 
.
Для состояния S2: 
,
учитывая, что , получим 
.
И вообще, для состояния Sj: 
,
где j пробегает значения от 0 до (n-1).
Итак, финальные вероятности P0, P1, P2,…, Pn удовлетворяют системе:
Кроме того, надо учесть, что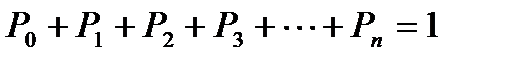 
.
Решим эту систему уравнений. Из первого уравнения следует 
Из второго уравнения получим 
.
Из третьего уравнения получим 
.
И вообще, для любого j+1 уравнения - 
.
Таким образом, все предельные вероятности выражены через P0
, 
, 
, 
,…
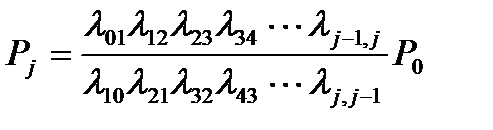. (9)
Обратим внимание на последние записи. В числителе стоит произведение всех интенсивностей, стоящих у стрелок, ведущих слева направо (сначала до состояния Sj), а в знаменателе – произведение всех интенсивностей, стоящих у стрелок, ведущих справа налево (сначала до состояния Sj).
Подставим предельные вероятности в равенство 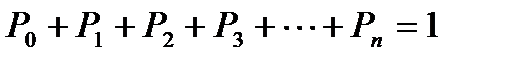, получим: 
.
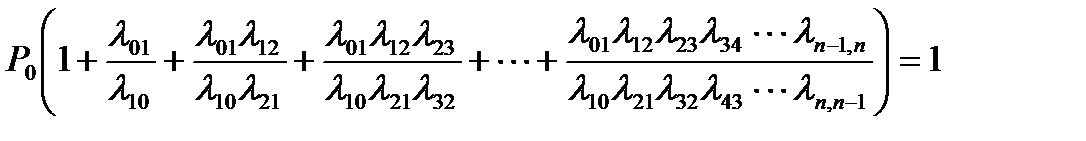Отсюда получим выражение для P0
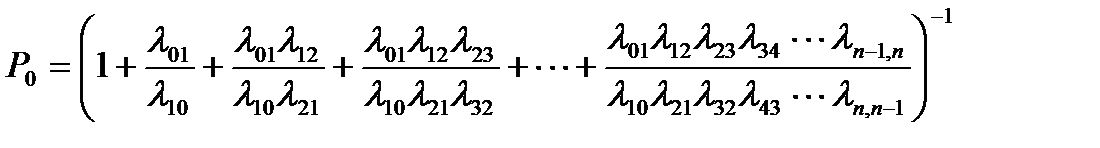. (10)
Затем по формулам (9) легко вычислить P1, P2, P3,, Pn-1, Pn.
Полученные формулы очень полезны при решении простейших задач теории массового обслуживания.
__________________________________________________________________
Формула Литтла.
Рассмотрим любую СМО и связанные с нею два потока событий: поток заявок, прибывающих в СМО, и поток заявок, покидающих СМО.
Если в системе установился предельный стационарный режим, то среднее число заявок, прибывающих в единицу времени, равно среднему числу заявок, покидающих её; оба потока имеют одну и туже интенсивность 
.
Обозначим: 
- число заявок, прибывающих в систему до момента 
;
- число заявок, покинувших систему до момента 
. Обе функции являются случайными и изменяются скачком (увеличиваются на единицу) в моменты прихода и ухода заявок.
Для любого момента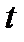 
разность 
есть не что иное, как число заявок, находящихся в системе.
|
Рассмотрим большой промежуток времени T и вычислим среднее число заявок, находящихся в системе. Оно будет равно
,
где Lсист – среднее число заявок, находящихся в системе, обслуживаемых или стоящих в очереди. Этот интеграл равен площади заштрихованных фигур. Фигура состоит из прямоугольников (высотой единица), основание равное времени пребывания заявки в системе: первой, второй, третьей и т. д.
Обозначим эти промежутки времени через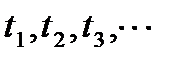 
Можно считать
,
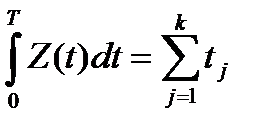где k - число заявок, пришедших за время T. Тогда
.
Разделим и умножим правую часть на интенсивность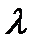 
, получим
.
Величина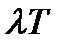 
- среднее число заявок, поступивших за время 
. Если разделить сумму всех переменных 
на среднее число 
, то получим среднее время пребывания заявки в системе 
. Итак,
.
Из последнего равенства следует формула Литтла:
. (11)
Формула Литтла гласит: среднее время пребывания заявки в системе равно среднему числу заявок в системе, делённому на интенсивность потока заявок.
Точно также выводится вторая формула Литтла, связывающая среднее время пребывания заявки в очереди 
и среднее число заявок в очереди 
. (12)
