Понятие простейшего потока событий.
Пусть имеется некоторая физическая система S, которая с течением времени меняет своё состояние, причем заранее неизвестном, случайным образом. Будем говорить, что в системе S протекает случайный процесс. Под «физической системой» можно понимать что угодно: техническое устройство, предприятие, живой организм, популяцию и т. д.
Случайный процесс, протекающий в системе, называется марковским, если для любого момента времени t0 вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент t0 и не зависят от того, когда и как система пришла в это состояние.
Если процесс марковский, то предсказывать можно учитывая настоящее состояние системы S0 и забыв о поведении системы при 
.Само состояние S0, разумеется, зависит от прошлого, но как только оно достигнуто, о прошлом можно забыть. В марковском процессе «будущее зависит от прошлого только через настоящее».
Пример марковского процесса: система S – счётчик Гейгера, на который время от времени попадают космические частицы.
В математическом моделировании систем и процессов большое значение имеют так называемые марковские случайные процессы с дискретными состояниями и непрерывным временем.
Процесс называется процессом с дискретными состояниями, если его возможные состояния S1, S2, S3,∙∙∙, Sn можно перечислить и переход системы из одного состояния в другое состояние происходит «скачком», мгновенно.
Процесс называется процессом с непрерывным временем, если моменты возможных переходов системы из одного состояния в другое не фиксированы, а неопределенны, случайны, переход может быть в любой момент времени.
Пример такого процесса: техническое устройство S состоит из двух узлов, каждый из которых в случайные моменты времени может выйти из строя, после чего мгновенно начинается ремонт узла, тоже продолжающийся заранее неизвестное случайное время. Возможные состояния системы можно перечислить:
S0 – оба узла исправны,
S1 – первый узел ремонтируется, второй исправен,
S2 – второй узел ремонтируется, первый исправен,
S3 – оба узла ремонтируются.
Построим граф состояний для рассматриваемого примера.
|
Стрелка из S0 в S1 означает переход в момент отказа первого узла; стрелка, направленная обратно, из S1 в S0 означает переход в момент окончания ремонта первого узла. Остальные стрелки объясняются аналогично.
Потоки событий.
Потоком событий называется последовательность однородных событий, следующих одно за другим в какие-то случайные моменты времени.
Например: поток вызовов на телефонную станцию; поток железнодорожных составов; поток частиц, попадающих на счётчик Гейгера; и т, д. Важнейшей характеристикой потока событий является его интенсивность 
- среднее число событий, приходящихся на единицу времени.
Поток событий называется стационарным, если его вероятностные характеристики не зависят от времени. В частности, интенсивность потока 
должна быть постоянной. На один промежуток времени может попасть больше событий, а на другой – меньше, но среднее число событий, приходящихся на единицу времени постоянно. Стационарность означает, что вероятность появления событий за время 
зависит лишь от длины интервала 
и не зависит от точки t отсчёта этого интервала.
Поток событий называется потоком без последействия (отсутствие последействия),если поступление заявки после момента времени t не зависит от того, когда и в каком количестве появлялись заявки до момента t.
То есть события появляются независимо друг от друга.
Поток событий называется ординарным, если события в нём появляются по одиночке, а не группами. Это условие означает, что одновременное появление двух и более событий маловероятно.
Поток событий называется простейшим (или стационарным пуассоновским), если он обладает сразу тремя свойствами: стационарен, ординарен и не имеет последействия. Название «простейший» связано с тем, что этот поток имеет наиболее простое математическое описание.
Можно показать, что для п р о с т е ш е г о потока вероятность 
появления ровно k событий за промежуток времени t вычисляется по формуле:
, (1)
т.е. вероятности распределены по закону Пуассона с параметром 
.
Эта формула отражает все свойства простейшего потока.
. Положив k= 0 и k= 1, можем вычислить вероятности не появления и появления одного события:
, 
.
Пример №1 На АТС поступает простейший поток вызовов. Среднее количество вызовов в течение часа равно m=72. Найти вероятности того, что за t=2 минутам: а) не придет ни одного вызова; б) придет хотя бы один вызов; в) придет не менее k=4 вызовов.
Решение. Так как поток простейший, то вероятность появления ровно k событий за промежуток времени t вычисляется по формуле Пуассона: с параметром , где 𝞴 – интенсивность потока (среднее число вызовов, приходящихся на единицу времени). В нашей задаче 
вызова в минуту. Параметр 
.
а) Найдем вероятность того, что за t=2 минутам не придет ни одного вызова. Для этого в формуле Пуассона надо положить k=0, получим 
, так как (0)!=1 и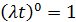 
. Тогда вероятность того, что за t=2 минутам не будет ни одного вызова равна 
. Далее вычисление выполняем с помощью таблицы значений 
.
Итак, вероятность того, что за t=2 минутам не придет ни одного вызова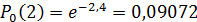 
.
б) Найдем вероятность того, что за t=2 минутам придет хотя бы один вызов. Вероятность появления одного или более одного вызова вычислим через вероятность противоположного события (не придет ни одного вызова):
Подставив в эту формулу t=2 и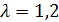 
, получим
.
Итак, вероятность того, что за t=2 минутам придет хотя бы один вызов
.
в) Найти вероятности того, что за t=2 минутам придет не менее k=4 вызовов.. Вероятность появления четырех и более четырех вызовов за время t вычислим также как вероятность противоположного события:
.
Вычислим 
, 
, 
.
Тогда 
.
Вероятность появления четырех и более четырех вызовов за время t=2
= 
.
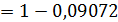
Итак, вероятность того, что за t=2 минутам придет не менее k=4 вызовов 
.
Пример №1 решен.
Интервал времени между поступлениями двух последовательных событий является случайной величиной. Обозначим эту случайную величину через T (Т= tj+1-tj).
Найдем функцию распределения случайной величины T
,
где 
- вероятность того, что случайная величина Т примет значение, меньшее, чем t; 
-вероятность противоположного события (т.е. за время t не появилось ни одного события). Согласно закону Пуассона (1) имеем
, (0!=1; t > 0)
откуда
, (t > 0). (2)
Найдем плотность распределения случайной величины Т
(t > 0) (3)
Можно показать, что математическое ожидание и дисперсия случайной величины Т имеют значения:
(4)
Таким образом, для простейшего потока с интенсивностью 
интервал времени Т между соседними событиями имеет так называемое показательное распределение с плотностью 
.
Показательным распределением описываются случайные величины в многочисленных задачах железнодорожного транспорта, элекротехники, радиосвязи, в теориях надежности, массового обслуживания, случайных процессов, например, время между прибытием поездов на сортировочные станции и отправления ми поездов со станций, время расформирования и формирования поездов, осмотра поездов бригадами техобслуживания, время ожидания в очереди, длительность телефонного разговора, время безотказной работы технического устройства и др.
Зная функцию 
, можно найти вероятность 
. Так как сумма вероятностей противоположных событий равна единице:
,
то 
.
Итак, вероятность того, что случайная величина Т примет значение не меньшее t, вычисляется по формуле: 
.
Чтобы найти вероятность 
события, состоявшего в том, что случайная величина наблюдается на интервале от 
до 
, воспользуемся свойством функции распределения вероятностей:
.
В расчётах, связанных с потоками событий, очень удобно пользоваться понятием «элемент вероятности». Рассмотрим на оси ot простейший поток событий с интенсивностью 
и произвольно расположенный элементарный (очень маленький) участок времени 
. Элементом вероятности называется вероятность попадания на участок 
хотя бы одного события потока. С точностью до бесконечно малых величин по сравнению с элемент вероятности равен
, (5)
т. е. элемент вероятности равен интенсивности потока, умноженной на длину элементарного участка времени.
