Состояний, из которых идут линии в данное j состояние, на интенсивность соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного j – состояния.
Таким образом, уравнения Колмогорова дают возможность найти все вероятности состояний как функции времени.
Поставим теперь вопрос: что будет происходить с вероятностями состояний при 
?
Предположим, что существуют пределы
где 
Если пределы существуют, то их называют предельными вероятностями состояний.
В теории случайных процессов доказывается, что если число состояний n системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое, то предельные вероятности существуют.
Предельную вероятность состояния Sj можно истолковывать как среднее относительное время пребывания системы в этом состоянии.
Например, система S имеет три состояния S1, S2, S3 и их предельные вероятности равны 
, 
и 
. Это значит, что в предельном стационарном режиме система в среднем две десятых времени проводит в состоянии S1, три десятых – в состоянии S2 и половину времени – в состоянии S3.
Если вероятности 
, 
постоянны, то их производные равны нулю. Уравнения Колмогорова (6) превращаются в систему линейных алгебраических уравнений:
Уравнения совпали. Но у нас есть еще одно уравнение, из формулы (7) имеем 
.
Итак, предельные вероятности состояний данной системы
определяются из системы алгебраических уравнений
. (8)
Решаем систему:
, 
, отсюда 
, тогда 
.
Пример №2. При работе электронного технического устройства возникают неисправности (сбои). Поток сбоев считается простейшим с интенсивностью 𝞴=0,5 сбоев в час. Если устройство дает сбой, то он немедленно обнаруживается, и обслуживающий персонал приступает к устранению неисправности (ремонту). Время ремонта распределено по показательному закону. Среднее время ремонта составляет τ=20 минут.
В начальный момент времени устройство исправно. Найти: а) вероятность того, что через час устройство будет работать; б) вероятность того, что за последующие Т= 6 часов устройство даст хотя бы один сбой; в) предельные вероятности состояний.
Решение. По условию задачи поток сбоев считается простейшим с интенсивностью 𝞴=0,5 сбоев в час и описывается законом Пуассона.
а) Найдем вероятность того, что через час устройство будет работать, то есть за время t= 1 час не появилось ни одного сбоя. Согласно закону Пуассона имеем
, 
.
Итак, вероятность того, что через час устройство будет работать, равна 
б) Найдем вероятность того, что за последующие Т= 6 часов устройство даст хотя бы один сбой. Событие «даст хотя бы один сбой» означает, что произойдет один сбой, или два, или три и так далее (в принципе неограниченное число сбоев).. Вычислим вероятность того, что за время Т =6 часам произойдет хотя бы один сбой в промежутке от 1 часа до 7 часов. Для этого воспользуемся формулой: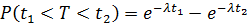 
.
Тогда 
=0,576.
Итак, вероятность того, что устройство даст хотя бы один сбой в промежутке от 1 часа до 7 часов, равна 0,95
в) Найдем предельные вероятности состояний.
Изобразим граф состояний электронного устройства:
Переход системы из состояния S0 в состояние S1 будем представлять так: как только появится сбой происходит мгновенный перескок системы из состояния S0 в состояние S1. Поток сбоев простейший с интенсивность 𝞴 сбоев в час.
После ремонта происходит мгновенный перескок системы из состояния S1 в состояние S0. Время ремонта распределено по показательному закону. Среднее время ремонта это математическое ожидание 
, для показательного закона 
, где µ - интенсивность (µ- среднее число ремонтов, приходящихся на единицу времени). По условию задачи М(Т) =τ=20 минутам= 
часа, тогда µ=3.
Система S имеет два состояния. Рассмотрим вероятности состояний. Вероятность того, что в момент t система будет в состоянии S0, обозначим через P0(t); а в состоянии S1 - через P1(t).
Используем правило составления уравнений Колмогорова:
в левой части каждого из них стоит производная j – го состояния;
в правой части – сумма произведений вероятностей всех тех состояний, из которых идут линии в данное j состояние, на интенсивность соответствующих потоков событий,
минус суммарная интенсивность всех потоков, выводящих систему из данного состояния в другие, умноженная на вероятность данного j – состояния.
Согласно этому правилу получим систему дифференциальных уравнений:
К этой системе дифференциальных уравнений добавим ещё одно уравнение
.
Одно уравнение лишнее. Нужно выбрать только два уравнения, проще такой:
Из второго уравнения 
, подставим в первое, получим:
.
Это линейное дифференциальное уравнение первого порядка. Решение будем искать в виде 
, подставим в уравнение
Преобразуем 
(⍟), полагаем 
.
Это дифференциальное уравнение с разделяющимися переменными.
; 
; 
; 
; 
.
Вернемся к уравнению (⍟), 
=µ; 
;
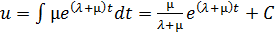, где С – произвольная постоянная.
Итак, общее решение уравнения
.
Определим произвольную постоянную С из начального условия: в начальный момент времени устройство исправно, то есть вероятность того, что система находилась в состоянии S0 , равна 1.
; 
; 
.
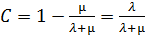Таким образом, 
.
Теперь вычислим вероятность второго состояния =
= 
.
Итак, решение системы 
Что будет происходить с вероятностями состояний при ?
При 
выражение 
, следовательно, предельные вероятности существуют и равны , .
Теперь подставим данные задачи 𝞴=0,5 и µ=3, получим:
, 
.
Итак, предельные вероятности состояний 
, 
.
Пример № 2 решен.
Элементы теории массового обслуживания.
Системы массового обслуживания будем коротко обозначать СМО. Примерами СМО могут служить: телефонные станции, ремонтные мастерские, билетные кассы, справочные бюро, магазины, парикмахерские и т. д.
Каждая СМО состоит из какого-то числа обслуживающих единиц (или «приборов»), которые будем называть каналами обслуживания. Каналами могут быть: линии связи на АТС, рабочие точки, кассиры, продавцы, лифты, автомашины и др.
СМО могут быть одноканальными и многоканальными.
Системы массового обслуживания делятся на типы по ряду признаков: СМО с отказами и СМО с очередью. Например, СМО с отказами – АТС. СМО с очередью подразделяются на разные виды: с ограниченной и неограниченной очередью. СМО бывают отрытоготипа и замкнутого типа. Например, СМО открытого типа: телефонные станции, билетные кассы, магазины и т. д. В открытой СМО поток заявок не зависит от того, в каком состоянии сама система; в замкнутой СМО - зависят. Например, ремонт станков осуществляет наладчик, поток заявок зависит от того, сколько их исправно и сколько ждёт наладки. Классификация СМО не ограничивается приведёнными разновидностями.
СМО предназначена для обслуживания какого-то потока заявок, поступающих в случайные моменты времени. Процесс работы системы массового обслуживания представляет собой случайный процесс с дискретными состояниями и непрерывным временем. Математический анализ работы СМО очень облегчается, если процесс этой работы – марковский. Для этого достаточно, чтобы все потоки заявок (событий), переводящие систему из одного состояния в другое состояние были простейшими.
