Основное назначение турбины 1 страница

– вращать вал электрогенератора

– вырабатывать мощность, которая для этого необходима.

Классификация паровых турбин (стандартные установки)

1. по назначению:

- энергетические (выработка электрической и тепловой энергии);

- промышленные (обслуживают крупные предприятия).

Электрические электростанции подразделяются на станции, которые вырабатывают только электричество (КЭС) и ТЭЦ.

В соответствии с назначением этих станций на них устанавливаются следующие типы турбин:

КЭС – турбины типа К – турбины конденсационного типа, имеющие обязательно конденсатор и служат для выработки электроэнергии.

Например, турбина типа К –300-240 (300 МВт – мощность; 240 атм. – давление острого пара на входе в турбину)

ТЭЦ:

1) турбины типа Т – теплофикационные турбины с 1 или максимум 2 регулируемыми отборами пара, причем этот отбор идет на нужды теплофикации (для горячей воды и для отопления). Имеет конденсатор.

2) турбина типа П. Применяется на промышленных электростанциях. Происходит отдача пара на нужды производства. Отдельно не используется. Не имеет конденсатор (весь пар уходит на предприятие).

3) турбина типа ПТ. Имеет конденсатор, 2 регулируемых отбора (промышленный и теплофикационный). Устанавливается на ТЭЦ если в районе есть предприятие, которому требуется пар для производства.

4) турбина типа Р – турбина с противодавлением. Не имеет конденсатора. Предназначена для выработки электроэнергии и теплоты, но она одна не может быть установлена на станции, только параллельно с турбинами, имеющие конденсатор, т.к. она может работать только по тепловому графику нагрузки (т.е. количество электроэнергии, которое она вырабатывает, зависит от тепловой потребности).

Например:

– турбина типа Т-250-240 – самая мощная турбина

– турбина типа ПТ/₁₃, где 13 – это давление промышленного отбора (давление теплофикационного отбора не указывается» 0,5 – 2,5 атм.

– турбина типа Р-50-130

2. по параметрам пара:

– докритические параметры (90,130 и 180 атмосфер)

– сверхкритические параметры (240 атм.)

 

Начальные параметры пара.

Давление перед турбиной, атм.	Параметры пара на выходе из п/г	Температура пара перед турбиной, 0С
Давление, атм.	Температура пара, 0С

 

Конечные параметры пара на выходе из турбины, имеющей конденсатор.

Р_к @ 0,03 – 0,05 атм.

t_к @ 23,8 – 32,5 ⁰С (t насыщения – 23 ⁰С)

 

3. по мощности:

– малой мощности (до 50 МВт)

– средней мощности (до 100 МВт)

– большой мощности (больше 100 МВт). Например: конденсационные 300, 500, 800, 1200 МВт; теплофикационные – 250 МВт.

4. конструктивные параметры:

– одноступенчатые и многоступенчатые турбины

– одноцилиндровые и многоцилиндровые турбины

– однокорпусные и многокорпусные

– двухвальные и одновальные

5. по движения пара:

– осевые турбины (аксиальные, т.к. движение пара параллельно оси вала) – применяется в нашей стране

– турбины радиального типа – движение пара перпендикулярно валу

6. по принципу действия пара:

– турбина активного типа

– турбина реактивного типа

– турбина смешенного типа

 

Турбинная ступень.

Она состоит из двух частей в следующей последовательности:

1.неподвижная часть (сопла)

2.вращающаяся часть (рабочее колесо)

 

Ступень активного типа – это ступень, в которой все расширение пара и связанное с ним ускорение парового потока происходит только в соплах, а в каналах рабочего колеса происходит преобразование кинетической энергии пара в механическую энергию вращения рабочего колеса, связанного с вращением вала.

Ступень реактивного типа – ступень, в которой расширение пара и ускорение потока происходит не только в соплах, но и в каналах рабочего колеса, где происходит преобразование кинетической энергии пара в механическую энергию ротора.

 

Лекция 7.

Конструктивный элемент.

В турбине есть подвижные и неподвижные части.

Неподвижная часть: диафрагма с соплами, лабиринтные уплотнения и корпус турбины. Лабиринтные уплотнения уменьшают зазор между вращающимися и неподвижными телами, тем самым, снижая потери пара.

Вращающаяся часть: диск, на который насажаны рабочие лопатки (рабочее колесо) и вал (ротор)

Рисунок 6.

1 – сопло (диафрагма)

2 – канал рабочее колесо (на диске)

3 – сопловая лопатка

4 – рабочая лопатка

с₀ – абсолютная входная скорость

с₁– абсолютная скорость выхода из сопла или входная скорость в канал рабочего колеса

с₂ – абсолютная скорость на выходе из каналов рабочего колеса

u – окружная скорость рабочего колеса

c₁²/2 – c₂²/ 2– энергия, вращающая вал рабочего колеса.

 

У каналов рабочего колеса есть относительная скорость:

w₁ – относительная скорость на входе в каналы рабочего колеса

w₂ – относительная скорость на выходе из каналов рабочего колеса

c₁ w₁

u₁

u

c₂ w₂

u₂

Рисунок 7.

 

Причем, верхний треугольник – это «Входной треугольник скоростей»,

 

c₁ w₁

α₁ β₁

u

Рисунок 8.

а нижний треугольник – «Выходной треугольник скоростей»

 

w₂

c₂

α₂ β₂

u

 

Рисунок 9.

где β₁ – угол входа пара в каналы рабочего колеса

β ₂ – угол выхода из каналов рабочего колеса

 

Для ступеней активного типа: w1 = w2 P1 = P2	Для активной и реактивной ступени характерно: с1 > с2
Для ступеней реактивного типа: w1 > w2 P1 < P2

 

Турбинная ступень: неподвижная часть ð вращающаяся часть

 

Компрессорная ступень (все наоборот, т.к. она потребляет работу): вращающаяся часть ð неподвижная часть.

 

Ступень активного типа:

 

Рисунок 10.

1 – корпус

2 – сопло

3 – лопатка

4 – диск

5 – лабиринтное уплотнение

6 – вал

 

P₀

c₁

w₁ w₂

c₂ P₁ P₂ c₂

 

 

Рисунок 11.

Ступень реактивного типа:

 

P₀

c₁ w₂

w₁

c₂

c₂ P₁

P₂

 

Рисунок 12.

Вектор абсолютной скорости:

с₁ = w₁ + u

с₂ = w₂ + u

 

Изменение давления в VS – диаграмме:

– активная ступень:

P₀

i t₀

P₁ = P₂

В

А

s

Рисунок 13.

где: – это адиабата

А – идеальное расширение

В – реальное расширение

 

с₁ w₂

w₁ c₂

α₁ β₁ β₂

u α₂ = 90^o u

Рисунок 14.

 

если отразить «выходной треугольник скоростей» относительно с₂ на «входной треугольник скоростей», то получим, что w₁= w₂ и β₁=β₂, следовательно расстояние между концами вектора с₁ и с₂ = 2u

 

2u/c₁ = cosα₁ ð u/c₁ = cosα₁/2

 

т.к. α₁ ≈ 20^о, то оптимальное отношение u/c₁ для активной ступени лежит в районе 0,5 более точно можно высчитать по формуле.

 

– реактивная ступень:

P₀

i t₀

P₁

P₂

i₁

В

i₂ А

s

Рисунок 15.

 

где А – идеальное расширение

В – реальное расширение

Р₁ à P₂ – расширение в каналах рабочего колеса

 

P, атм	ts = tнасыщ, °С	Интальпия жидкости	Интальпия пара	Теплота испарения, скрытая теплота парообразования
		i´ = h, ккал/кг	i´´, ккал/кг	r, ккал/кг
0,01	6,7	6,7	600,1	593,4
0,03	23,8	23,8	607,7	583,9
0,04	28,6	28,7	609,8	581,1
0,05	32,5	32,6	611,5	578,9
0,06	35,7	35,8	612,9	677,1
	99,1	99,1	638,5	539,4
	119,6	119,9	645,8	525,9
	158,1	159,3	657,8	498,5
	190,7	193,5	665,4	471,9
	301,9	323,6	655,1	331,5
	329,3		636,6	273,6
Критические показатели 229,5	374,2

 

Лекция 8.

Истечение в соплах (поведение потока).

1.Уравнение состояния:

PV=RT,

где P – давление [н/м²=Па], V – удельный объем [м³/кг], R – газовая постоянная, T – температура [ºК]. Зная две величины, можем определить третью, так как R – газовая постоянная.

2. Уравнения состояния (сплошности):

GV=FC,

Где G – секундная масса, секундный расход [кг/с], V – удельный объем [м³/кг], F – площадь поперечного сечения сопла [м²], С – скорость [м/с]. Предполагает секундный расход, равный const. G=FC/V= const.

ln G = ln F + ln C - ln V

0=dF/F +dC/C – dV/V

dF/F = dV/V – dC/C

G₁=G₂

F₁C₁/V₁ = F₂C₂/V₂

Сопла могут быть суживающиеся и расширяющиеся.

d F/F = 0 – сопло с постоянным сечением (труба);

d F/F > 0 – расширяющееся сопло;

d F/F < 0 – суживающееся сопло.

Все суживающиеся сопла – сопла дозвуковые, скорость истечения больше скорости звука. В соплах с постоянным сечением можно достигнуть скорости звука, но не превысить его. Для того, чтобы достигнуть скорости, превышающей скорость звука, сопло должно иметь следующую конфигурацию:

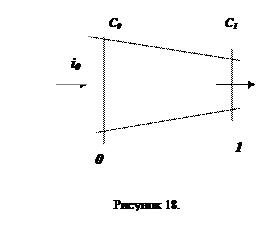
Рисунок 17. Конфигурация сверхзвукового сопла. Сопло Лаваля.

Критическое сечение – скорость потока, равная скорости звука, равная , Где k – показатель адиабаты.

3. Уравнение количества движения, которая вытекает из второго закона Ньютона.

F = ma = m (d c/ d t)

F d t = d (mc)

F d t = m d c,

где mc – количество движения, F d t – импульс действующих сил.

Изменение количества движения равно импульсу действующих сил.

-v d p = c d c= d (c²/2) – уравнение потока, - d p = d c, следовательно, уменьшается давление, когда скорость повышения и наоборот.

c²/2 – кинетическая энергия одного килограмма.

Для того чтобы увеличить скорость, необходимо снижать давление.

4. Уравнение сохранения энергии.

i1

i_o + c_o²/2 = i₁ + c₁²/2,

где i_o – потенциальная энергия на входе, c_o²/2 – кинетическая энергия на входе, i₁ - потенциальная энергия на выходе, c₁²/2 - кинетическая энергия на выходе.

При идеальном истечении:

i_o – i₁ = c₁²/2 – c₀²/2

Часто кинетическая энергия входного потока мала и ей пренебрегают.

c₁²/2 = i_o – i₁

В пренебрежении начальной скорости:

,

где i_o – i₁ – разность энтальпий.

Рисунок 19. Идеальное истечение

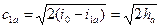, i₁ – скорость действительного истечения.

[i] = [Дж/кг], [c] = [м/с]

i_o – i₁ = h_д

h_c = i₁+i_1a – потери в соплах.

Потери в соплах.

h_c = h₁+h_д = c_1а²/2 - c₁²/2 = c_1а²/2 [1-(c₁/c_1а)²].

φ = c₁/c_1а – коэффициент сопла. 0, 97 <= φ <= 0,98 – чем больше φ, тем лучше, потери меньше.

h_c = h_а(1- φ²) – потери в сопловом аппарате.

Рисунок 20.

Потери на лопатках рабочего колеса.

Рассмотрим на примере реактивного типа.

Рисунок 21.

p₀ – давление перед ступенью;

p_i0 – энтальпия пара перед ступенью;

t₀ – температура пара перед ступенью (перед соплом);

p₁– давление пара на выходе из сопла или на входе в канал рабочего колеса;

p₂ – давление пара на выходе из канала рабочего колеса или давление на выходе из турбинной ступени;

h – теплоперепад.

h*_2a < h_2a

Общий перепад реактивной ступени, при действительном истечении, будет равен:

H_д = h ₁ +h ₂

H_а = h_1а+h_2а

H_д = h_1а+h*_2а

Отношение теплоперепада:

h_2a / (h _1а +h _2а) = ρ – реактивность (ступень реактивности)

ρ ≈ h_2a / (h _1а +h* _2а)

0,4<= ρ <=0,7

ρ=0,2 – активная ступень с небольшой реакцией.

 

Лекция 9.

Рисунок 22.

h_л=w_2a² / 2-w₂² / 2 – реальная работа колеса, w₂< w_2a

h_л=(w_2a² / 2)[1- (w₂ / w_2а) ²]

w₂ / w_2а=ψ

h_л=(w_2a² / 2)(1- ψ²) – реактивная и активная ступени

h_л=w_2a² /2- w₂² /2= w₂²/2 (w₂² / w_2а²-1)

h_л=w₂².2(1 / ψ²-1) – потери на соплах активной ступени

ψ=w₂. w₁

H_a – адиабатическое,

Рисунок 23.

Н_д – действительное.

 

Потери с выходной скоростью.

h_вых= с₂²/2 – потери выходной скорости [Дж/кг]

Векторы соотношения из треугольников скоростей.

Рисунок 24.

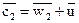
c_1u – проекция абсолютной скорости c₁, входной на направления окружной скорости.

c_1u= c₁ ∙ cos α₁, c_2u= c₂ ∙ cos α₂

w_1u= w₁ ∙ cos β₁, w_2u= w₂ ∙ cos β₂

+ c_1u +c_2u=w_1u +w_2u

c₁ ∙ cos α₁ +c₂ ∙ cos α₂ = w₁ ∙ cos β₁ +w₂ ∙ cos β₂

u c₁ ∙ cos α₁=1/2 (c₁² + u² –w₁²)

u c₂ ∙ cos α₂= -1/2 (c₂² + u² –w₂²)

u c₁ ∙ cos α₁ + u c₂ ∙ cos α₂=1/2 (c₁² -c₂² +w₂² -w₁²)

u w₁ cos β₁ + u w₁ cos β₁=1/2 (c₁² -c₂² +w₂² -w₁²)

u (cos α₁ +cos α₂)= 1/2 (c₁² -c₂² +w₂² -w₁²)

Мощность, развиваемая потоком пара на лопатках рабочего колеса.

Поворот и ускорение струи пара в каналах рабочего колеса в общем случае происходит в результате:

1) реактивных усилий, которые лопатки испытывают от струи пара. Это реактивное усилие лопаток, которое воздействует на струю пара.