Рассмотрим различные состояния системы:
x 0,0 – в системе нет никаких заявок;
x 0, j – в системе имеется j заявок, обладающих приоритетом 1 (j = 1, 2,...), и нет заявок, обладающих приоритетом 2; из этих j заявок одна обслуживается и j –1 заявок ожидают в очереди;
x 0, i – в системе имеется i заявок, обладающих приоритетом 2 (i = 1, 2,...), и нет заявок, обладающих приоритетом 1; из этих i заявок одна обслуживается и i– 1 заявок находятся в очереди;
xij – в системе имеется i заявок, обладающих приоритетом 2 (i = 1,2,...), и j заявок, обладающих приоритетом 1 (j =1,2,...); из i заявок, обладающих приоритетом, одна заявка обслуживается, а остальные i– 1 ожидают в очереди; до тех пор, пока все заявки, обладающие приоритетом, не будут обслужены, заявки, не обладающие приоритетом, не обслуживаются
Граф системы
Система уравнений
Пуассо́на пото́к (проце́сс) — поток однородных событий, для которого число событий в интервале А не зависит от чисел событий в любых интервалах, не пересекающихся с А , и имеетПуассона распределение с параметром Λ(А) . В теории случайных процессов описывает количество наступивших случайных событий, происходящих с постоянной интенсивностью.
| Содержание [убрать] · 1 Классификация o 1.1 Простой процесс Пуассона o 1.2 Сложный (обобщённый) Пуассоновский процесс · 2 Свойства · 3 Критерий · 4 Информационные свойства o 4.1 ЦПТ · 5 Применение · 6 Примечания · 7 См. также |
Вероятностные свойства потока Пуассона полностью характеризуются функцией Λ(А) , равной приращению в интервале А некоторой убывающей функции. Чаще всего поток Пуассона имеет мгновенное значение параметра λ(t) — функцию, в точках непрерывности которой вероятность события потока в интервале [t,t+dt] равна λ(t)dt . Если А — отрезок [a,b] , то
Поток Пуассона, для которого λ(t) равна постоянной λ , называется простейшим потоком с параметром λ .[1]
Потоки Пуассона определяются для многомерного и вообще любого абстрактного пространства, в котором можно ввести меру Λ(А) . Стационарный поток Пуассона в многомерном пространстве характеризуется пространственной плотностью λ . При этом Λ(А) равна объему области А , умноженному на λ .
Править]Классификация
Различают два вида процессов Пуассона: простой (или просто: процесс Пуассона) и сложный (обобщённый).
Править]Простой процесс Пуассона
Пусть λ > 0. Случайный процесс 
называется однородным Пуассоновским процессом с интенсивностью λ, если
1. X 0 = 0 почти наверное.
2. { Xt } — процесс с независимыми приращениями.
3. 
для любых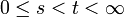 
, где P(λ(t − s)) обозначает распределение Пуассона с параметром λ(t − s).
