СМО с отказами и полной взаимопомощью для пуассоновских потоков. Граф, система уравнений, расчетные соотношения

СМО с отказами (классическая система Эрланга). Граф, система уравнений, расчетные соотношения.

x ₀ – все каналы свободны, ни одна заявка не обслуживается;

x ₁ – занят ровно один канал (какой – не важно), обслуживается одна заявка;

x_k – занято ровно k каналов (каких именно – не важно), обслуживается k заявок;

x_n – все n каналов заняты, обслуживается n заявок.

 

Система уравнений

 

 

Основные характеристики определяются следующим образом:

1. Вероятность того, что занято ровно k каналов,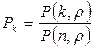

2. Среднее число занятых каналов: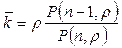

3. Вероятность обслуживания заявки (относительная пропусканная способность системы): 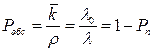, где – плотность потока обслуженных заявок (абсолютная пропускная способность системы)

4. Вероятность того, что канал (любой) занят: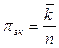

5. Вероятность того, что система полностью загружена:

6. Среднее время занятости канала: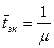

7. Среднее время простоя канала: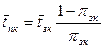

8. Среднее время пребывания заявки в системе:

 

 

СМО с отказами для произвольных потоков. Граф, система уравнений, расчетные соотношения.

 

 

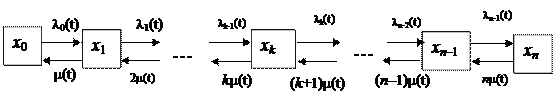
Система уравнений

 

 

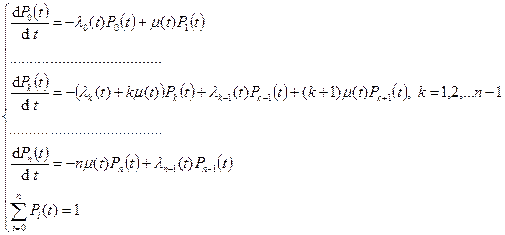
Математическая модель процесса «гибели и размножения». Граф, система уравнений.

Граф процесса

 

Система дифференциальных уравнений для вероятностей состояний процесса гибели и размножения

 

,

............................................

,

............................................

,

.

 

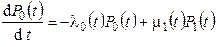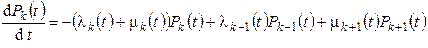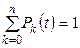Для интегрирования этой системы дифференциальных уравнений нужно задать начальные условия

Р ₀(0); Р ₁(0),..., Р_n (0); .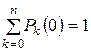

 

Система алгебраических уравнений для вероятностей состояний простейшего процесса гибели и размножения

 

–λ ₀ Р ₀ + μ₁ Р ₀ = 0,

.…………………

–(λ _k + μ _k) Р_k + λ _kР_{k –1}+ μ _{k +1} Р_{k +1} = 0 (k = 1,2,..., n –1),

.………………….

λ _{n –1} Р_{n –1} – μ _n Р_n = 0.

.

 

 

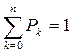Математическая модель процесса «гибели». Граф, система уравнений.

 

Граф процесса

 

 

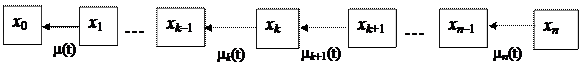Система дифференциальных уравнений для вероятностей состояний процесса гибели

 

,

............................................

,

............................................

,

.

 

 

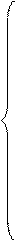
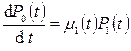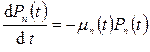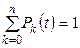Математическая модель процесса «размножения». Граф, система уравнений.

Граф процесса

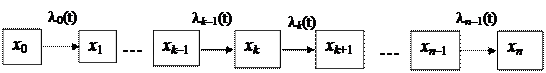Система дифференциальных уравнений для вероятностей состояний процесса размножения

,

............................................

,

............................................

,

.

 

 

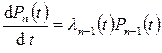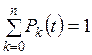СМО с отказом и частичной взаимопомощью для пуассоновских потоков. Граф, система уравнений, расчетные соотношения.

Граф системы

 

 

Система уравнений

 

 

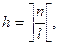где n – число каналов обслуживания, l – число взаимопомогающих каналов

 

Расчетные соотношения:

 

1)

Где ;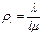

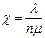
2)

Где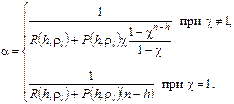

 

3)

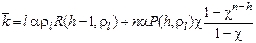
4)

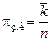
СМО с отказом и частичной взаимопомощью для произвольных потоков. Граф, система уравнений, расчетные соотношения.

 

Граф системы

 

Система уравнений

 

 

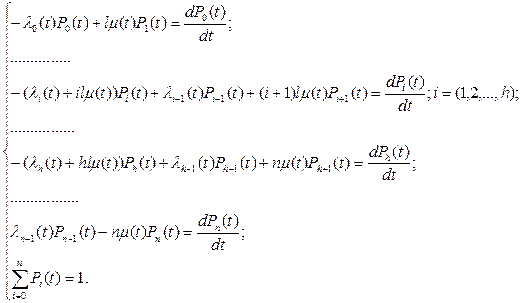
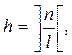где n – число каналов обслуживания, l – число взаимопомогающих каналов

 

СМО с отказами и полной взаимопомощью для пуассоновских потоков. Граф, система уравнений, расчетные соотношения.

Граф системы

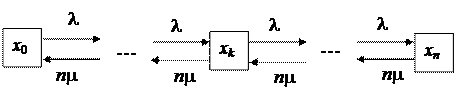Система уравнений:

 

–λ Р ₀ + n μ Р ₁=0,

.………………

–(λ + n μ) Р_k + λ Р_{k –1} + n μ Р_{k +1}=0 (k = 1,2,..., n –1),

……………....

λ Р_{n –1} – n μ Р_n =0.

 

 

Расчетные соотношения:

 

1) .

 

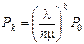2) Вероятность обслуживания заявки определяется из выражения

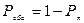
3) Среднее число занятых каналов 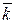определяется так:

 

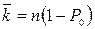
4) Для этой системы вероятность того, что любой отдельный канал будет занят, равна вероятности того, что все каналы будут заняты.

.

 

5) Среднее время простоя

.

 

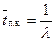6) Среднее время занятости канала

.