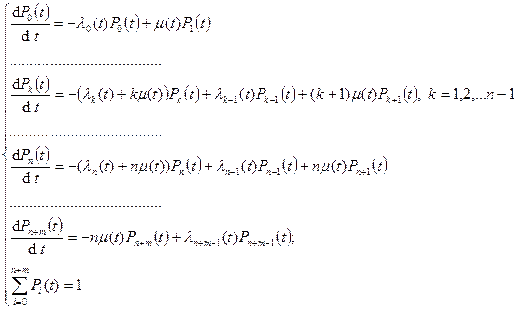СМО с отказами и полной взаимопомощью для произвольных потоков. Граф, система уравнений, расчетные соотношения

 

 

Граф системы

 

 

 

Система уравнений

 

 

 

СМО с отказами для случайного числа обслуживающих потоков векторная модель для пуассоновских потоков. Граф, система уравнений.

СМО представим в виде вектора , где k_m – число заявок в системе, каждая из которых обслуживается m приборами; L = q _max – q _min+1 – число входных потоков.

 

Если заявка принимается на обслуживание и система переходит в состояние с интенсивностью λ _m.

При завершении обслуживания одной из заявок система перейдет в состояние, в котором соответствующая координата имеет значение, на единицу меньшее, чем в состоянии , = , т.е. произойдет обратный переход.

Пример векторной модели СМО для n = 3, L = 3, q _min = 1, q _max = 3, P (m) = 1/3, λ_Σ = λ, интенсивность обслуживания прибора – μ.

По графу состояний с нанесенными интенсивностями переходов составляется система линейных алгебраических уравнений. Из решения этих уравнений находятся вероятности Р (), по которым определяется характеристики СМО.

 

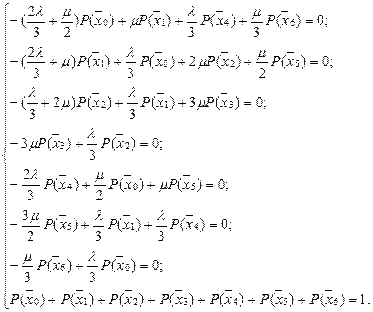
СМО с бесконечной очередью для пуассоновских потоков. Граф, система уравнений, расчетные соотношения.

 

 

Граф системы

…

 

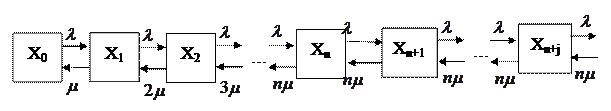
Система уравнений

 

 

 

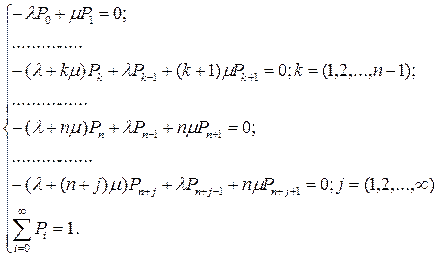
СМО с бесконечной очередью для произвольных потоков. Граф, система уравнений, расчетные соотношения.

 

 

Граф системы

 

μn(t)

λn+j(t)

λn+j-1(t)

λn+1(t)

λn(t)

λn-1(t)

λ2(t)

λ1(t)

…

 

Где - суммарная интенсивность обслуживания для k каналов

 

 

Система уравнений

 

 

 

СМО с бесконечной очередью и частичной взаимопомощью для пуассоновских потоков. Граф, система уравнений, расчетные соотношения

 

Граф системы

 

 

Система уравнений

 

 

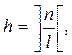где n – число каналов обслуживания, l – число взаимопомогающих каналов

 

СМО с бесконечной очередью и частичной взаимопомощью для произвольных потоков. Граф, система уравнений, расчетные соотношения.

 

Граф системы

 

 

Система уравнений

 

 

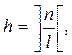где n – число каналов обслуживания, l – число взаимопомогающих каналов

 

СМО с бесконечной очередью и полной взаимопомощью для пуассоновских потоков. Граф, система уравнений, расчетные соотношения.

 

Граф системы

 

…

 

Система уравнений

–λ Р ₀ + n μ Р ₁=0,

.………………

–(λ + n μ) Р_k + λ Р_{k –1} + n μ Р_{k +1}=0 (k = 1,2,..., n –1),

……………....

-(λ+ n μ) P_n + λ Р_{n –1} + n μ Р_n+1 =0,

……………….

-(λ+ n μ) P_n+j + λ Р_{n+j –1} + n μ Р_n+j+1 =0, j=(1,2,….,∞)

 

.

 

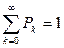СМО с бесконечной очередью и полной взаимопомощью для произвольных потоков. Граф, система уравнений, расчетные соотношения.

Граф системы

	λn+j-1(t)		λn+j(t)

…

Система уравнений

 

 

 

СМО с конечной очередью для пуассоновских потоков. Граф, система уравнений, расчетные соотношения.

 

Граф системы

 

 

Система уравнений

 

 

Расчетные соотношения:

 

,

Где ; .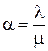

 

 

вероятность обслуживания заявки

 

 

 

среднее число занятых каналов

 

 

 

Вероятность того, что система полностью загружена

 

СМО с конечной очередью для произвольных потоков. Граф, система уравнений, расчетные соотношения.

Граф системы

 

Система уравнений