Поверхностью второго порядка называется множество всех точек пространства,
координаты которых удовлетворяют алгебраическому уравнению второй степени
a 11 x 2 + a 22 y 2 + a 33 z 2 + 2 a 12 xy + 2 a 13 xz + 2 a 23 yz + 2 a 10 x + 2 a 20 y + 2 a 30 z + a 00 = 0, где
коэффициенты a 11, a 22, a 33, a 12, a 13, a 23, a 10, a 20, a 30, a 00 − действительные числа, причем a 11,
a 22, a 33, a 12, a 13, a 23 не равны нулю одновременно.
| Название поверхности | Каноническое уравнение | Схематическое изображение | ||||||||||||||||||||||||
| Эллипсоид (в частности, эллипсоид вращения и сфера) |
| 
| ||||||||||||||||||||||||
| Однополостный гиперболоид |
| 
| ||||||||||||||||||||||||
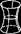
| Двухполостный гиперболоид |
| 
| ||||||||||||||||||||||||
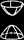
| Конус второго порядка |
| 
| ||||||||||||||||||||||||
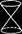
| Эллиптический параболоид |
| 
| ||||||||||||||||||||||||
| Гиперболический параболоид |
| 
| ||||||||||||||||||||||||
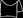
| Эллиптический цилиндр |
| 
| ||||||||||||||||||||||||
| Гиперболический цилиндр |
| 
| ||||||||||||||||||||||||
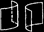
| Параболический цилиндр |
| 
| ||||||||||||||||||||||||
| Пара пересекающихся плоскостей |
| 
| ||||||||||||||||||||||||
| Пара параллельных плоскостей |
| 
| ||||||||||||||||||||||||
| Пара совпадающих плоскостей |
| 
| ||||||||||||||||||||||||
| Мнимый конус второго порядка с действительной вершиной (0;0;0) |
| |||||||||||||||||||||||||
| Пара мнимых плоскостей (пересекающихся по действительной прямой) |
|
29)Частное и полное приращение функции двух переменных.
Частные приращения:
Z=f(M) опр.на {М} и пусть М(Х,У) принадлежит {М},придадим переменной Х приращение ∆Х, так что (х+∆Х;У) принадлежит {М},тогда ∆хZ=f(х+∆Х;У)-f(х;у) называется приращением переменной Х.
Аналогично ∆уZ=f(х;у+∆у)-f(х;у) приращение z по у
∆Z=f(x+∆x;y+∆Y)-f(x;у)-полное приращение функции.
30) Непрерывность функции двух переменных
Пусть функция z = f (x,y) определена в точке M0(x0y0) и её окрестности.
Функция называется непрерывной в точке M0(x0y0), если
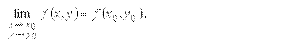
Если функция f (x,y) непрерывна в точке M0(x0y0), то
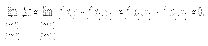
Поскольку
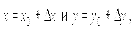
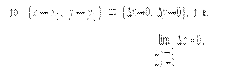
То есть, если функция f (x,y) непрерывна в точке M0(x0y0), то бесконечно малым приращениям аргументов в этой области соответствует бесконечно малое приращение Δz функции z.
Основные свойства непрерывных функций двух переменных:
1)Если Z=f(M) непрерывна на замкнутом ограниченном множестве, тоZ-ограниченная функция,т.е.ƎR не равно ∞,где|f(M)| < R на этом множестве.
2)если Z=f(M) непрерывна на замкнутом ограниченном множестве,то f(M) достигает своей верхней и нижней границы.
3)Если z=f(M) непрерывна на замкнутом ограниченном множестве,то Z принимает все промежуточные значения между своей верхней и нижней границей.
31) Частные производные и дифференцируемость функций двух переменных.
Если Ǝ 
, то его называют частной производной z по x обозначают: Zx; 
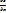
Дифференцируемость функций двух переменных.
Рассмотрим функцию z = f(x,y), имеющую в точке Р0(х0,у0) частные производные f¢x(х0,у0) и f¢у(х0,у0). Перейдём от точки Р0 к точке R0(x0+Dx,y0+Dу), придавая переменным х и у в точке Р0 произвольные приращения Dx и Dу, соответственно. При этом функция в точке Р0 получит приращение:
Df(х0,у0) = f(x0+Dx,y0+Dy) – f(x0,y0) = f(R0) – f(P0).
Определение. Если приращение функции f(x,y) можно представить в виде:
Df(х0,у0) = f¢x(х0,у0)Dx + f¢у(х0,у0)Dу + a(Dx;Dу) Dx + b(Dx;Dу)Dу,
Где 
то функция называется дифференцируемой в точке Р0(х0,у0). Сумма первых двух слагаемых в правой части равенства (1) называется дифференциалом функции f(x,y) в точке Р0 и обозначается df(x0,y0): df(x0,y0) = f¢x(х0,у0)Dx + f¢у(х0,у0)Dу.
Если точка, в которой вычисляется дифференциал не существенна, его принято обозначать просто df. Из определения следует, что дифференциал представляет собой главную часть приращения функции, линейную относительно приращений её аргументов. Полагая поочерёдно f(x,y) = х и f(x,y) = у, получим, что дифференциалы dх и dy независимых аргументов функции х и у равны соответственно Dx и Dу.
32)Необходимые и достаточные условия дифференцируемости функции двух переменных:
Необходимые:
Если функция Z=f(M) дифференцируема в т.М,то она непрерывна в этой точке
Если функция Z=f(M) дифференцируема в т.М,то она в этой точке имеет частные производные.
Достаточные:
Если функция и ее частные производные непрерывны в т.М,то эта функция дифференцируема в точке.
33)Дифференцирование неявно заданной функции.
F=(x,y)=0
Если Ǝ F’, и F’y, то Y’x=- 
34)Дифференцирование от сложной функции:
Пусть z=f(M)=f(x,y)
X(t),y(t)
Ǝ производная x’(t) и y’(t)
Если Z=f (x(t),y(t)) определяема и дифференцируема,то
= 
+ 
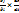35)Частные дифференциалы.Полный дифференциал функции двух переменных.
астным дифференциалом по х функции Z=f(x, y) называется главная часть частного приращения ΔxZ=f(x+Δx,y)-f(x,y), пропорциональная приращению Δx независимой переменной х. Аналогично определяется частный дифференциал по у, т.е. ΔyZ=f(y+Δy,x)-f(x,y).
Дифференциалы независимых переменных х и у просто равны их приращениям, т.е. dx=Δx, dy=Δy. Частные дифференциалы обозначаются так: dxZ -частный дифференциал по х, dyZ - частный дифференциал по у. При этом: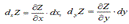 
Таким образом, частный дифференциал функции двух независимых переменных равен произведению соответствующей частной производной на дифференциал этой переменной.
Полный дифференциал функции двух переменных.
Полный дифференциал функции двух независимых переменных равен сумме произведений частных производных функции на дифференциалы соответствующих независимых переменных.
dZ=f'x(x,y)dx+f'y(x,y)dy или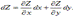 
Так как 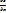dx=dxZ и 
dy=dyZ, то dZ=dxZ+dyZ, т.е. дифференциал функции двух независимых переменных равен сумме ее частных дифференциалов.
