этап. Решение задач разной степени сложности

Самостоятельное решение задач (предлагается 1-й уровень сложности).

Чему равен гравитационный центр треугольника с вершинами А(1;3), В(-1;-2), С(0;3)? (ответ (0; )).
Найдите а + в, если А (а;3), В (3;2), С(2;в) и Д (1;4). (ответ а + в=5).
Найдите расстояние от точки М (1;-2) до прямой 2х + у + 3=0. (ответ 0,6 ).

Решение задач в группах (предлагается 2-й уровень сложности).

Найдите точки пересечения окружности с центром в точке (3;4), радиусом равным 5 и прямой линией, заданной уравнением х + у - 8=0. (ответ (0;8), (7;1)).
Определите координаты центра тяжести треугольника с вершинами в точках М(-3;5), Р(13;-3) и К (5;-11). (ответ (5;-3).
Определить вид четырехугольника с вершинами в точках: А(6;7), В (8;2), с(4;3), Д(2;8).
Найдите расстояние от центра окружности до начала координат. (ответ 5).

Решение задач у доски (предлагается 3-й уровень сложности).

1. Составить уравнение прямой, содержащей медиану АК треугольника АВС с вершинами: А(1;3), В(5;-7), С (-1;9). (ответ у=-2х + 5).

2. Даны координат в точек Р(-1;5), Q (3;2). Найти координаты точки М, симметричной Р относительно точки Q. (ответ М(7;-1).

3. Определите косинус меньшего угла треугольника АВС, если известны координаты его вершин: А(-5;7), В(3;-1), С(-1;-9). (ответ ).

4. Окружность задана уравнением . Найдите координаты точек пересечения окружности с осью абсцисс. (ответ (2;0), (8;0)).

4 этап. Задание на дом. (индивидуальное).

Из сборников тестов найди и решить по 3 задачи

Уроки 31 - 32. Декартовы координаты.

Решение задач. Презентация задач.

Решение задач разной степени сложности.

Учащиеся предлагают задачи по теме из сборников тестов.

Уроки 33 -34. Зачет.

1 этап. (теоретические знания по пройденным темам)

2 этап. (решение 4 –х задач с пояснениями по индивидуальным карточкам).

3 этап. (решение 15 тестовых задач на 4 варианта из сборников тестов 2003-2010).

Дополнительный банк задач по теме «Треугольник. Четырехугольник».

Диагонали четырехугольника АВСД пересекаются в точке О. Найдите площадь четырехугольника АВСД, если площадь треугольников АВС, ВСД, АОД равны соответственно 34, 80, 168. (ответ 272)
Диагонали равнобедренной трапеции перпендикулярны, а отрезок, соединяющий середину меньшего основания и середину боковой стороны, равен 7. Найдите площадь трапеции.

(ответ 98).

Диагонали равнобедренной трапеции перпендикулярны, одно из оснований равно 17, а площадь равна 81. Найдите второе основание. (ответ 1)
Диагонали равнобедренной трапеции перпендикулярны и точкой пересечения делятся в отношении 3:4. Площадь четырехугольника с вершинами в серединах сторон трапеции равна 196. Найдите боковую сторону трапеции. (ответ 20)
Боковые стороны трапеции равны 12 и 16, а содержащие их прямые взаимно перпендикулярны, площадь трапеции равна 144. Найдите среднюю линию трапеции. (ответ 15)
В трапеции АВСД основания равны 13 и 26, одна из боковых сторон равна 5, а С - А = 90°. Найдите площадь трапеции. (ответ 90)
Найдите высоту трапеции, если ее диагонали взаимно перпендикулярны и равны 15 и 20.

(ответ 12)

Диагонали трапеции взаимно перпендикулярны, а средняя линия равна 13. Одна из диагоналей равна 10. Найдите другую диагональ. (ответ 24).
Диагональ равнобедренной трапеции перпендикулярна боковой стороне. Высота, проведенная из вершины тупого угла, делит основание на отрезки длиной 20 и 5. Найдите площадь трапеции. (ответ 200)
Диагонали трапеции АВСД с основанием ВС и АД пересекаются в точке О и равны 8 и 5. Найдите среднюю линию трапеции, если ВОС = 60°. (ответ 3,5)
Сторона параллелограмма равна 21, а диагонали равны 34 и 20. Найдите площадь параллелограмма. (ответ 336)
На стороне АВ параллелограмма АВСД отмечены точки К и М так, что АК = КМ = МВ. Отрезки СК и ДМ пересекаются в точке О. Площадь параллелограмма равна 40. Найдите площадь треугольника СОД. (ответ 15)
Найдите высоту ромба, если его меньшая диагональ равна 6, а сторона равна 5. (ответ 4,8)
Площадь ромба равна 600, а отношение длин диагоналей равно 4: 3. Найдите высоту ромба.

(ответ24).

Биссектрисы углов параллелограмма АВСД пересекают стороны ВС и АД в точках К и Р соответственно, причем ВС:КС= 5: 2. Площадь параллелограмма АВСД равна 75. Найдите площадь четырехугольника АКСР. (ответ 30)
В параллелограмме АВСД АВ=4, АД=8. Биссектрисы углов А и В пересекаются в точке К, углов С и Д – в точке М. Найдите КМ. (ответ 4)
Биссектрисы углов В и С параллелограмма АВСД пересекаются в точке К, лежащей на стороне АД. Площадь параллелограмма равна 36 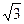, С=120°. Найдите большую сторону параллелограмма. (ответ 12).
Биссектриса угла А параллелограмма АВСД пересекает сторону ВС в точке К так, что ВК:КС= 4: 3. Найдите большую сторону параллелограмма, если его периметр равен 132. (ответ 42)
В треугольнике АВС А = 30°. На стороне АС взята точка К так, что АК =4, СК = 5, АВК = С. Найдите площадь треугольника ВКС. (ответ 7,5)
Медианы АК и ВМ треугольника АВС пересекаются в точке О, АВ=13, ВС=14, СА=15. Найдите площадь треугольника АОМ, (ответ 14)
Высоты АН и ВК равнобедренного треугольника АВС с основанием ВС пересекаются в точка О, АН = ВС = 8 . Найдите площадь треугольника АВО. (ответ 60)
Высоты АН и ВК равнобедренного треугольника АВС с основанием ВС пересекаются в точке О, АК=12, КС=8. Найдите АО. (ответ 6 ).
В прямоугольном треугольнике АВС на катете АС взята точка К так, что угол ВКС равен углу В. Найдите гипотенузу АВ, если СК=4,5 и АК= 3,5. (ответ 10)

Дополнительный банк задач по теме «Окружность и круг».

Хорда АВ делит окружность в отношении 11:7. Найдите в градусах меньший из вписанных углов, опирающихся на эту хорду. (ответ 70°).
В окружности радиуса 4 см проведен диаметр, и на нем взята точка А на расстоянии 3 см от центра. Найти радиус второй окружности, которая касается диаметра в точке А и изнутри касается данной окружности. (ответ 0,875).
Две одинаковые окружности расположены так, что каждая из них проходит через центр другой. Под каким углом в градусах видна общая хорда этих окружностей из центра одной из окружностей? (ответ 120°).
В окружности с центром в точке О хорды АВ и АС взаимно перпендикулярны. Угол СОА равен 54°. Найти угол АСВ. (ответ 63°).
Дан ромб со стороной 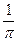и острым углом 60°. На его большей диагонали как на диаметре построена окружность. Найти площадь круга. (ответ 0,75).
Расстояние от центра О окружности до хорды СД равно 9см. Угол ОСД равен 45°. Точка К принадлежит хорде СД, причем СК = 3КД. Найти длину отрезка СК. (ответ 13,5).
Хорды МN и МК окружности равны по 18 см, а угол КМN равен 120°. Найдите диаметр этой окружности. (ответ 36).
Чему равна площадь сектора, образованного центральным углом окружности равного 60°, если длина окружности равна 12π. (ответ 6 π).
Площадь окружности равна 9 π. Чему равна длина дуги, лежащая напротив вписанного угла 60°. (ответ 2 π).
Стороны угла СЕД, равного 60°, касаются двух окружностей с центрами М и К, также касающихся одна другой, причем ЕМ = 21. Найдите радиус окружности с центром К (точка К расположена ближе к точке Е). (ответ 3,5).

Дополнительный банк задач по теме «Окружность, вписанная в треугольник и описанная около треугольника», «Окружность, вписанная в четырехугольник и описанная около четырехугольника».

В равнобедренном треугольнике основание равно 12, боковая сторона 10.Найти радиус описанной окружности. (ответ 6,25).
Радиус окружности, описанной около прямоугольного треугольника, равен 5, а радиус окружности, вписанной в этот треугольник, равен 2. найти периметр треугольника. (ответ 24).
Найти периметр ромба, зная, что длина его большей диагонали равна 10, а радиус вписанной окружности равен 3. (ответ 25).
Длина окружности 4π. Найти площадь квадрата, вписанного в эту окружность. (8).
Радиус вписанной в ромб окружности равен 5, а один из углов равен 60°. Найти длину большей диагонали ромба. (ответ 20).
Диаметр окружности, описанной около равностороннего треугольника, равен 48см. Найдите радиус окружности, вписанной в этот треугольник. (ответ 12).
Чему равна площадь описанной окружности, около равностороннего треугольника со стороной равной 2 см? (ответ ).
Трапеция СДЕК вписана в окружность (ДЕ II СК), ЕК = 5, КД = 12, причем КД перпендикулярно СД. Найдите длину окружности. (ответ13π).
Стороны треугольника 8см, 10см и 12см. Найти радиус описанной окружности. (ответ ).
Трапеция вписана в окружность (ВС II АД), АВ = 6, ВД = 8, ВД перпендикулярно АВ. Найти площадь круга, ограниченного этой окружностью. (ответ 25 π).
В четырехугольнике АВСД, описанном около окружности, АВ = 8, СД = 13, АД = 16. Найти сторону ВС. (ответ 5).
В прямоугольном треугольнике один из углов равен 30º. Найдите меньшую сторону треугольника, если радиус вписанной в него окружности равен 4см. (ответ 4 + 4 ).
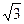Расстояния от центра вписанной в прямоугольную трапецию окружности до концов большей боковой стороны равны 6 и 8см. Найдите площадь трапеции. (ответ 94,08).
В прямоугольном треугольнике один из углов равен 60°, а расстояние от центра вписанной окружности до вершины этого угла равно 10см. Найдите большую сторону этого треугольника. (ответ 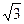10 +10).
Расстояние от центра вписанной в равнобедренную трапецию окружности до конца боковой стороны равны 9 и 12см. Найдите площадь трапеции. (ответ 216).
Найдите периметр прямоугольного треугольника, вписанного в окружность радиуса 13см, если один из катетов равен 10см. (ответ 60).
Найдите радиус окружности, описанной около треугольника со сторонами 10, 12 и 10см. (ответ 6,25).
Равнобедренная трапеция вписана в окружность так, что центр окружности принадлежит одному из оснований. Найдите углы трапеции, если один из углов между ее диагоналями равен 48°. (ответ 114°, 66°).
Каждая из боковых сторон и меньшее основание трапеции равны 5см, а один из ее углов равен 60°. Найдите радиус окружности, описанной около нее. (ответ 5).
Четырехугольник АВСД вписан в окружность так, что сторона АД является диаметром окружности, АВС = 121°, ВСД = 129°. Найдите углы ВАД, СДА, АСВ. (ответ 31°, 39°, 39°).

Дополнительный банк задач по теме «Векторы. Декартовы координаты».

Найти площадь квадрата со смежными вершинами в точках А(3; -7) и В(-1; 4).

(ответ 137).

Найти радиус окружности, проходящей через точки А(1; 1), В(1; -1), С(2; 0). (ответ 1).
Векторы и образуют угол в 120° и =3, =5. Найти (ответ 7).
Найти длину вектора , если А(-3; 2; -1), В(2; -1; -3), С(1; -4; 3), Д(-1; 2; -2). (ответ ).
Найти кратчайшее расстояние от точки В(3;9) до окружности - 26х +30у + 313 =0. (ответ 17).
Найти наибольшее значение m, при котором длины векторов (2 m; 2; 3) и (-6; -2; m) равны. (ответ 3).
Найти наибольший угол треугольника с вершинами в точках А(3; -1; 6), В(-1; 7; -2), С(1; -3; 2). (ответ ).
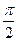Векторы , , 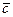попарно образуют друг с другом углы, каждый из которых равен 60°, =4, =2, =6. Найти . (ответ 10).
Найти сумму всех значений a, при которых вектор (a-3; 0,5) параллелен вектору (a-2; a-3). (ответ 6,5).
Найти угол между векторами 5 и -2 если (2; -3) и (-3; -2). (ответ ).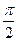
Через точку (1; 1) проходят две касательные к графику функции f(х) = 2 + 4х + 3. Найти сумму абсцисс точек касания. (ответ 2).
Найти косинус угла между векторами и 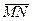, если С(3; -2; 1), Д(-1; 2; 1),

М(2; -3; 3), N(-1; 1; -2). (ответ 0,7).

Найти длину вектора - - 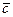, если = 2, =3, = 4, угол между и равен 60°, между и 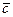равен 90° и между и 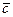равен 120°. (ответ ).
Найти угловой коэффициент прямой, проходящей через середину отрезка АВ перпендикулярно к АВ, если А(3; -6) и В(5; -4). (ответ -1).
К окружности, заданной уравнением -14у -95 = 0, проведена касательная, проходящая через точку М(0; -6). Найти расстояние от точки М до точки касания. (ответ 5).
Найти расстояние от прямой, заданной уравнением 4х + 3у = 12, до начала координат. (ответ 2,4).
Вычислите площадь треугольника, заключенного между осями координат и прямой, заданной уравнением -2х + 7у + 14 = 0. (ответ 7).
Даны вершины треугольника А(3; -4), В(-2; 3), С(5; 6). Найти квадрат длины медианы, проведенной из вершины В. (ответ 40).
Найти уравнение прямой, проходящей через точку А(-6; -6) и перпендикулярной к прямой у = - х + 2. (ответ: у = 3х + 12).
Диагонали выпуклого четырехугольника с вершинами в точках А(1; 1), В(6; 4),

С(6; 1), Д(1; -3) пересекаются в точке К. Найти отношение длин отрезков АК и КС. (ответ ).

Содержание:

Предисловие___________________________________________________________2

Треугольник___________________________________________________________ 3 - 4

Четырехугольники______________________________________________________ 5 - 9

Окружность и круг______________________________________________________10 - 11

Окружность, вписанная в треугольник и описанная около треугольника_________12 - 13

Окружность, вписанная в четырехугольник и описанная около четырехугольника_14 - 15

Векторы_______________________________________________________________16 - 17

Декартовы координаты__________________________________________________ 18 - 19

Дополнительный банк задач______________________________________________ 20 - 23

Литература.

К О Букубаев Геометрия 8 класс, А Шыныбеков геометрия 8, 9 классы (дополнительные главы).
Л С Атаносян и др. Геометрия. Дополнительные главы к школьному учебнику 9 класс. М «Просвещение» 1997г.
Учебно–методическое пособие и сборник тестов для поступающих в ВУЗы. И Акйол. Алматы 2006.
И П Рустюмова, С Т Рустюмова. Пособие для подготовки к ЕНТ по математике.
М И Сканави. Сборник задач по математике для поступающих в ВУЗы. М «Высшая школа» 1998г.
И Ф Шарыгин. 2200 задач по геометрии для школьников и поступающих в ВУЗы. Издательский дом «Дрофа» 1999г.
Научно – методический журнал «Математика и физика для школьников Казахстана.
Сборники тестов по математике. 2003-2010.
Г В Касаткина, Л В Шевченко. «Задачи и тесты по математике». «Дрофа» 2005.
Б Г Зив, В М Мейлер, А Г Баханский «Задачи по геометрии для 7-11 классов». М «Просвещение» 1991.