1 этап. Актуализация (задания из пройденного материала, необходимые для усвоения темы).
1. Треугольник вписанный в окружность и описанный около окружности.
2. Центр окружности, вписанной в треугольник. Центр окружности, описанной около треугольника.
2 этап. Дополнение к данной теме. (предлагается дополнительный материал, необходимый для быстрого решения задач по теме).
1. 
, где r- радиус вписанной в треугольник окружности, S- площадь треугольника, p- полупериметр.
2. 
, где S- площадь треугольника, R-радиус описанной окружности, а,в,с – стороны треугольника.
Этап. Решение задач разной степени сложности.
Самостоятельное решение задач (предлагается 1-й уровень сложности).
1. Катеты прямоугольного треугольника равны 6 и 8 см. чему равна площадь описанной окружности? (ответ 25 π см 
).
2. Чему равна площадь описанной окружности, около равностороннего треугольника со стороной равной 2 см? (ответ 
см ).
3. В прямоугольном треугольнике катет равен 7, а гипотенуза 25. Найдите радиус вписанной в треугольник окружности. (ответ 3).
Решение задач в группах (предлагается 2-й уровень сложности).
1. В правильный треугольник вписана окружность, радиус которой равен 5. Найдите медиану этого треугольника. (ответ 15).
2. Периметр правильного треугольника равен 42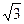 
см. Найдите длину окружности вписанной в него (ответ 14 π см)
3. В прямоугольный треугольник вписана окружность. Точка касания делит гипотенузу на отрезки, равные 2 и 3 см. найдите радиус этой окружности. (ответ 1).
4. Три окружности попарно касаются друг друга. Отрезки, соединяющие их центры, образуют прямоугольный треугольник. Найдите радиус меньшей окружности, если радиусы двух других равны 6 и 4. (ответ 2).
Решение задач у доски (предлагается 3-й уровень сложности).
1.В равнобедренном треугольнике высота 20, а основание относится к боковой стороне как 4:3. Найдите радиус вписанной окружности. (ответ8).
2. Треугольник вписан в окружность так, что одна из его сторон проходит через центр окружности, а две другие удалены от него на 6 см и 4 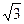см. Найдите площадь треугольника. (ответ 48 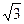см ).
3. Из одной точки окружности проведены две хорды длиной 10 и 12. Найдите радиус окружности, если расстояние от середины меньшей хорды до большей хорды равно 4. (ответ 
).
4. К окружности, вписанной в равнобедренный треугольник с основанием 12 и высотой 8, проведена касательная, параллельная основанию. Найдите длину отрезка данной касательной, заключенного между сторонами треугольника. (ответ 3).
4 этап. Задание на дом. (индивидуальное). Из сборников тестов найди и решить по 3 задачи.
Уроки 17-18. Окружность, вписанная в треугольник и описанная около треугольника.
