Задачі для підготовки до практичних занять:
19.1. Побудувати проекції лінії взаємного перетину поверхонь, використовуючи допоміжні січні площини (а), способи перетворення або допоміжне косокутне проекціювання.
62.
63.
64.
19.2. Побудувати лінію взаємного перетину заданих багатогранників.
65.
66.
Завдання 7. Взаємний перетин багатогранників
Умова: Побудувати лінію взаємного перетину заданих багатогранників. Показати видимість на площинах проекцій.
Завдання виконати на форматі А4. Варіанти наведені в табл. 7 збірника завдань.
Приклад виконання завдання наведено в методичних вказівках.
67.
Взаємний перетин кривих поверхонь
Задачі для підготовки до практичних занять:
20.1. Побудувати проекції лінії взаємного перетину заданих кривих поверхонь, використавши раціональний спосіб визначення лінії перетину.
68.
Аудиторні задачі:
20.2. Побудувати проекції лінії взаємного перетину заданих кривих поверхонь.
69.
70.
Завдання 8. Взаємний перетин кривих поверхонь
Умова: Побудувати лінію взаємного перетину двох заданих кривих поверхонь. Визначити видимість на проекціях.
Завдання виконати на аркуші формату А4. Варіанти наведені в табл. 8 збірника завдань.
Приклад виконання завдання наведено в методичних вказівках.
71.
Взаємний перетин граних та кривих поверхонь
Задачі для підготовки до практичних занять:
21.1. Побудувати лінію перетину двох заданих поверхонь.
72.
Аудиторні задачі:
21.2. Побудувати лінію перетину двох заданих поверхонь.
73.
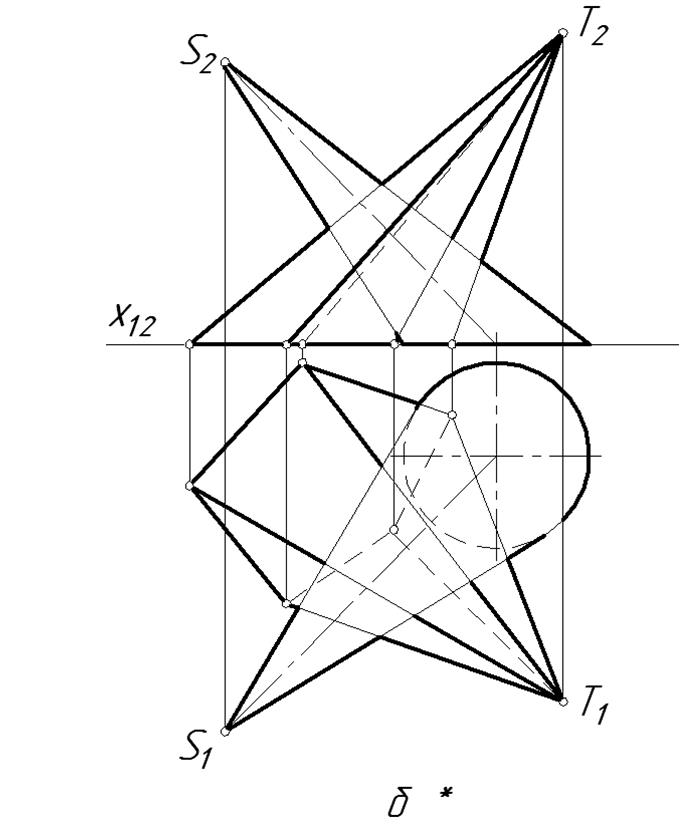
74.
Криві поверхні
Задачі для підготовки до практичних занять:
22.1. Побудувати горизонтальну 22.2. Побудувати проекції косої
проекцію точки А, яка належить площини, якщо задані проекції
конічній поверхні. Конічна поверхня двох її прямолінійних
обертання визначена твірною а, віссю i напрямних m і n, а площина
та вершиною S. паралелізму паралельна площині проекції П2.
22.3. Побудувати переріз поверхні 22.4. Побудувати фронтальну
обертання, заданої головним проекцію гвинтової поверхні,
меридіаном а і віссю i, горизонтально утвореної трикутним профілем.
проекціювальною площиною Σ. Побудувати горизонтальну проекцію перерізу цієї поверхні площиною Σ.
75.
22.5. Побудувати проекції 22.6. Побудувати проекції
кільцевого коноїда. прямого гелікоїда.
22.7. Побудувати проекції циліндроїда 22.8. Побудувати проекції
загального виду. коноїда загального виду.
Завдання 9. Утворення і зображення кривих поверхонь
Умова. 1. Побудувати проекції однієї поли розгортного гелікоїда за заданою гвинтовою лінією (М1:1).
2. Побудувати проекції розгортного кільцевого гелікоїда за заданими: діаметром горизонтальної проекції гвинтової лінії, діаметром основи січного співвісного циліндра і кроком (М1:1).
76.
3. Побудувати проекції поверхні з ребром звороту за заданими проекціями ребра звороту т та перерізати її вертикальною площиною σ.
4. Побудувати поверхню однакового схилу за заданим кутом схилу 
і проекціями лінії бровки. Знайти ребро звороту.
5. Побудувати проекції схилів насипу ділянки полотна дороги з кутом схилу 45°.
6. Побудувати проекції косої площини за напрямними а і b та площиною паралелізму твірних ω. Знайти точки зустрічі прямої d з косою площиною.
7. Побудувати косу площину за заданими напрямними а і b та фронтально проекціювальною площиною паралелізму ω. Знайти переріз її трикутним фронтально проекціювальним відсіком δ. Визначити видимість частин відсіку.
8. Побудувати проекції циліндроїда за заданими кривими напрямними m і n та горизонтально проекціювальною площиною паралелізму ω. Знайти лінію перерізу поверхні циліндроїда трикутним горизонтально проекціювальним відсіком σ.
9. Побудувати проекції циліндроїда, напрямними якого є криві m і n, а площина паралелізму – горизонтальна. Перерізати поверхню циліндроїда горизонтально проекціювальною площиною σ.
10. За заданими напрямними – прямою а та кривою m, побудувати проекції коноїда. Площина паралелізму фронтальна. Перерізати поверхню коноїда фронтально проекціювальним відсіком σ.
11. Побудувати проекції однієї поли розгортного гелікоїда, у якого напрямною є циліндрична гвинтова лінія з кроком 100 мм і діаметром горизонтальної проекції гвинтової лінії 70 мм. Перерізати гелікоїд фронтально проекціювальною площиною μ, яка проходить через вісь гвинтової лінії (М1:1).
12. Побудувати проекції витка пружини квадратного перерізу 12x12 мм. Крок витка 90 мм (М1:1).
13. Побудувати проекції витка трапецоїдної різьби. Крок витка 85 мм. Висота трапеції 12 мм. Паралельні сторони 8 і 12 мм (М1:1).
14. Побудувати проекції гвинтової трикутної різьби на циліндрі з діаметром основи 70 мм. Профіль різьби – рівносторонній трикутник, крок – 54 мм (М1:1).
15. Побудувати проекції гвинтового коноїда, твірна якого горизонтальна. Один кінець твірної ковзає по напрямній – циліндричній гвинтовій лінії, діаметр горизонтальної проекції якої – 42 мм, крок – 42 мм. Другий кінець твірної переміщується по вертикальній прямій а. Перерізати поверхню гвинтового коноїда горизонтально проекціювальною площиною.
16. Відрізок а обертається навколо вісі S. Побудувати проекції однопорожнинного гіперболоїда обертання.
17. Побудувати проекції розгортного гелікоїда з глибинною віссю S (М1:1).
18. Побудувати проекції гелікоїдального циліндра (гвинтової трубчатої поверхні), утвореного рухом кулі (діаметром 10 мм), центр якого послідовно переміщується по заданій гвинтовій лінії з кроком 80 мм і діаметром горизонтальної проекції 60 мм (М1:1).
77.
19. Побудувати проекції коноїда, напрямними якого є вертикальна пряма а і фронтальне півколо m. Твірні – горизонтальні. Перерізати коноїд фронтально проекціювальною площиною μ.
20. Побудувати проекції косого кільцевого гелікоїда за напрямними: циліндричною лінією, конусом і співвісними з ними циліндрами діаметрами 56 і 28 мм.
21. Побудувати проекції однопорожнинного гіперболоїда обертання за твірною 
, віссю s, верхньою і нижньою основами. Перерізати поверхню гіперболоїда фронтально проекціювальною площиною.
22. Побудувати проекції однієї поли розгортного гелікоїда, у якого напрямною є циліндрична гвинтова лінія з кроком 80 мм та діаметром горизонтальної проекції гвинтової лінії 50 мм (М1:1).
23. Побудувати проекції гвинтового циліндроїда за напрямними: гвинтовою лінією і циліндром (М1:1). Перерізати поверхню фронтально проекціювальною площиною μ.
24. Побудувати проекції косого кільцевого гелікоїда за напрямними: циліндричною гвинтовою лінією, конусом і співвісними з ними циліндрами діаметрами 56 і 28 мм.
25. Побудувати проекції коноїда по заданим напрямним: вертикальною прямою а і фронтальним колом m. Площина паралелізму горизонтальна. Задати горизонтальну проекцію точки, яка лежить на поверхні коноїда, та знайти її фронтальну проекцію.
26. Побудувати проекції косої площини за заданими напрямними і 
та горизонтальною площиною паралелізму. Знайти лінію перерізу косої площини трикутним відсіком α.
27. Побудувати проекції циліндроїда за заданими напрямними m і n та фронтальною площиною паралелізму. Знайти лінію перерізу трикутним відсіком α.
28. Побудувати проекції кривого циліндра (трубчатої поверхні), утвореного рухом кулі, центр якої переміщується по кривій т. Діаметр кулі – 20 мм.
29. Побудувати проекції розгортного гелікоїда з глибинною віссю S.
30. Побудувати проекції косого циліндра з трьома напрямними: заданою гвинтовою лінією, її віссю та напрямним конусом обертання.
Завдання виконати на аркуші формату А4. Варіанти наведені в табл. 9 збірника завдань.
Приклад виконання завдання наведено в методичних вказівках.
78.
Дотичні площини
Задачі для підготовки до практичних занять:
23.1. Побудувати сліди площини 23.2. Побудувати проекції площини,
дотичної до поверхні конуса, яка яка дотична до конуса і паралельна
проходить через зовнішню точку А. прямій n.
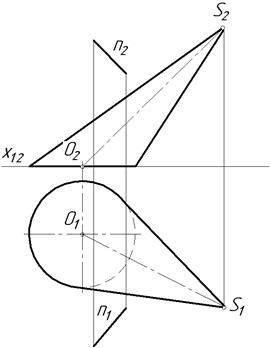
23.3. Побудувати проекції 23.4. Побудувати проекції площини
площини дотичної до дотичної до циліндра, яка проходить
поверхні тора в точці А. 
через зовнішню точку А.
79.
Аудиторні задачі:
23.5. Побудувати сліди площини 23.6. Побудувати сліди площини
дотичної до поверхні циліндра і дотичної до поверхні сфери в точці А,
паралельної прямій а. яка належить поверхні сфери.
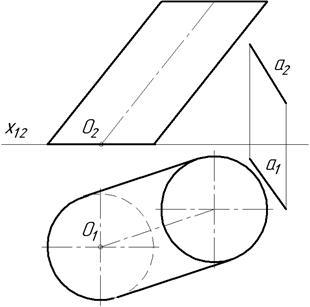
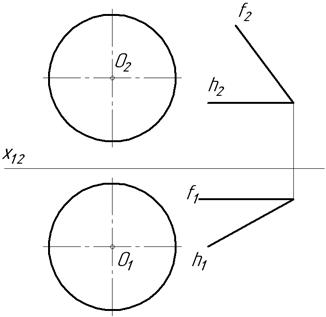
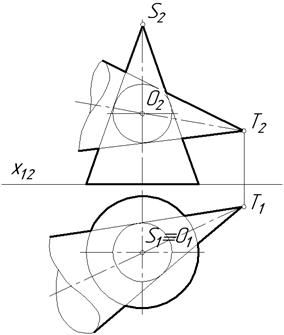
23.7. Побудувати площину дотичну 23.8. Побудувати сліди площини
до сфери, яка паралельна заданій дотичної до двох конусів, які площині f,h. описані навколо кулі.
80.
Завдання 10. Дотичні площини
Умова: Провести до кривих поверхонь дотичні площини, які проходять: через точку А, яка лежить на поверхні (варіанти 1–6); через точку А, що не належить поверхні (варіанти 7–12); паралельно заданій прямій (варіанти 13–18); через пряму, що не належить поверхні (вар. 19–24); паралельно заданій площині (вар. 25-30).
Завдання виконати на аркуші формату А4. Варіанти наведені в табл. 10 збірника завдань.
Приклад виконання завдання наведено в методичних вказівках.
Аксонометричні проекції
Задачі для підготовки до практичних занять:
24.1. Побудувати прямокутну ізометрію призми з призматичним наскрізним отвором.
81.
24.2. Побудувати прямокутну діметрію призми з наскрізним призматичним отвором.
Аудиторні задачі:
24.3. Побудувати фронтальну ізометрію заданої фігури.
82.
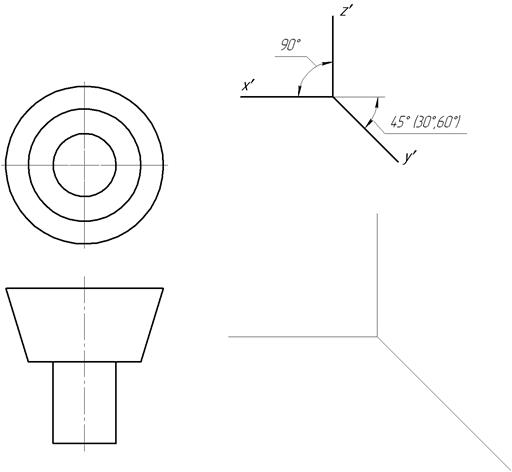
24.4. Побудувати горизонтальну ізометрію заданої фігури.
24.5. Побудувати фронтальну діметрію заданої фігури.
83.
Програмований контроль
Тема №1: Точка № варіанту _______ Дата _______
| Запитання | ||||||||||
| Відповіді |
Оцінка _____________________
Тема №2: Пряма № варіанту ______ Дата _______
| Запитання | ||||||||||
| Відповіді |
Оцінка _____________________
Тема №3: Площина № варіанту ______ Дата ______
| Запитання | ||||||||||
| Відповіді |
Оцінка _____________________
Тема №4: Перетин прямих і № варіанту ______ Дата ______ площин
| Запитання | ||||||||||
| Відповіді |
Оцінка _____________________
Тема №5: Паралельність та перпендику- № варіанту ______ Дата _______
лярність прямої і площини
| Запитання | ||||||||||
| Відповіді |
Оцінка _____________________
84.
Тема №6: Дві площини № варіанту______ Дата________
| Запитання | ||||||||||
| Відповіді |
Оцінка _____________________
Тема №7: Багатогранники і № варіанту ______ Дата ______
криві поверхні
| Запитання | ||||||||||
| Відповіді |
Оцінка _____________________
Тема №8: Плоско-паралельне № варіанту ______ Дата ______
переміщення
| Запитання | ||||||||||
| Відповіді |
Оцінка _____________________
Тема №9: Перетин багатогранників № варіанту ______ Дата ______
прямою лінією
| Запитання | ||||||||||
| Відповіді |
Оцінка _____________________
85.
Студенту бажано користуватись запропонованими підручниками:
1. Браїловський В.В. та ін. Інженерна та комп’ютерна графіка. –Чернівці: Рута, 2008. – 320 с.
2. Бубенников А.В., Громов М.Я. Начертательная геометрия. – 3-е изд. – М.: Высшая школа, 1985. – 416 с.
3. Гордон В.О., Семенцов-Огиевский М.А. Курс начертательной геометрии. – М.: Наука, 1988. – 272 с.
4. Иванов Г.С. Начертательная геометрия.– М.: Машиностроение, 1995. – 310 с.
5. Колотов С.М и др. Курс начертательной геометрии. – К.: Госстройиздат УССР, 1961.– 264 с.
6. Кущ М.В., Князєв В.І. Нарисна геометрія в лекціях. Навчальний посібник. – К.: КНУТД, 2007. – 112 с.
7. Кущ М.В., Ковальов Ю.А., Князєв В.І. та ін. Нарисна геометрія: Навчальний посібник. – К.: КНУТД, 2010. – 259 с.
8. Михайленко В.Е. і др. Інженерна та комп’ютерна графіка. – К.: Вища школа, 2006. – 342 с.
9. В.Є. Михайленко – Збірник задач з інженерної та комп’ютерної графіки. Київ. Вища школа, 2003. – 270 с.
86.
