Загальні положення
Пряма паралельна площині, якщо вона паралельна одній з прямих цієї площини.
Дві площини паралельні, якщо дві прямі які перетинаються однієї площини відповідно паралельні до двох прямі які перетинаються другої площини.
Дві площини, які задані слідами, паралельні, якщо однойменні сліди площин паралельні між собою.
Головні лінії (горизонталі і фронталі) двох паралельних прямих паралельні.
Задачі для підготовки до практичних занять:
 8.1. Провести через точку А пряму паралельну заданій площині.
8.1. Провести через точку А пряму паралельну заданій площині.
а б
8.2. Чи паралельний відрізок АВ заданій площині?

а б
24.
8.3. Провести через точку К площину паралельну заданій площині.
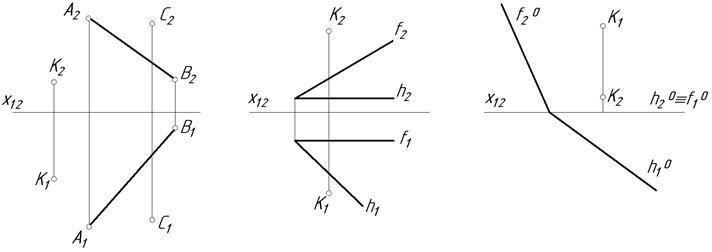
а б в
Аудиторні задачі:
8.4. Через точку С провести пряму, яка перетинала б відрізок АВ і залишалась паралельною заданій площині.

а б в
25.
Перпендикулярність прямої та площини.
Перпендикулярність площин
Загальні положення
1. Пряма перпендикулярна до площини, якщо вона перпендикулярна до двох непаралельних прямих цієї площини.
Прямий кут проекціюється в натуральну величину якщо одна з його сторін паралельна до площини проекцій (див. 10). Враховуючи цю теорему про властивість прямого кута, доцільно за дві непаралельні прямі взяти горизонталь і фронталь площини. Тоді пряма перпендикулярна до площини, якщо її горизонтальна проекція перпендикулярна горизонтальній проекції горизонталі, а фронтальна проекція перпендикулярна до фронтальної проекції фронталі.

Рис. 10
Якщо площина задана слідами, то пряма перпендикулярна площині коли проекції прямої перпендикулярні відповідним слідам.
2. Площини взаємно перпендикулярні, якщо одна з площин проходить через пряму яка перпендикулярна до другої площини.
26.
Задачі для підготовки до практичних занять:
9.1. Побудувати з точки К перпендикуляр довжиною 20 мм до заданої площини.

а <<*>> б
9.2. Опустити перпендикуляр з точки К на задану площину. Визначити відстань від точки К до площини АВС.

а б в
27.
Аудиторні задачі:
9.3. Через пряму MN провести площину перпендикулярну до заданої.

а

б
28.
Перетин площин
Загальні положення
1. Дві площини перетинаються по прямій лінії (див. рис. 11). Для побудови лінії перетину двох площин, треба знайти дві точки спільні для цих площин.

Рис. 11
Довільну точку,яка належить лінії взаємного перетину двох площин. Визначають як точку перетину довільної прямої однієї з площин з другою площиною (див. § 7), або з використання допоміжної січної площини:
а) будують довільну січну площину, яка перетинає ці площини;
б) визначають лінії перетину заданих площин допоміжною;
в) на перетині визначених ліній знаходять точку, яка належить лінії взаємного перетину двох площин.
2. Якщо задані площини визначені слідами, то точки перетину однойменних слідів визначають їхню лінію перетину.
Задачі для підготовки до практичних занять:
10.1. Побудувати лінію перетину площин. Визначити видимість.

а б
29.
Аудиторні задачі:
10.2. Побудувати лінію перетину площин. Визначити видимість.

а б
Завдання 2. Площина. Взаємно перпендикулярні та паралельні площини
Умова: а) Визначити натуральну величину відстані від точки D до площини заданої трикутним відсіком АВС; б) побудувати площинку яка паралельна площині DEK та віддалена від неї на 35 мм; в)через пряму DK провести площину яка перпендикулярна до заданої площини АВС. Побудувати лінію їх взаємного перетину та визначити видимість елементів площин в проекціях. Позначити проекції кута між прямою DK та площиною АВС.
Завдання виконати на 3 аркушах формату А4 в масштабі 1:1. Координати точок по варіантах наведені в табл. 2 збірника завдань.
Приклад виконання завдання наведено в методичних вказівках.
30.






