На электрических схемах двухобмоточный трансформатор представляется следующим образом (рис. 5.1):
В обмотках указывается схемы соединения обмоток (звезда, звезда с нулем, треугольник) и режим работы нейтрали:
· звезда – с изолированной нейт- ралью;
· звезда с нулем – имеется соеди-нение нейтрали с землей.
В соответствии с принятой систе-мой обозначений аббревиатура транс-форматора ТДН-10000/110/10 расшиф-ровывается: трансформатор трехфазный, двухобмоточный с принудительной циркуляцией воздуха и естественной циркуляцией масла и системой регулирования напряжения под нагрузкой. Номинальная мощность – 10000 кВ∙А, класс напряжения обмотки высшего напряжения – 110 кВ, низшего напряжения – 10 кВ.
В практических расчетах двухобмоточный трансформатор чаще всего представляется Г-образной схемой замещения (рис. 5.2).
Активное и реактив-ное сопротивления трас-форматора (продольная ветвь) представляют собой сумму активных и реак-тивных сопротивлений об-мотки высшего напряже-ния и приведенной к ней обмотки низшего напря-жения:
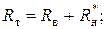
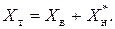
Поперечная ветвь схемы замещения представлена активной G т и реактивной В т проводимостями. Проводимости обычно подключают со стороны первичной обмотки: для повышающих трансформаторов – со стороны обмотки низшего напряжения, для понижающих – со стороны обмотки высшего напряжения.
В такой схеме замещения отсутствует трансформация, то есть отсутствует идеальный трансформатор. Поэтому в расчетах вторичное напряжение 
оказывается приведенным к напряжению первичной обмотки.
Активная проводимость обусловлена потерями активной мощности в стали трансформатора на перемагничивание и вихревые токи, реактивная проводимость – намагничивающей мощностью. В расчетах режимов электрической сети проводимости заменяются нагрузкой, равной потерям холостого хода.
Параметры схемы замещения трансформатора определяются из двух опытов – холостого хода и короткого замыкания. В опытах определяют следующие величины, которые указывают в паспортных данных трансформатора:
· потери активной мощности в режиме холостого хода 
в кВт;
· потери активной мощности в режиме короткого замыкания 
в кВт;
· напряжение короткого замыкания U к, в %;
· ток холостого хода I х, в %.
Величины активного и реактивного сопротивлений находят из опыта короткого замыкания (рис. 5.3). Опыт выполняют следующим образом: обмотку низшего напряжения закорачивают, а на обмотку высшего напряжения подают такое напряжение (U к), чтобы в обеих протекал номинальный ток.
Так как напряжение короткого замыкания намного меньше номинального напряжения трансформатора, то потери активной мощности в проводимости практически равны нулю. Таким образом, все потери активной мощности в режиме короткого замыкания идут на нагрев обмоток. Математически это можно записать:
(5.1)
Если в формуле (5.1) значение тока записать через мощность и номинальное напряжение обмотки высшего напряжения
,
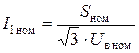то получим выражение для расчета активного сопротивления двухобмоточного трансформатора:
Напряжение короткого замыкания U к складывается из падения напряжения на активном U к а и реактивном U к р сопротивлениях. Выразим их в процентах от номинального напряжения.
Падение напряжения в активном сопротивлении трансформатора:
Подставим в выражение значение R т. Получим:
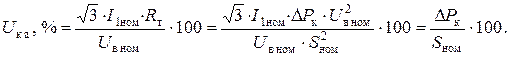
Таким образом, величина падения напряжения в активном сопротивлении, выраженная в процентах, пропорциональна потерям активной мощности в режиме короткого замыкания.
Выражение для падения напряжения в реактивном сопротивлении в процентах выглядит следующим образом
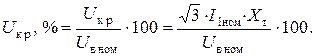(5.2)
Из него можем найти величину реактивного сопротивления трансформатора:
Умножим и разделим полученное выражение на U в ном:
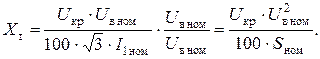
В современных трансформаторах активное сопротивление гораздо больше реактивного. Поэтому в практических расчетах можно принять, что U к р ≈ U к. Тогда, формула для расчета индуктивного сопротивления трансформатора имеет вид:
Трансформаторы имеют устройства регулирования напряжения (РПН или ПБВ), которые позволяют менять коэффициенты трансформации. Поэтому величина U к (следовательно, и величина индуктивного сопротивления) зависит от ответвления устройств РПН или ПБВ. В расчетах установившихся режимов этой зависимостью пренебрегают. Ее учитывают при расчете токов короткого замыкания при выборе устройств автоматики и релейной защиты.
Проводимости ветви намагничивания определяются из опыта холостого хода (рис. 5.4), который выполняется при номинальном напряжении. В этом режиме трансформатор потребляет мощность, равную потерям холостого хода:
.
Потери активной мощности пропорциональны активной проводимости трансфор
Отсюда может быть определена величина активной проводимости:
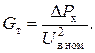
Потери реактивной мощности пропорциональны реактивной проводимости трансформатора:
Следовательно, величина реактивной проводимости трансформатора равна:
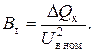
Величина потерь реактивной мощности пропорциональна току намагничивания
(5.3)
где U ном ф – фазное номинальное напряжение трансформатора.
Величина тока холостого хода складывается из тока намагничивания I μ и тока в стали I стали:
I х = I μ + I стали.
Так как величина тока в стали составляет около 10 % от тока намагничивания, то выражение (5.3) можно записать:
В паспортных данных величина тока холостого хода приводится в процентах от номинального тока. Поэтому мы можем записать:
С учетом полученного выражения, формула для расчета реактивной проводимости имеет вид:
