При повышении напряжения слой изоляции нужно увеличивать. Это не выгодно. Поэтому при напряжении 35 кВ и выше кабели выполняются с отдельно освинцованными или экранированными жилами. И электрическое, и тепловое поля – радиальные (рис. 3.5 б).
Кабели с вязкой пропиткой имеют существенный недостаток: после снятия токовой нагрузки, т.е. при остывании в кабеле появляются газовые включения. Это связано с тем, что коэффициент линейного расширения кабельной массы значительно больше коэффициента линейного расширения изолирующей бумаги. Диэлектрическая прочность газовых включений меньше в несколько раз, чем у бумаги. При повышении напряженности электрического поля это может привести к пробою изоляции.
Чтобы избежать этого при напряжениях 10 – 110 кВ применяют газонаполненные кабели. Это освинцованные кабели. Фазная изоляция выполняется из обедненно-пропитанной бумаги. Кабель находится под небольшим избыточным давлением (0,1 – 0,3 МПа) инертного газа (азота). Это повышает изолирующие свойства бумаги. Постоянство давления обеспечивается непрерывной подпиткой газа.
При напряжении 110 – 500 кВ используются маслонаполненные кабели. Жилые выполняют полыми и заполняют их маловязким очищенным маслом под давлением до 1,6 МПа. Избыточное давление исключает возможность образования пустот в изоляции кабеля, что увеличивает его электрическую прочность. В зависимости от величины давления различают маслонаполненные кабели высокого и низкого давления. Маслопроводящий канал через специальные муфты на трассе соединяется с баками давления.
Маркируются кабели по начальным буквам элементов, которые характеризуют их конструкцию:
· жила – буква А для алюминия, без обозначения для меди;
· оболочка – буква А для алюминия, С – для свинца, В – для поливинилхлорида, Н – для резины, П – для полиэтилена;
· броня – буква Б для стальных лент, П – для плоских освинцованных проволок, К – для круглых освинцованных проволок, Г – для кабелей без брони и защитного слоя.
Если кабели выполняются с отдельно освинцованными жилами, то в маркировке указывается буква О.
Для маслонаполненных кабелей низкого давления перед основной аббревиатурой указывают буквы МН, а для кабелей высокого давления – МВД.
После аббревиатуры указывают количество жил и сечение жил в мм2.
Например, ААБ-3 х 120 – трехжильный алюминиевый кабель с алюминиевой оболочкой и броней из свинца с сечением жил 120 мм2; СБ-3 х 95 трехжильный медный кабель со свинцовыми оболочкой и броней сечением жил 95 мм2.
Лекция № 4
Схемы замещения и параметры элементов электрических сетей
План.
8. Активное сопротивление.
9. Реактивное сопротивление.
10. Активная проводимость.
11. Реактивная проводимость.
12. Схема замещения ЛЭП.
В состав электрической сети входят различные по назначению и конструкции элементы (ЛЭП, трансформаторы и т.д.). Но на каждом из участков её можно охарактеризовать одинаковым набором параметров, отражающих свойства элементов и различающихся между собой только количественно.
Каждый элемент электрической сети представляется в виде схемы замещения. Расчётная схема электрической сети, таким образом, образуются в результате объединения схем замещения отдельных элементов с учётом последовательности соединения их в сеть.
Любая ЛЭП, строго говоря, обладает большим количеством равномерно распределённых вдоль неё бесконечно малых активных и реактивных сопротивлений и проводимостей. Точный их учёт необходим при расчёте длинных линий (ВЛЭП больше 300 км, для КЛЭП больше 50 км). В практических расчётах ограничиваются упрощёнными методами и считают, что ЛЭП обладает не распределёнными, а сосредоточенными сопротивлениями и проводимостями.
Активное сопротивление
Активное сопротивление зависит от материала, сечения и температуры. Активное сопротивление обусловливает тепловые потери проводов и кабелей. Определяется материалом токоведущих проводников и площадью их сечения.
Различают сопротивление проводника постоянному току (омическое) и переменному току (активное). Активное сопротивление больше активного (R а > R ом) из-за поверхностного эффекта. Переменное магнитное поле внутри проводника вызывает противоэлектродвижущую силу, благодаря которой происходит перераспределение тока по сечению проводника. Ток из центральной его части вытесняется к поверхности. Таким образом, ток в центральной части провода меньше, чем у поверхности, то есть сопротивление провода возрастает по сравнению с омическим. Поверхностный эффект резко проявляется при токах высокой частоты, а также в стальных проводах (из-за высокой магнитной проницаемости стали).
Для ЛЭП, выполненных из цветного металла, поверхностный эффект на промышленных частотах незначителен. Следовательно, R а ≈ R ом.
Обычно влиянием колебания температуры на R а проводника в расчётах пренебрегают. Исключение составляют тепловые расчеты проводников. Пересчет величины сопротивления выполняют по формуле:
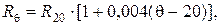
где R 20 – активное сопротивление при температуре 20о;
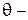текущее значение температуры.
Активное сопротивление зависит от материала проводника и сечения:
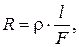
где ρ –удельное сопротивление, Ом мм2/км;
l – длина проводника, км;
F – сечение проводника, мм2.
Сопротивление одного километра проводника называют погонным сопротивлением:
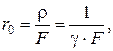
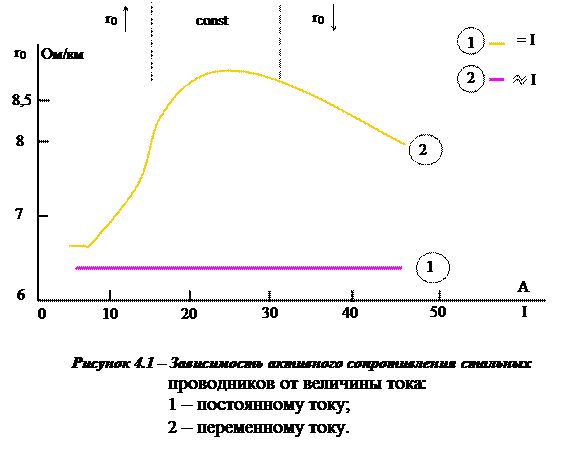
где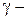 
удельная проводимость материала проводника, км См/мм2.
Для меди γCu=53×10-3 км См/мм2, для алюминия γAl=31.7×10-3 км См/мм2.
На практике значение r 0 определяют по соответствующим таблицам, где они указаны для t0=200С.
Величина активного сопротивления участка сети рассчитывается:
R = r 0× l.
Активное сопротивление стальных проводов намного больше омического из-за поверхностного эффекта и наличия дополнительных потерь на гистерезис (перемагничивание) и от вихревых токов в стали:
r 0 = r 0пост + r 0доп,
где r 0пост – омическое сопротивление одного километра провода;
r 0доп – активное сопротивление, которое определяется переменным магнитным полем внутри проводника, r 0доп = r 0поверх.эф + r 0гистер. + r 0вихр.
Изменение активного сопротивления стальных проводников показано на рисунке 4.1.
При малых величинах тока индукция прямо пропорциональна току. Следовательно, r 0 увеличивается. Затем наступает магнитное насыщение: индукция и r 0 практически не изменяются. При дальнейшем увеличении тока r 0 уменьшается из-за снижения магнитной проницаемости стали (m).
 |
Зависимость r 0= f (F) имеет вид (см. рис. 4.2):
Из рис. 4.2 видно, что при малых значениях сечения r 0 имеет большое значение. При увеличении сечения величина r 0 уменьшается.
Индуктивное сопротивление
Переменный ток, проходя по проводу, образует вокруг него переменное магнитное поле, которое наводит в проводнике ЭДС обратного направления (ЭДС самоиндукции). Сопротивление току, обусловленное противодействием ЭДС самоиндукции, называется реактивным индуктивным сопротивлением.
Величина реактивного индуктивного сопротивления зависит как от значения тока в собственном проводе, так и от величины токов в соседних проводах. Чем дальше расположены фазные провода линии, тем меньше влияние соседних проводов – поток рассеяния и индуктивное сопротивление увеличиваются.
На величину индуктивного сопротивления оказывает влияние диаметр провода, магнитная проницаемость (m) и частота переменного тока. Величина погонного индуктивного сопротивления рассчитывается по формуле:
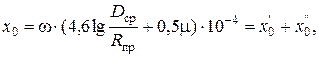(4.1)
где w – угловая частота;
m – магнитная проницаемость;
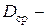среднегеометрическое расстояние между фазами ЛЭП;
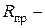радиус провода.
Погонное индуктивное сопротивление состоит из двух составляющих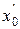 
и 
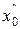. Величина 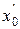называется внешним индуктивным сопротивлением. Обусловлено внешним магнитным полем и зависит только от геометрических размеров ЛЭП. Величина 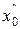называется внутренним индуктивным сопротивлением. Обусловлено внутренним магнитным полем и зависит только от m, то есть от тока проходящего по проводнику.
Среднегеометрическое расстояние между фазными проводами рассчитывается по формуле:
.
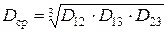На рис. 1.3 показано возможное расположение проводов на опоре.
При расположении проводов в одной плоскости (рис. 4.3 а, б) формула для расчета D ср упрощается:
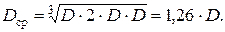
Если же провода расположены в вершинах равностороннего треугольника, то D ср = D .
Для ВЛЭП напряжением 6-10 кВ расстояние между проводами составляет 1-1,5 м; напряжением 35 кВ – 2-4 м; напряжением 110 кВ – 4-7 м; напряжением 220 кВ – 7-9м.
 |
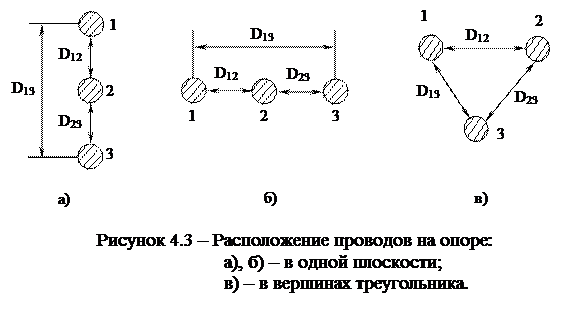При f = 50Гц значение w =2×p× f = 3,14 1/с. Тогда формула (4.1) записывается следующим образом:
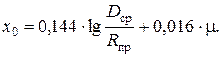
Для проводников выполненных из цветного металла (медь, алюминий) m = 1.
На ЛЭП высокого напряжения (330 кВ и выше) применяют расщепление фазы на несколько проводов. На напряжении 330 кВ обычно используют 2 провода в фазе (индуктивное сопротивление снижается приблизительно на 19%). На напряжении 500 кВ обычно используют 3 провода в фазе (индуктивное сопротивление снижается приблизительно на 28%). На напряжении 750 кВ используют 4-6 проводов в фазе (индуктивное сопротивление снижается приблизительно на 33%).
Величина погонного индуктивного сопротивления при расщепленной конструкции фазы рассчитывается как:
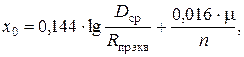
где n – количество проводов в фазе;
R пр экв – эквивалентный радиус провода.
При n = 2, 3
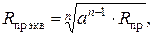
где а – шаг расщепления (среднегеометрическое расстояние между проводами в фазе);
R пр – радиус провода.
При большем количестве проводов в фазе их располагают по окружности (см. рис. 4.4). В этом случае величина эквивалентного радиуса провода равна:
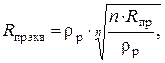
где r p – радиус расщепления.
Величина погонного индуктивного сопротивления зависит от радиуса провода, и практически не зависит от сечения (рис. 4.5).
Величина x 0 уменьшается при увеличении радиуса провода. Чем меньше средний диаметр провода, тем больше x 0, так как в меньшей степени влияют соседние провода, уменьшается ЭДС самоиндукции. Влияние второй цепи для двухцепных ЛЭП проявляется мало, поэтому им пренебрегают.
Индуктивное сопротивление кабеля намного меньше чем у воздушных ЛЭП из-за меньших расстояний между фазами. В ряде случаев им можно пренебречь. Сравним погонное индуктивное кабельных и воздушных линий разных напряжений:
| Номинальное напряжение, кВ | КЛЭП | ВЛЭП |
| 0,06 | 0,31 | |
| 0,125 | 0,4 |
Величина реактивного сопротивления участка сети рассчитывается:
Х = х 0× l.
Активная проводимость
Активная проводимость (G) обусловлена потерями активной мощности в диэлектриках. Ее величина зависит от:
· тока утечки по изоляторам (малы, можно пренебречь);
· потерь мощности на корону.
Активная проводимость приводит к потерям активной мощности в режиме холостого хода ВЛЭП. Потери мощности на корону (D R кор) обусловлены ионизацией воздуха вокруг проводов. Когда напряжённость электрического поля у провода становится больше электрической прочности воздуха (21,2кВ/см), на поверхности провода образуются электрические разряды. Из-за неровностей поверхности многопроволочных проводов, загрязнений и заусениц разряды появляются вначале только в отдельных точках провода – местная корона. По мере повышения напряжённости корона распространяется на большую поверхность провода и в конечном счёте охватывает провод целиком по всей длине – общая корона.
Потери мощности на корону зависят от погодных условий. Наибольшие потери мощности на корону происходят при различных атмосферных осадках. Например, на воздушных ЛЭП напряжением 330¸750кВ DRкор при снеге повышаются на 14%, дожде – на 47%, изморози – на 107% по сравнению с потерями при хорошей погоде. Корона вызывает коррозию проводов, создаёт помехи на линиях связи и радиопомехи.
Величину потерь мощности на корону можно рассчитать по формуле:
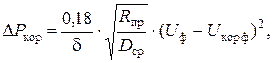кВт/км
где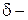 
коэффициент, учитывающий барометрическое давление;
U ф, U кор ф – соответственно фазные рабочее напряжение ЛЭП и напряжение, при котором возникает корона.
Начальная напряжённость (в хорошую погоду), при которой возникает общая корона рассчитывается по формуле Пика:
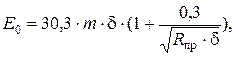кВ/см
где m – коэффициент негладкости привода;
R пр – радиус провода, см;
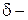коэффициент, учитывающий барометрическое давление.
Для гладких цилиндрических проводов значение m = 1, для многопроволочных проводов – m = 0,82¸0,92.
Величина δ рассчитывается по формуле:
,
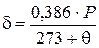где Р – давление, мм ртутного столба;
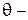температура воздуха, 0C.
При нормальном атмосферном давлении (760 мм рт. ст.) и температуре 20 0C d = 1. Для районов с умеренным климатом среднегодовое значение d равно 1,05.
Рабочая напряженность при нормальных условиях работы ЛЭП определяется по формулам:
· для нерасщепленной фазы
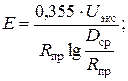кВ/см
· для расщепленной фазы
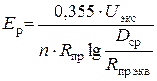, кВ/см
где U экс – среднее эксплуатационное (линейное) напряжение.
Если величина эксплуатационного напряжения неизвестна, то считают, что U экс = U ном.
Величина рабочей напряженности на фазах разная. В расчетах принимается величина наибольшей напряжённости:
E max = k расп× k расщ E,
где k расп – коэффициент, учитывающий расположение проводов на опоре;
k расщ – коэффициент, учитывающий конструкцию фазы.
Для проводов, расположенных в вершинах равностороннего треугольника или близкого к нему, k расп = 1. Для проводов, расположенных в горизонтально или вертикально, k расп = 1,05 – 1,07.
Для нерасщепленной фазы k расщ = 1. При расщепленной конструкции фазы коэффициент k расщ рассчитывается по формулам:
· при n = 2
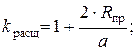
· при n = 3
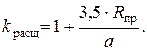
Напряжение, при котором возникает корона, рассчитывается по формуле:
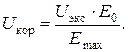
Чтобы повысить U кор нужно снизить E max. Для этого нужно увеличить либо радиус провода R пр либо Dср. В первом случае эффективно расщеплять провода в фазе. Увеличение D ср приводит к значительному изменению габаритов ЛЭП. Мероприятие малоэффективно, так как D ср находится под знаком логарифма.
Если E max > E 0, то работа ЛЭП является неэкономичной из-за потерь мощности на корону. Согласно ПУЭ, корона на проводах отсутствует, если выполняется условие:
E max £ 0,9 E 0 (m =0,82, d = 1).
При проектировании выбор сечений проводов выполняют таким образом, чтобы короны в хорошую погоду, не было. Так как увеличение радиуса провода является основным средством снижения DPкор, то установлены минимально допустимые сечения по условиям короны: при напряжении 110 кВ – 70мм2, при напряжении 150 кВ – 120мм2, при напряжении 220 кВ – 240мм2.
Величина погонной активной проводимости рассчитывается по формуле:
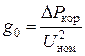, См/км.
Активная проводимость участка сети находится следующим образом:
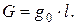
При расчете установившихся режимов сетей напряжением до 220кВ активная проводимость не учитывается – увеличение радиуса провода снижает потери мощности на корону практически до нуля. При U ном ³ 330кВ увеличение радиуса провода приводит к значительному удорожанию ЛЭП. Поэтому в таких сетях расщепляют фазу и учитывают в расчетах активную проводимость.
В кабельных ЛЭП расчет активной проводимости выполняется по тем же формулам, что и для воздушной ЛЭП. Природа потерь активной мощности иная.
В кабельных линиях DP вызываются явлениями, происходящими в кабеле за счет тока абсорбции. Для КЛЭП диэлектрические потери указываются заводом – изготовителем. Диэлектрические потери в КЛЭП учитываются при U ³ 35 кВ.
Реактивная (ёмкостная проводимость)
Реактивная проводимость обусловлена наличием емкости между фазами и между фазами и землей, так как любую пару проводов можно рассматривать как конденсатор.
Для ВЛЭП величина погонной реактивной проводимости рассчитывается по формулам:
· для нерасщепленных проводов
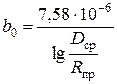, См/км;
· для расщеплённых проводов
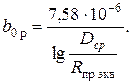
Расщепление увеличивает b 0 на 21¸33%.
Для КЛЭП величина погонной проводимости чаще рассчитывается по формуле:
b 0 = w × C 0.
Величина емкости C 0 приводится в справочной литературе для различных марок кабеля.
Реактивная проводимость участка сети рассчитывается по формуле:
В = b 0× l.
У воздушных ЛЭП значение b 0 значительно меньше, чем у кабельных ЛЭП, мало, так как D ср ВЛЭП >> D ср КЛЭП.
Под действием напряжения в проводимостях протекает ёмкостный ток (ток смещения или зарядный ток):
I c= В × U ф.
Величина этого тока определяет потери реактивной мощности в реактивной проводимости или зарядную мощность ЛЭП:
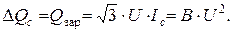
В районных сетях зарядные токи соизмеримы с рабочими токами. При U ном = 110 кВ, величина Q с составляет около 10% от передаваемой активной мощности, при U ном = 220 кВ – Q с ≈ 30% Р. Поэтому ее нужно учитывать в расчетах. В сети номинальным напряжением до 35 кВ величиной Q с можно пренебречь.
Схема замещения ЛЭП
Итак, ЛЭП характеризуется активным сопротивлением R л, реактивным сопротивлением линии х л, активной проводимостью G л, реактивной проводимостью В л. В расчетах ЛЭП может быть представлена симметричными П- и Т- образными схемами (рис. 4.6).
 |
П – образная схема применяется чаще.
В зависимости от класса напряжения теми или иными параметрами полной схемы замещения можно пренебречь (см. рис. 4.7):
· ВЛЭП напряжением до 220 кВ (D Р кор» 0);
· ВЛЭП напряжением до 35кВ (D Р кор» 0, D Q c» 0);
· КЛЭП напряжением 35кВ (реактивное сопротивление» 0)
· КЛЭП напряжением 20 кВ (реактивное сопротивление» 0, диэлектрические потери» 0);
· КЛЭП напряжением до 10 кВ (реактивное сопротивление» 0, диэлектрические потери» 0, D Q c» 0).
 |
Лекция № 5
