В данной работе изучается прямой центральный удар двух шаров, подвешенных в виде маятников, причем один из них занимает правое положение (шар1), другой – левое (шар2), рис. 9.2,а.
В опытах первый шар массой m 1 отклоняется на некоторый угол α 0 и фиксируется в этом состоянии электромагнитом. После отключения электромагнита происходит соударение первого шара с покоящимся вторым шаром массы m 2.
При столкновении шаров некоторая часть их механической энергии теряется, переходя во внутреннюю энергию, а другая часть механической энергии в соответствии с законом сохранения импульса перераспределяется между шарами.
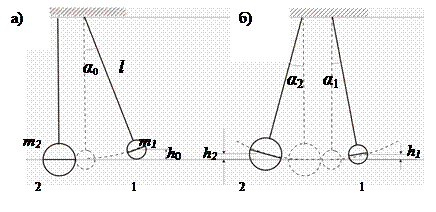
Рис.9.2.
|
а) исходное положение шаров 1 и 2; б) положение шаров при максимальном их отклонении после удара.
Пусть после соударения максимальные углы отклонения подвешенных шаров от вертикали соответственно равны α 1 и α 2 (см. рис.9.2,б). Потерянная кинетическая энергия при столкновении шаров равна:
,
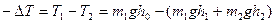где h 0= l 1(1- cosα0), h 1= l 1(cosα1), h 2= l 2(1- cosα2).
В условиях опыта l1 = l2 = l. Применяя формулу (9.5) и учитывая, что υ2=0 (скорость второго шара перед ударом) и m1υ12 /2= m1gh0, можно написать:
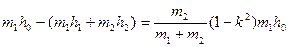
Отсюда для коэффициента восстановления получим:
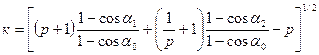, (9.6)
где p = m1 / m2, или
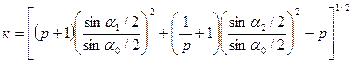(9.7)
По найденному коэффициенту восстановления можно судить о характере удара.
Порядок выполнения работы
1. Отрегулировать положение шаров таким образом, чтобы в состоянии покоя указатели шаров совпадали с нулевыми делениями угловых шкал, а при соударении – получался прямой центральный удар.
2. Отклонить правый шар до соприкосновения с электромагнитом (угол α 0).
3. Нажать клавишу «Сброс», а затем, убедившись, что левый шар находится в состоянии покоя, нажать клавишу «Пуск».
4. Записать угол отскока левого шара α 2 и показания индикатора «Время», соответствующее длительности удара τ.
5. Повторить п.п. 2-4 3-5 раз при том же значении угла α0 отклонения правого шара.
6. Повторить п.п. 2-4 3-5 раз с тем, чтобы записать значения угла α1, отклонения правого шара и τ.
7. Усреднить значения углов α 1i, α 2i и τ i, а величины < α 1>, < α 2>, < τ > и α 0 поместить в таблицу 1.
8. Изменить угол α 0 и повторить пункты 2-7.
9. По формуле (9.7) найти коэффициент восстановления k и занести его в табл.9.1.
10. Осуществить абсолютно неупругий удар. Для этого металлические шары заменить на пластилиновые. Для этого необходимо:
11. Отключить подвешенные металлические шары от электронного блока прибора и снять их со стержней вместе с их опорными призмами и аккуратно уложить их в коробку.
12. Подвесить пластилиновые шары, но теперь уже на один и тот же опорный стержень, причем чтобы призмы одного из шаров находились между призмами подвески другого шара.
13. Снова отрегулировать положение шаров с тем, чтобы обеспечить прямой центральный удар.
14. Левую шкалу углового отсчета передвинуть до соприкосновения с правой.
15. В 3-4 опытах произвести измерение углового отклонения α слипшихся после удара шаров при двух значениях первоначального угла отклонения α0 правого шара, при этом угол α отсчитывается по отклонению центра масс шаров.
16. Занести в табл. 9.2 усредненные значения величины α для каждого α 0.
17. Определить массу шаров путем взвешивания.
18. Убедиться в том, что равенство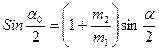 
, вытекающее из закона сохранения импульса, практически выполняется. Здесь m 1- масса налетающего пластилинового шара, m 2 – покоящегося шара.
19. Рассчитать долю η потерянной механической энергии при абсолютно неупругом ударе по формуле
.
Таблица 9.1
| Тела | α 0 | α 1 | α 2 | τ | k |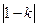 
| Характер удара |
| Металлические шары | |||||||
Табл. 9.2
| Тела | m 1, г | m 2, г | α 0 | α | k | η | Характер удара |
| Пластилиновые шары | |||||||
Контрольные вопросы
1. Выполняется ли закон сохранения импульса и механической энергии: а) для упругих столкновений б) для неупругих?
2. Что подразумевается под центральным ударом двух шаров?
3. Как определить скорости тел после прямого центрального абсолютно упругого удара? Какова роль законов сохранения в этом случае?
4. Два шара подвешены на параллельных нитях одинаковой длины так, что они соприкасаются. Массы шаров известны. Первый шар отклоняют так, что его центр тяжести поднимается на высоту H, и отпускают. На какую высоту поднимутся шары после соударения, если: а) удар упругий б) удар неупругий?
10. ИССЛЕДОВАНИЕ ДВИЖЕНИЯ ТЕЛ В ЖИДКОСТИ
Лабораторная работа 1.10.
Цель работы: освоение методов определения коэффициента вязкости и числа Рейнольдса.
Принадлежности: стеклянный цилиндр с жидкостью, микрометр, секундомер, шарики.
