Лабораторная работа № 1.2.
Цель работы: исследовать деформацию кручения цилиндрического тела и установить связь между крутящим моментом и углом закручивания. Определить модуль сдвига образца.
Оборудование: крутильный маятник, измеритель периода крутильных колебаний системы, набор металлических дисков с известными моментами инерции, стальная проволока, электромагнит.
Теоретическое введение
Под действием приложенных сил всякое твердое тело деформируется, т.е. изменяет свои размеры и форму. Если после прекращения действия сил тело принимает первоначальные размеры и форму, то деформация называется упругой. В противном случае – неупругой (пластической). Упругие деформации имеют место в том случае, если деформирующая сила не превосходит некоторую определенную для каждого конкретного тела предельную силу Fпр.
При деформациях происходит смещение частиц, находящихся в узлах кристаллических решеток твердых тел, из первоначальных положений равновесия в новые. Этому препятствуют силы электромагнитного взаимодействия между частицами, вследствие чего в деформированном теле возникают упругие внутренние силы, которые уравновешивают внешние силы, приложенные к телу.
Пусть на выделенный элемент поверхности dS некоторого сечения тела действует упругая сила dFупр, а dFn и dFτ – нормальная и касательная составляющие этой силы (рис. 2.1).
Величину σ = dFn/dS называют нормальным напряже- нием в окрестности заданной точки, а величину τ = dFτ/dS – касательным напряжением. Согласно определению единицей измерения напряжения в системе СИ является [ σ ] = [ τ ] = = H/м2 = Па.
Нормальные напряжения вызываются деформациями растяжения-сжатия тела, а касательные – смещением плоских слоев твердого тела параллельно некоторой плоскости сдвига без их искривления и изменения размеров. В связи с этим выделяют два основных вида деформации твердого тела: – растяжения - сжатия и деформацию сдвига. Изгиб, кручение и более сложные деформации относятся либо к одному из двух основных неоднородных деформаций, либо к их наложению.
Мерой деформации растяжения-сжатия является относительное удлинение (сжатие) ε = Δ l / l (рис.2.2а).
 | |||||
 | |||||
| |||||
Мерой деформации сдвига является угол сдвига γ, выраженный в радианах (рис.2.2б). Для малых деформаций γ ≈ tgγ = a/b, где а – абсолютный сдвиг, b - расстояние между параллельными плоскостями слоя. Относительные деформации ε и γ – безразмерные величины. Иногда их представляют в %. Для малых (упругих) деформаций растяжения-сжатия и сдвига, как показывают опыты, существует линейная связь между напряжением и соответствующей относительной деформацией:
σ = Еε, (2.1)
τ = Gγ (2.2)
Величины Е и G называют модулями упругости материала. Первый модуль Е – нормальным (модулем Юнга), второй G – модулем сдвига. Из (2.1) и(2.2) видно, что размерность модулей упругости та же, что и для напряжения.
Между модулями упругости G и E имеется связь:
. (2.3)
Величину μ, равную отношению относитель- ного сужения (расшире- ния) Δd/d к относительному продольному удлинению (сжатию) называют коэффициентом Пуассона:
, (2.4)
где Δd= d - d َ ′.
Рассмотрим деформации, вызываемые кручением твердого цилиндрического тела. Кручением называется деформация образца с одним закрепленным концом (а может быть условно) под действием пары сил, плоскость которой перпендикулярна оси образца. Кручение состоит в относительном повороте параллельных друг другу сечений, проведенных перпендикулярно к оси образца. Деформация кручения является неоднородной. Она увеличивается при удалении от оси поворотов элементов образца.
Закон Гука для деформации кручения записывается в виде
, (2.5) где ƒ - постоянная кручения, 
- абсолютный угол кручения образца.
Постоянная кручения показывает, какой момент сил нужно приложить, чтобы закрутить проволоку на угол в 1 рад. В отличие от модулей Юнга и сдвига эта величина зависит не только от материала, но и от геометрических размеров проволоки.
Деформацию кручения можно свести к деформации сдвига. Получим выражение для постоянной кручения ¦.
Стержень (рис.2.4) можно представить состоящим из
множества цилиндрических оболочек (трубок), каждая из которых характеризуется радиусом r, длиной L и толщиной dr. Площадь основания трубки
dS = 2p r dr, (2.6)
а момент касательных упругих сил, действующих в этом основании,
, (2.7)
где 
- напряжение сдвига в этом сечении.
Каждый продольный элемент цилиндрической трубки поворачивается на угол
. (2.8)
По закону Гука для сдвига получим
. (2.9)
Итак, момент сил, действующих на цилиндрическую трубку, равен
. (2.10)
O
C
φ
L
O
|
Полный же момент сил, действующих на проволоку (стержень) радиуса R, найдется интегрированием выражения (2.10):
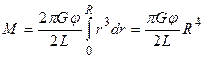. (2.11)
Имея соотношения (2.5) и (2.11), получим выражение для постоянной кручения образца
. (2.12)
Экспериментально модуль кручения можно измерить, наблюдая крутильные колебания маятника.
.
