В электрических цепях переменного тока при параллельном соединении реактивных сопротивлений может возникнуть резонанс токов. Это происходит в том случае, когда в одних ветвях преобладает реактивное индуктивное сопротивление, а в других – реактивное емкостное сопротивление. При взаимной компенсации реактивных токов в параллельно включенных элементах возникающий резонанс называется резонансом токов.
Характерные особенности резонанса токов проанализируем на примере параллельного колебательного контура с потерями энергии, обусловленными резисторами (рис. 1). Для упрощения анализа в параллельный контур введем резисторы с одинаковыми сопротивлениями 
Эквивалентная проводимость параллельного контура между точками «a» и «b» определяется выражением
Условие резонанса определяется равенством нулю мнимой части входной проводимости параллельного резонансного контура 
. Заменяя в выражении 
угловую частоту 
на резонансную частоту 
, условие резонанса перепишем в виде
.
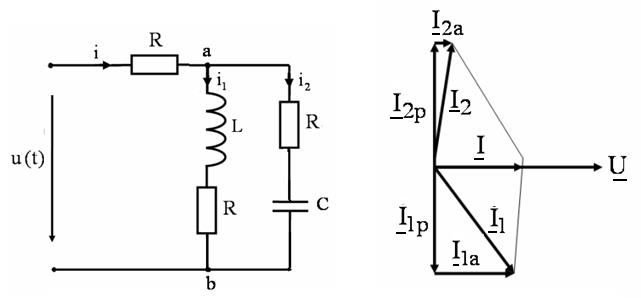
Рис. 1 Рис.2
Решение уравнения относительно дает выражение
где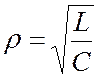 
– волновое (характеристическое) сопротивление.
В идеальном контуре, когда 
резонансная частота 
принимает такое же значение, как и в последовательном резонансном контуре. Ток на неразветвленном участке цепи протекать не будет, так как 
.
При резонансе эквивалентное сопротивление параллельного контура между точками «а» и «б» определяется выражением
Если активные сопротивления, включенные в параллельные ветви не равны между собой, то выражения для расчета 
и 
получаются более сложными.
Ток на неразветвленном участке цепи при резонансе определяется выражением
.
Токи в параллельных ветвях при резонансе определяются, используя закон Ома
.
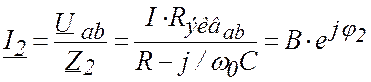При малых значениях сопротивлений 
, когда выполняются неравенства 
и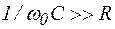 
, угол сдвига фаз между токам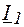и 
и 
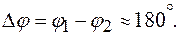
Из векторной диаграммы (рис. 2) видно, что при малых значениях ток 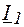будет отставать по фазе от напряжения 
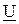почти на 90 0, а ток – соответственно опережать напряжение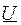 
почти на угол 
Описание лабораторного стенда и рабочее задание
1. Собрать схему параллельного резонансного контура, используя съемную панель лабораторного стенда (рис. 3) и расположенные на ней тумблеры 
– 
. Внимание! При сборке схемы с помощью тумблеров 
следует учитывать, что перевод тумблера в верхнее положение соответствует замыканию ключа на участке цепи.
На съемной панели параметры цепи таковы:
, 
, 
, 
.
2. Подключить схему непосредственно к генератору низкой частоты (ГНЧ). Установить с помощью ручки управления ГНЧ и вольтметра PV1 действующее значение напряжения в диапазоне 
В.
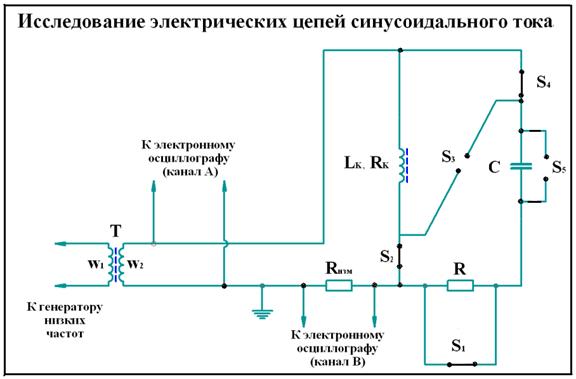
Рис. 3
3. Используя исходные данные пункта 1 рабочего задания, рассчитать для параллельного резонансного контура:
· резонансную частоту 
;
· волновое сопротивление 
;
· добротность резонансного контура 
;
· параметр затухания 
;
· реактивные (
и 
) и активные (
и 
) составляющие токов в параллельных ветвях;
· токи в параллельных ветвях (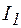
и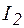 
), а также ток 
на неразветвленном участке цепи при резонансе;
· добротность резонансного контура 
.
При выполнении расчетов по пункту 2 рабочего задания использовать следующие соотношения:
, 
, 
, 
,
, 
,
, 
, 
.
4. В цепи (рис. 5), находящейся под напряжением, изменяя частоту ГНЧ с помощью ручек управления «Грубо» и «Точно» в окрестности расчетного значения 
, найти резонансную частоту опытным путем, так, чтобы на экране осциллографа угол сдвига фаз между напряжением на зажимах вторичной обмотки трансформатора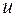 
(канал A) и напряжением 
(канал B) был близок нулю.
5. В электрической цепи (рис. 3) измерить ток 
, входное напряжение 
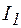вольтметром PV1, токи в параллельных ветвях и 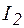амперметром PA1, последовательно подсоединяя его к участку цепи, а также угол сдвига фаз между приложенным напряжением и напряжением на сопротивлении 
с помощью осциллографа:
,
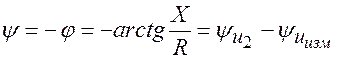варьируя частоту ГНЧ 
(где 
= 0, 1, 2) от резонансной частоты через интервалы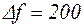 
Гц с помощью ручек управления «Грубо» и «Точно».
Результаты измерений занести в таблицу.
| Частота, Гц | Опыт | Расчет | ||||||||||
 ,
В
|  ,
В
|  ,
мА
|  ,
мА
|  ,
град
|  ,
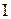мА
|  ,
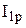мА
|  ,
мА
|  ,
Сим
|  ,
Сим
|  ,
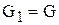Сим
|  ,
Сим
| |
Таблица
6. Дополнить таблицу пункта 4 рабочего задания расчетными данными, определив ток на неразветвленном участке цепи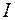 
, активную 
и реактивную 
составляющие тока в катушке индуктивности, реактивные 
и 
проводимости параллельных ветвей, эквивалентные реактивную 
и активную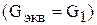 
проводимости цепи.
7. По данным таблицы 1 пункта 5 рабочего задания построить графики зависимост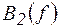и 
, 
, 
и 
.
8. По данным таблицы 1 пункта 5 рабочего задания построить графики зависимосте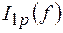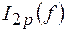й 
, 
, 
и 
.
Вопросы к защите
1. Запишите условие резонанса токов для параллельного контура.
2. Что такое резонанс токов?
3. Применение явления резонанса токов.
4. Как определяется знак угла ?
5. Приведите формулы, по которым можно рассчитать активную, реактивную и полную проводимости параллельного контура на любой частоте, (рис. 1).
6. Каким образом можно экспериментально изменить резонансную частоту?
7. Какими способами можно определить добротность параллельного RLC – контура?
8. Почему входное сопротивление идеального контура бесконечно большое?
9. Построить векторную диаграмму токов и напряжений для идеального и реального контуров.
Содержание отчета
1. Выполнение домашнего задания.
2. Электрическая схема испытаний резонанса токов. Определение резонансной частоты опытным и расчетным путем. Сопоставление данных расчета и эксперимента.
3. Построение графиков, характеризующих явление резонанса токов, по данным таблицы испытаний.
4. Определение добротности и волнового сопротивления резонансного контура.
5. Выводы.
Лабораторная работа № 5
