В цепи переменного тока при подаче напряжения  возникает ток
возникает ток 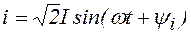 . В неразветвленной электрической цепи переменного тока, содержащей элементы с параметрами: активное сопротивление R, индуктивность L и емкость C (рис. 1), напряжение питающей сети равно векторной сумме напряжений, действующих на участках цепи.
. В неразветвленной электрической цепи переменного тока, содержащей элементы с параметрами: активное сопротивление R, индуктивность L и емкость C (рис. 1), напряжение питающей сети равно векторной сумме напряжений, действующих на участках цепи.

Рис. 1. Рис. 2.
В соответствии с этим выражение для напряжения, подводимого к такой электрической цепи, может быть записано по второму закону Кирхгофа в комплексной форме
 ,
,
где  ,
,  ,
,  – комплексные напряжения на участках цепи, определяемые как произведения комплексного тока на соответствующие сопротивления; R,
– комплексные напряжения на участках цепи, определяемые как произведения комплексного тока на соответствующие сопротивления; R,  – активное и реактивные индуктивное и емкостное сопротивления;
– активное и реактивные индуктивное и емкостное сопротивления; 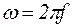 – угловая частота; f – частота напряжения.
– угловая частота; f – частота напряжения.
По уравнению для комплексного напряжения на входе цепи можно построить векторную диаграмму тока и напряжений электрической цепи. Для этого следует помнить, что умножение вектора напряжения на множитель (+ j) соответствует повороту его относительно вектора тока на угол  в направлении отсчета положительных углов (против часовой стрелки), а умножение на множитель (– j) – соответственно повороту вектора напряжения на угол
в направлении отсчета положительных углов (против часовой стрелки), а умножение на множитель (– j) – соответственно повороту вектора напряжения на угол  по часовой стрелке. Вектор напряжения
по часовой стрелке. Вектор напряжения  на активном сопротивлении при этом совпадает с вектором тока
на активном сопротивлении при этом совпадает с вектором тока  . Угол
. Угол  – угол между векторами тока и напряжения, подводимого к цепи (откладывается от вектора тока к вектору напряжения). Векторная диаграмма для электрической цепи (рис. 1) представлена на рисунке 2.
– угол между векторами тока и напряжения, подводимого к цепи (откладывается от вектора тока к вектору напряжения). Векторная диаграмма для электрической цепи (рис. 1) представлена на рисунке 2.
Уравнение для подводимого к электрической цепи комплексного напряжения с учетом его составляющих преобразуется к виду

или к виду уравнения, записанного в комплексной форме по закону Ома для всей цепи:

где  – комплексное сопротивление электрической цепи переменного тока.
– комплексное сопротивление электрической цепи переменного тока.
Модуль комплексного сопротивления (полное сопротивление) цепи переменного тока определяется уравнением
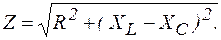
Из этого выражения следует, что полное сопротивление электрической цепи переменного тока зависит не только от параметров цепи, но и от частоты питающего напряжения, причем для линейной электрической цепи значения как полного сопротивления, так и его составляющих не зависят от подводимого напряжения.
Взаимосвязь между действующими значениями напряжения и полным сопротивлением цепи определяется соотношениями  или
или 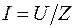 .
.
Из треугольника напряжений (рис. 2) можно получить треугольник сопротивлений, разделив стороны этого треугольника на комплексный ток  . Из треугольника сопротивлений следует, что
. Из треугольника сопротивлений следует, что
 .
.
Полученные выражения показывают, что угол сдвига фаз  между током
между током  и напряжением
и напряжением 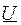 питающей цепи зависит от характера сопротивлений, включенных в цепь переменного тока.
питающей цепи зависит от характера сопротивлений, включенных в цепь переменного тока.
Умножив стороны треугольника сопротивлений на квадрат тока в цепи  , получим треугольник мощностей. Из треугольника мощностей можно установить взаимосвязь между активной
, получим треугольник мощностей. Из треугольника мощностей можно установить взаимосвязь между активной  , полной
, полной  и реактивной
и реактивной  мощностями электрической цепи. Активная мощность цепи переменного тока
мощностями электрической цепи. Активная мощность цепи переменного тока  , отсюда
, отсюда  . Реактивная составляющая полной мощности цепи находится как разность реактивной индуктивной
. Реактивная составляющая полной мощности цепи находится как разность реактивной индуктивной  и реактивной емкостной
и реактивной емкостной 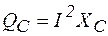 ее составляющих
ее составляющих  .
.
Выражение для полной мощности цепи переменного тока в комплексной форме записывают в следующем виде:
 или
или 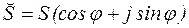 ,
,
где  – модуль полной мощности цепи переменного тока.
– модуль полной мощности цепи переменного тока.
В электрических цепях переменного тока имеются также цепи с параллельным соединением потребителей электроэнергии, при котором все потребители находятся под одним и тем же напряжением. При этом на ток в цепи каждого из потребителей не влияет их количество. Значение тока в каждом из них определяется только значениями соответствующих сопротивлений и значением подводимого напряжения. Сопротивления в цепях переменного тока обычно носят комплексный характер. Пример электрической цепи переменного тока с параллельным соединением сопротивлений приведен на рисунке 3.
Рассматривая отдельные параллельные ветви этой цепи как независимые электрические цепи, для каждой из них можно построить векторную диаграмму (рис. 4). При этом вектор тока  отстает по фазе от вектора напряжения
отстает по фазе от вектора напряжения 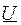 на угол
на угол 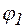 (активно – индуктивный характер сопротивления ветви), а вектор тока
(активно – индуктивный характер сопротивления ветви), а вектор тока  совпадает по фазе вектором напряжения
совпадает по фазе вектором напряжения 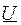 (активный характер сопротивления ветви).
(активный характер сопротивления ветви).


Ток  можно разложить на активную
можно разложить на активную  и реактивную
и реактивную  составляющие. Учитывая, что
составляющие. Учитывая, что  ,
,  и
и  , из векторной диаграммы находим:
, из векторной диаграммы находим:
 ,
,
где  – активная проводимость первой ветви электрической цепи.
– активная проводимость первой ветви электрической цепи.
Реактивная составляющая тока  определяется из соотношения
определяется из соотношения
 ,
,
где  – реактивная проводимость;
– реактивная проводимость; 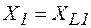 – реактивное сопротивление первой ветви.
– реактивное сопротивление первой ветви.
По аналогичным соотношениям определяются активная и реактивная составляющие тока 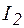 ветви, а именно:
ветви, а именно:
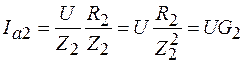 ,
,  ,
,
где  и
и 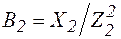 – соответственно активная и реактивная проводимость второй ветви (так как реактивное сопротивление второй ветви
– соответственно активная и реактивная проводимость второй ветви (так как реактивное сопротивление второй ветви  , то реактивная проводимость
, то реактивная проводимость  ).
).
При этом токи в параллельных ветвях  и
и 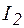 будут:
будут:
 ;
;  ,
,
где  ,
,  – модули полных проводимостей соответствующих параллельных ветвей.
– модули полных проводимостей соответствующих параллельных ветвей.
Согласно первому закону Кирхгофа для точки разветвления (узла) электрической цепи с параллельным соединением сопротивлений, общий ток может быть представлен в виде векторной суммы:
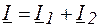 ,
,
где  и
и  – комплексные токи в соответствующих параллельных ветвях электрической цепи.
– комплексные токи в соответствующих параллельных ветвях электрической цепи.
Для рассматриваемой электрической цепи (рис. 3) можно получить выражение для общего тока  . Определяя комплексные проводимости
. Определяя комплексные проводимости 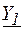 и
и 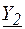 параллельных ветвей через комплексные сопротивления
параллельных ветвей через комплексные сопротивления
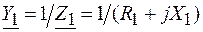 и
и  ,
,
получим
 .
.
Для произвольного числа параллельных ветвей активная проводимость электрической цепи  оказывается равной сумме активных проводимостей всех параллельных ветвей
оказывается равной сумме активных проводимостей всех параллельных ветвей  , а реактивная проводимость цепи равна алгебраической сумме реактивных проводимостей всех параллельных ветвей
, а реактивная проводимость цепи равна алгебраической сумме реактивных проводимостей всех параллельных ветвей  . Модуль полной проводимости цепи определяется из выражения
. Модуль полной проводимости цепи определяется из выражения
 .
.
При этом полная проводимость цепи является также и величиной обратной ее полному сопротивлению  . Разделив каждый вектор
. Разделив каждый вектор  тока на векторной диаграмме (рис. 4) на вектор напряжения
тока на векторной диаграмме (рис. 4) на вектор напряжения  , можно получить треугольник проводимостей для данной цепи. В качестве примера на рис. 5 представлен треугольник проводимостей для первой ветви схемы (рис. 3). Из треугольника проводимостей следует, что
, можно получить треугольник проводимостей для данной цепи. В качестве примера на рис. 5 представлен треугольник проводимостей для первой ветви схемы (рис. 3). Из треугольника проводимостей следует, что 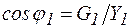 , а
, а  . С учетом этого полная
. С учетом этого полная 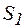 , активная
, активная  и реактивная
и реактивная 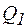 мощности первой ветви электрической цепи могут быть определены через соответствующие проводимости
мощности первой ветви электрической цепи могут быть определены через соответствующие проводимости
 ,
,  ,
, 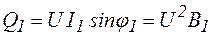 .
.
Полная  , активная
, активная 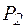 и реактивная
и реактивная 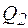 мощности второй ветви электрической цепи определяются выражениями
мощности второй ветви электрической цепи определяются выражениями
 ,
,  .
.
Модуль полной мощности всей цепи при этом будет
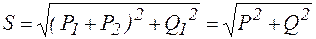 .
.
Описание лабораторного стенда и рабочее задание
1. Собрать схему, приведенную на рисунке 5. При сборке схемы использовать обмотку с индуктивностью  сопротивлением обмоточного провода
сопротивлением обмоточного провода  , резистор с сопротивлением
, резистор с сопротивлением  . С зажимов вторичной обмотки однофазного трансформатора подать на схему переменное синусоидальное напряжение промышленной частоты
. С зажимов вторичной обмотки однофазного трансформатора подать на схему переменное синусоидальное напряжение промышленной частоты 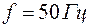 .
.

Рис. 5
2. В электрической цепи (рис. 5) произвести измерения электрических величин:
· действующие значения тока 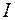 , входного напряжения
, входного напряжения 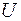 и напряжения на катушке индуктивности
и напряжения на катушке индуктивности  . Для измерения силы тока воспользоваться цифровым амперметром, а напряжения – цифровым вольтметром;
. Для измерения силы тока воспользоваться цифровым амперметром, а напряжения – цифровым вольтметром;
· активную мощность  , потребляемую цепью, то есть среднее значение мгновенной мощности за период входного напряжения с помощью цифрового ваттметра;
, потребляемую цепью, то есть среднее значение мгновенной мощности за период входного напряжения с помощью цифрового ваттметра;
· угол сдвига фаз  между напряжением на резисторе и входным напряжением, переключив ваттметр на фазометр. Угол
между напряжением на резисторе и входным напряжением, переключив ваттметр на фазометр. Угол 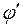 совпадает с углом сдвига фаз между током и напряжением источника питания
совпадает с углом сдвига фаз между током и напряжением источника питания  . Поскольку аргумент
. Поскольку аргумент  комплексного сопротивления
комплексного сопротивления  собранной на стенде цепи определяется как сдвиг фаз между входным напряжением и током
собранной на стенде цепи определяется как сдвиг фаз между входным напряжением и током  , то угол сдвига фаз
, то угол сдвига фаз  .
.
Результаты измерений занести в графу «Опыт» таблицы 1.
3. Заполнить таблицу 1 пункта 2 рабочего задания, используя расчетные соотношения



Таблица 1
| Опыт | Расчет | |||||||
| U, В | I, мА | P, Вт |  ,
В ,
В
| 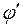 ,
град. ,
град.
|  В
В
|   ,
В ,
В
| 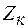 ,
Ом ,
Ом
|  ,
Ом ,
Ом
|
Окончание табл. 1
| Расчет | ||||||||
| XК, Ом | RЭ, Ом | XЭ, Ом | ZЭ, Ом |  ,
град. ,
град.
|

| S, ВА | Q, вар |  ,
Гн ,
Гн
|
4. По данным таблицы 1 пункта 3 рабочего задания построить в масштабе векторную диаграмму для электрической цепи (рис. 5).
5. Собрать схему, приведенную на рисунке 6. При сборке схемы использовать конденсатор емкостью  и резистор с сопротивлением
и резистор с сопротивлением  .
.

Рис. 6.
6.  В цепи, находящейся под напряжением, произвести измерения электрических величин, аналогично пункту 2 рабочего задания. Результаты эксперимента занести в таблицу 2.
В цепи, находящейся под напряжением, произвести измерения электрических величин, аналогично пункту 2 рабочего задания. Результаты эксперимента занести в таблицу 2.
7. Дополнить таблицу 2 расчетными данными, используя для определения активных и реактивных составляющих напряжений и токов соответственно в последовательной (рис. 7) и параллельной (рис. 8) эквивалентных схемах замещения цепи (рис. 6) следующие соотношения:

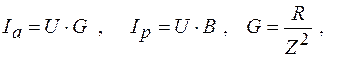

8. По данным таблицы 2 пункта 7 рабочего задания построить в масштабе векторную диаграмму для электрической цепи (рис. 6).
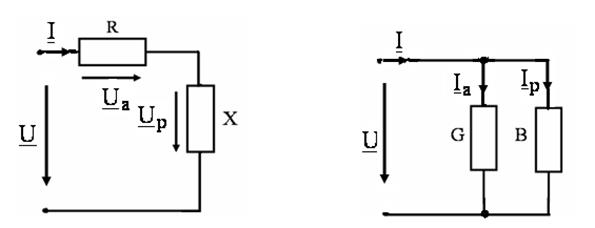
Рис. 7 Рис. 8.
Вопросы к защите
1. Что такое емкостное, индуктивное и комплексное сопротивления?
2. Как зависят реактивные сопротивления конденсатора и катушки индуктивности от частоты? Нарисуйте графики этих зависимостей.
3. Нарисуйте треугольники сопротивлений для последовательных  и
и  электрических цепей.
электрических цепей.
4. Чему равны активная, реактивная, полная и комплексная мощности в идеальных индуктивных и емкостных элементах?
5. Для электрической цепи (рис. 9) записать комплексы тока  , напряжений
, напряжений  и
и  , если
, если  и
и  .
.
6. Определить по заданному входному напряжению U напряжение  в электрической цепи (рис. 10), если сопротивления участков
в электрической цепи (рис. 10), если сопротивления участков  .
.

Рис. 9 Рис. 10
7. По качественной временной диаграмме тока (рис. 11), проходящего через конденсатор, постройте качественные временные зависимости напряжения, мощности и энергии, запасенной в конденсаторе.

Рис. 11
Содержание отчета
1. Выполнение домашнего задания.
2. Электрические схемы испытаний  и
и  цепей, а также результаты измерений (тока, напряжений на участках цепи, угла сдвига фаз между напряжением и током на входе цепи).
цепей, а также результаты измерений (тока, напряжений на участках цепи, угла сдвига фаз между напряжением и током на входе цепи).
3. Сопоставление расчетных и экспериментальных данных в таблицах 1 и 2, используя расчеты  и
и  цепей по действующим значениям токов и напряжений. Построение в масштабе векторных диаграмм для
цепей по действующим значениям токов и напряжений. Построение в масштабе векторных диаграмм для  и
и  цепей.
цепей.
4. Выводы.
Лабораторная работа № 3
РЕЗОНАНС НАПРЯЖЕНИЙ
Цель работы: Установление условийрезонанса напряжений. Исследование частотныхзависимостей напряжений на элементах последовательного резонансного контура.
Домашнее задание
1. Укажите необходимые и достаточные условия для возникновения в электрических цепях переменного синусоидального тока резонанса напряжений.
2. Охарактеризуйте возможные способы получения резонанса напряжений в электрической цепи. Приведите расчетные соотношения для определения значений искомых величин при резонансе напряжений.
3. Каким образом можно обнаружить резонанс напряжений?
4. Что представляет собой амплитудно-частотная характеристика (АЧХ) последовательного резонансного контура? Каким способом по АЧХ можно определить полосу пропускания (прозрачности) контура?
5. Что представляет собой фазочастотная характеристика (ФЧХ) последовательного резонансного контура? Почему идеальная ФЧХ в полосе пропускания должна быть линейной?






