22. Скопіюйте таблицю на наступний аркуш, назвіть ЙОГО Площа2, переробіть таблицю, щоб розв'язати задачу
Задача 5а. З курсу математики відомо, що для отримання точнішого значення площі значення кроку h потрібно зменшувати. Зменшіть значення h удвічі й обчисліть площу під кривою на тому ж самому проміжку.
Оскільки ім'я клітинки h та її значення діють у всій книзі, ім'я не можна застосувати на новому аркуші без деформації даних на попередньому. Тому кроку потрібно надати нове і наприклад V, і відповідно змінити формули в таблиці.
23. Збережіть книжку під назвою Задача5.
24. Продемонструйте п'ять аркушів викладачеві і закінчі роботу.
Контрольні запитання
1. Яке призначення формул в ЕТ? Яке значення функції МИН(5; 2; 13)?
2. Що таке копіювання формул? Яке значення функції СУММ(5; 2; 13)?
3. Які є категорії стандартних функцій?
4. Як клітинці надати ім'я?
5. Що таке діапазон клітинок? Наведіть приклади діапазонів.
6. Як скопіювати формулу з деякої клітинки в діапазон-стовпець?
7. Як виокремити діапазон? Яке значення функції МИН(15; 20; МАКС(1; 3; 5))?
8. Опишіть пріоритети виконання операцій у виразах.
9. Як вставити рядок у таблицю? Яке значення функції СУММ(12; МАКС(8; 12; 20))?
10. Як працює команда Підсумки даних?
11. Як скопіювати формулу з деякої клітинки в рядок?
12. Як вилучити стовпець чи рядок з таблиці?
13. Яке призначення приміток і як їх вставляти?
14. Як виконати пошук потрібних даних у таблиці?
15. Як нанести дані на географічну карту?
16. Як очистити клітинку? Яке значення функції МАКС(15; 40; 25)?
17. Як вилучити примітку?
18. Як користуватися командою Автофільтр?
19. Яке значення виразу СУММ(5; 10; 15) - 2*МИН(20; 40)?
20. Які є формати нанесення даних на географічні карти?
21. Наведіть приклади статистичних функцій.
22. Яке призначення кнопки Автосума?
23. Як забрати чи показати деталі у підсумковій таблиці?
24. Як скопіювати таблицю на інший аркуш?
25. Які математичні функції є в ЕТ? Яке значення виразу SIN(0) + 2*SQRT(9)?
26. Як заповнити стовпець числами, що утворюють арифметичну прогресію?
27. Як відцентрувати заговолок таблиці відносно стовпців?
28. Як задати режим відображення формул? Яке значення функції СРЗНАЧ(15; 20; МИН(25; 45))?
29. Як зберегти книжку на диску? Яке значення виразу СРЗНАЧ(МАКС(8; 12); МИН(4; 16))?
30. Як створити список користувача?
31. Як заховати стовпець? Яке значення функції СРЗНАЧ (15; 20; 25; 5; 10)?
32. Як заповнити стовпець чи рядок елементами списку користувача?
33. Яке значення виразу МАКС(15; 20; МИН(45; 25))?
34. Яким символом відокремлюють аргументи у функціях?
35. Яке значення функції СРЗНАЧ (15; МАКС(20; 25))?
Практична робота №4. MS Excel. Побудова діаграм
Мета
Ознайомитися з видами діаграм і вміти їх будувати за число вими даними з побудованих раніше таблиць.
План
1. Основні поняття про діаграми.
2. Головні типи діаграм.
3. Структура і форматування діаграми.
4. Створення діаграми.
Теоретичні відомості
1. Основні поняття про діаграми. Діаграми призначені для графічного відображення числових даних у звітах, на презен таційних, рекламних чи веб-сторінках тощо.
Діаграми поділяються на стандартні (найбільш поширені) та нестандартні (використовуються зрідка).
Є багато типів стандартних діаграм: гістограма, лінійна, І графік, кругова, точкова, з областями, кільцева, поверхнева пелюсткова, булькова, біржова, циліндрична, конічна, піра мідальна тощо. Кожний тип стандартної діаграми має декілька видів. Наприклад, гістограма, яка відображає дані у вигляді пропорційних відносно даних стовпців, може бути звичайною І (стовпці розташовані поряд), з накладеними стовпцями, нор мованою (усі стовпці даних накладені і їхня загальна висота при ймається за 100%), об'ємною звичайною, об'ємною накладеною, об'ємною нормованою, об'ємною з тривимірним ефектом.
З нестандартних використовують такі: блакитну кругову, блоки з областями, вирізані сектори, графік|гістограма, графік і з двома вертикальними осями, кольорові графіки, ширяючі брус ки тощо.
З виглядом і коротким описом кожної з діаграм рекомендуємо ознайомитися під час виконання першого кроку майстри побудови діаграм.
Найчастіше будують кругові, точкові, стовпцеві стандартні і діаграми різних видів.
2. Головні типи діаграм. Оскільки різновидів діаграм є де кілька десятків, ми розглянемо лише найважливіші (рис. 43).
Кругова діаграма відображає один виокремлений рядок чи стовпець числових даних з таблиці у вигляді круга із секторами.
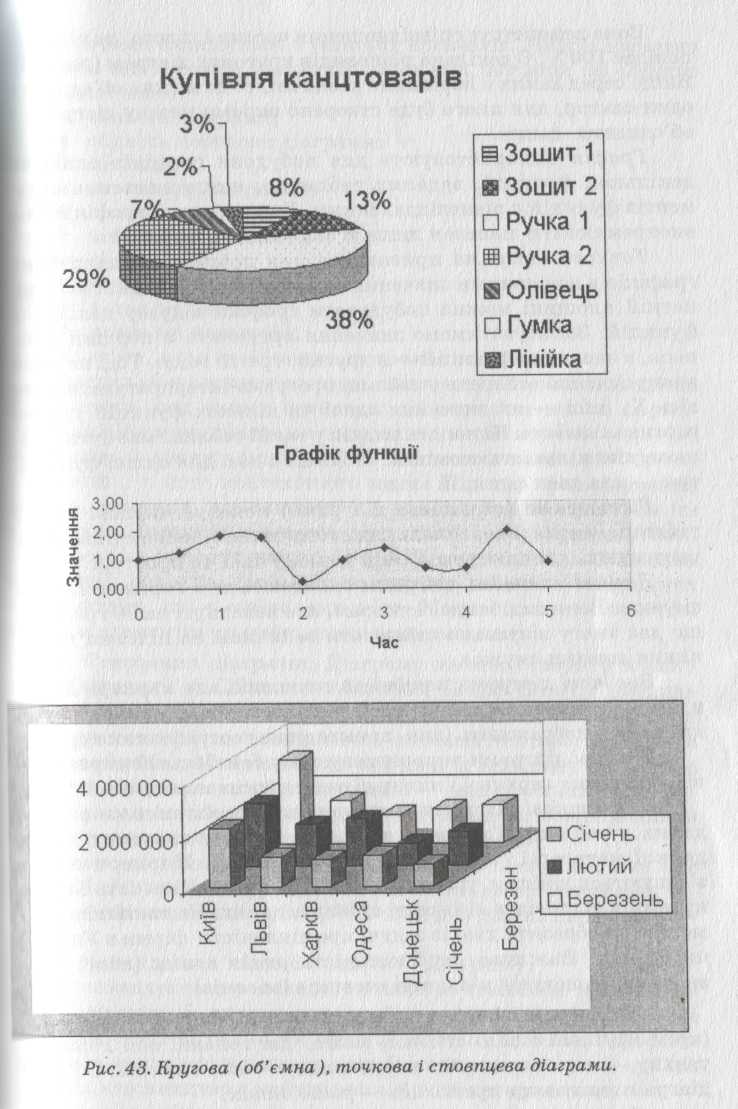

Вона демонструє співвідношення частин і цілого, де ціле від повідає 100%. Є декілька різновидів кругових діаграм (рис. 43). Якщо серед даних є порівняно незначні, то їх можна об'єднати в один сектор, для якого буде створено окрему меншу діаграму з об'єднаних даних.
Графік використовують для побудови графіків одної чи декількох функцій, заданих таблично, якщо значення аргу ментів функцій є рівновіддаленими. Для побудови графіків слід виокремлювати діапазон лише зі значеннями функцій.
Точкова діаграма призначена для побудови традиційних графіків з довільними значеннями аргумента. На одній коорди
Інатній площині можна побудувати графіки відразу декількох функцій. Записуватимемо значення аргумента в перший стов пець, а значення функцій — в другий, третій тощо. Тоді перший виокремлений стовпець у таблиці програма інтерпретуватиме як вісь X, інші — як значення одної чи кількох функцій уздовж вертикальної осі. Кількість рядків у такій таблиці має бути біль шою, ніж кількість стовпців. Стовпців є два для однієї функції три — для двох функцій і т.д.
Гістограма (стовпцева діаграма) показує числові дмім таблиці у вигляді вертикальних стовпчиків. її найчастіше викої ристовують для ілюстрації змін даних у часі чи просторі.
Лінійні звичайні діаграми складаються з горизонтальних смужок. Вони подібні до гістограм, але повернуті на 90 градусів що дає змогу візуально оцінювати величини на підставі порів няння довжин смужок.
Булькові діаграми подібні до точкових, але маркери даних в них — це круги чи сфери, діаметри яких пропорційні до даних які вони відображають (див. приклади на географічних картах).
Біржові діаграми використовують у банківській справі для відображення верхньої і нижньої межі курсів валют, акцій тощо
Пелюсткові діаграми мають стільки осей, скільки є рядів даних у таблиці. Уздовж осей відкладаються значення даних деякої категорії (тобто з деякого стовпця). Маркери даних з'єднуються лініями, утворюючи багатокутник. Кількість багато кутників відповідає кількості стовпців даних. На такій діаграмі можна відобразити дані із задачі про діяльність фірми в Україні чи Європі. Важливо, щоб кількість рядів даних (міст) була значно більшою від кількості стовпців (місяців).
3. Структура і форматування діаграми. Майже всі діаграми (крім кругової і пелюсткової) мають дві головні осі: горизон тальну — вісь категорій, вертикальну — вісь значень. Об'ємні І діаграми мають ще третю вісь — рядів даних.
Діаграма складається з багатьох елементів. Нижче наведено ті, назви яких можна прочитати на екрані, навівши на елемент вказівник миші:
♦ область діаграми;
♦ область побудови діаграми;
♦ легенда;
♦ заголовок діаграми;
♦ вісь ряду даних;
♦ вісь категорій;
♦ вісь значень;
♦ маркери даних;
♦ назва осі значень;
♦ назва осі категорій;
♦ стіни, кути (в об'ємних діаграмах) тощо.
Вигляд усіх елементів можна змінювати. Елементи діаграми є об'єктами, над якими визначені дії переміщення та форма-тування. Розміри діаграми змінюють, перетягуючи маркери габаритів. А вигляд змінюють за допомогою команди Формат елемента... з його контекстного меню. Під час форматування можна, зокрема, замалювати елементи деяким кольором чи текстурою. На кожну поверхню діаграми (сектор, прямокутник, стіну) можна нанести рисунок з файлу, наприклад, зображення продукції, зокрема, автомобілів, парфум тощо, чи історичних пам'ятників, що є символами міст. Можна змінити текстові підписи елементів і шрифт, яким вони виконані.
4. Створення діаграми. Діаграму можна створити командами Вставити => Об'єкт => Microsoft Graph Chart. Таблицю-зразок, яка з'явиться на екрані, слід заповнити власними даними і простежити, як автоматично змінюватиметься стовпцева діаграма-зразок. Можна такж змінювати величину стовпчика методом перетягування його вершини — дані в таблиці змінюва-
тимуться автоматично. Коли дані будуть введені, можна змінити тип діаграми за допомогою її контекстного меню.
Часто діаграми будують за допомогою програми, яка має ну Майстер діаграм. її можна запустити двома способами:
♦ натисканням на кнопку Майстер діаграм на панелі інстру-ментів;
♦ командами з меню Вставити => Діаграму. Рекомендують перед запуском майстра правильно виокремлю-
вати діапазони з даними, які треба графічно відобразити. Це зазвичай суміжні рядки чи стовпці (часто з назвами). Щоб виокремити несуміжні діапазони, потрібно натиснути на клавішу Ctrl. Під керівництвом майстра виконують чотири кроки. Крок 1: вибирають тип і вигляд діаграми (див. рис. 43).
Крок 2: задають діапазони з даними (якщо вони не були вибрані заздалегідь).
Крок 3: задають параметри (підписи, легенду, вигляд осей наявність сітки) діаграми.
Крок 4: зазначають, куди заносити діаграму (на окрему чи поточну сторінку).
Щоб перейти до наступного кроку, натискають на кнопку Далі, а щоб повернутися назад — на кнопку Назад.
Можна пропустити один чи два кроки, натискаючи відразу на кнопку Далі. Щоб завершити (часто достроково) роботу май тра діаграм і отримати діаграму, натискають на кнопку Готово.
Зміни у створеній діаграмі можна внести за допомогою кон текстного меню елементів, команди Діаграма або панелі інстру ментів з назвою Діаграма.
Щоб вставити в діаграму пропущений елемент, використо вують команди Вставити > Діаграма > Параметри діаграми
Зверніть увагу на те, що тип діаграми можна будь-коли по міняти. Для цього діаграму треба вибрати, викликати майстра діаграм, вибрати інший тип і натиснути на кнопку ГОТОВО. Вико нуючи практичну роботу, поекспериментуйте з різними типами та видами діаграм і їхніми властивостями.
Словник
Діаграма Диаграмма Chart
Майстер діаграм Мастер диаграмм Chart Wizard
Кругова Круговая Pie
Точкова Точечная XY (Scatter)
Об'ємна Обьемная 3-D Effect
Частка Частка Each Value
Категорія Категория Category
Ключі легенди Ключи легенды Legend Key
Лінії виноски Линии выноски Leader Lines
Область побудови Область построения Plot Area
Кут Угол Corner
Поверхня Поверхность Surface
Хід роботи
1. Запустіть програму ЕТ.
2. Відкрийте нову книжку і книжку, яка містить розв'язок за; «Товарний чек».
Скопіюйте таблицю «Товарний чек» на перший аркуш нової книжки. Якщо файл втрачено, побудуйте таблицю заново.
3. Виокремте діапазон з назвами предметів і діапазон з сумами, які треба заплатити.
Під час виокремлення несуміжних діапазонів користуйтеся Ctrl.
4. Запустіть Майстра діаграм і виконайте перший крок: задайте тип і вигляд діаграми. Тип: Стандартні => Кругова => Вигляд: Об'ємна => Далі.
5. Наступний (другий) крок можна пропустити, тому що джерело даних задане виокремленням. Перевірте, чи у текстовому вікні правильно описано діапазони даних: =Аркуш1!$В$2:$В$9, Аркуш1!$Е$2:$Е$9 Натисніть на кнопку Далі і виконайте наступний крок.
6. Задайте параметри діаграми.
Дайте діаграмі назву: "Купівля канцтоварів" тощо. Переконайтеся, що легенда буде праворуч. Підпис даних виберіть такий: частка. Поекспериментуйте з підписами: категорія, категорія і частка, значення. Вимкніть КЛЮЧІ легенди і ЛІНІЇ ВИНОСКИ. Натисніть на кнопку Далі.
7. Помістіть діаграму на поточній сторінці (це крок 4) і натисніть на кнопку Готово.
8. Отриману діаграму розтягніть, щоб домогтися якнайкращого розташування круга та підписів, і перемістіть її нижче від числової таблиці.
Щоб перемістити діаграму, натисніть над вибраною діаграмою на ліву клавішу миші і зачекайте, щоб вказівник став хрестоподібним — перетягніть вказівник у потрібне місце.
Сформатуйте заголовок.
Наведіть вказівник на заголовок, зачекайте мить, щоб побачити назву елемента, і викличте контекстне меню заголовка. Виконайте команду Формат заголовка: замалюйте назву жовтим кольором; задайте тип лінії рамки і її колір (зелений) з тінню. Шрифт заголовка можна не змінювати=> ОК.
10. Сформатуйте область діаграми.
Активізуйте контекстне меню області діаграми. У способі заливки виберіть текстуру до вподоби => ОК.
11. Підберіть колір для легенди.
12. Поряд побудуйте для цих же даних булькову діаграму. Збережіть книжку на диску з назвою Діаграми.
13. Відкрийте книжку, де розв'язано задачу табулювання функції і скопіюйте таблицю на другий аркуш книжки Діаграми. Назвіть аркуш Графік.
14. Виокремте два стовпці з числами з назвами Аргумент (х) і Функція (у).
15. Побудуйте графік функції.
Викличте майстра діаграм. Виберіть тип діаграми: Точкова
діаграма і вигляд: з маркерами, з'єднаними згладжувальною ЛІНІЄЮ (картинка №2) => Далі.
16. Пропустіть крок 2, якщо дані виокремлено
Впевніться, що ряди даних вибираються зі стовпців. Натисніть на кнопку Далі.
17. Задайте параметри графіка.
Введіть заголовок: Графік функції => Підпишіть осі: X — Час Y — Шлях => Заберіть лінії сітки, легенду =>Поекспери ментуйте з іншими закладками =>Далі.
18. Розмістіть діаграму на цьому ж аркуші (Графік).
Натисніть на кнопку ГОТОВО.
19. Відформатуйте графік якнайкраще.
Розтягніть зовнішню рамку діаграми і перемістіть її у зручне місце. Розмалюйте всі елементи діаграми на свій смак.
20. Побудуйте поряд графік цієї ж функції, застосувавши тип діаграми Графік.
Зверніть увагу, що для побудови графіка цього типу достатньо одного стовпця даних (у).
21. Відкрийте книжку з розв'язком задачі № 3 «Діяльність фірми в Україні».
Скопіюйте таблицю на третій аркуш. Назвіть його Гістограма.
22. Виокремте діапазон з даними про діяльність фірми про тягом трьох місяців з назвами стовпців і рядків.
23. Запустіть Майстра діаграм для побудови гістограми. Виберіть тип діаграми: гістограму і вигляд: об'ємний варіанті звичайної гістограми => Далі => Далі.
24. Виконайте крок 3. Дайте заголовки елементам діаграми. Осі не підписуйте => Заберіть лінії сітки, долучіть легенду, вим кніть підписи даних =>Далі => Готово.
25. Сформатуйте діаграму якнайкраще.
Розтягніть рамку, в якій є діаграма. Область діаграми залийте градієнтним кольором.
26. Змініть тип діаграми на об'ємний з тривимірним ефектом за допомогою контекстного меню області діаграми.
27. На одну із граней стовпця помістіть картинку з деякого bmp-файлу.
28. Клацніть на елементі Кут діаграми і поверніть площину, щоб поліпшити перегляд діаграми.
29. Клацніть на елементі Стіни і змініть формат стін, замалювавши їх жовтим кольором, або помістіть на них зображення з файлу.
30. Сформатуйте область побудови діаграми.
Повільно ведіть вказівником у рамці, доки не з'явиться такий напис: Область побудови діаграми. Клацніть лівою клавішею і розтягніть область. Клацніть правою клавішею і замалюйте її градієнтним кольором.
31. Для задачі про діяльність фірми побудуйте пелюсткову діаграму і розташуйте її на окремому аркуші Пелюсткова.
У таблиці має бути п'ять-шість рядів даних і три стовпці.
32. На наступному аркуші побудуйте таблицю зі значеннями верхньої і нижньої граней курсів валют (долара і євро) протягом шести днів тижня і побудуйте для цих даних біржову діаграму.
Назвіть аркуш Біржова.
33. Побудуйте графік функції від двох змінних z = х2 - у2.
На наступному аркуші з назвою Поверхня побудуйте таблицю значень цієї функції для значень х та у на проміжках [-2; 2] з кроком h = 0,2. Для цього перший рядок, починаючи з клітинки В1, заповніть значеннями х: -2; —1,8;...; 1,8; 2 за правилами створення арифметичної прогресії: введіть у В1 число -2. Редагувати => Заповнити => Прогресія => Арифметична => По рядках => Крок 0,2. Граничне значення 2 => ОК. Аналогічно заповніть перший стовпець значеннями у, починаючи з клітинки А2. У клітинку В2 введіть формулу =В$1^2 - $А2^2 і скопіюйте її у прямокутний діапазон B1:V22. Запустіть майстра побудови діаграм і виберіть тип діаграми Поверхня =ГОТОВО. Отриману поверхню називають сідлом або гіперболічним параболоїдом.
35. Модифікуйте таблицю і побудуйте поряд поверхню для функції z = х2 * у2.
36. Збережіть книжку на диску. Продемонструйте діаграми: кругову, булькову, точкову, графік, гістограму, пелюсткову, біржову і дві поверхні.
37. Закінчіть роботу. Закрийте вікна.
Контрольні запитання
1. Яке призначення діаграм?
2. Які є типи діаграм?
3. Що таке булькова діаграма?
4. Які є види кругової діаграми?
5. Що таке гістограма?
6. З яких елементів складається діаграма?
7. Як отримати на екрані назву елемента діаграми?
8. Які дії визначені над елементами діаграми?
9. Як розмальовувати елемент діаграми?
10. Як можна побудувати діаграму?
11. Як виокремити несуміжні діапазони даних?
12. Як працює Майстер діаграм?
13. Як вилучити діаграму з аркуша?
14. Що таке пелюсткова діаграма?
15. Що таке біржова діаграма?
16. Як підписати осі діаграми?
17. Для чого використовують точкові діаграми?
18. Як увімкнути панель інструментів Діаграма?
19. Для чого використовують стовпцеві діаграми?
20. Яка відмінність між графіком і точковою діаграмою?
21. Які є різновиди стовпцевих діаграм?
22. Як скопіювати діаграму на іншу сторінку?
23. Як розтягнути діаграму?
24. Як сформатувати заголовок діаграми?
25. Як повернути об'ємну діаграму?
26. Як змінити тип діаграми?
27. Які є типи нестандартних діаграм?
28. Як сформатувати область побудови діаграми?
29. Які осі мають діаграми?
30. Як помістити зображення на елемент діаграми?
31. Як викликати контекстне меню області побудови діаграми
32. Як побудувати поверхню?
Практична робота №5. MS Excel. Задачі апроксимації і прогнозування даних. Метод найменших квадратів. Елементи регресійного аналізу. Побу дова ліній тренду на діаграмах
Мета
Уміти використовувати математичні функції для роботи з масивами даних: MMULT (МУМНОЖ), MINVERSE (МОБР), MDETERM (МОПРЕД), TRANSPOSE (ТРАНСІ!) і статистиці ні функції для дослідження тенденцій (тренду) в даних: TREND (ТЕНДЕНЦИЯ), LINEST (ЛИНЕЙН), GROWT (РОСТ), LOGEST (ЛГРФПРИБЛ).
Задача 6 «Прогноз доходу фірми»
Протягом перших десяти місяців року доходи фірми були такими: 200 000, 220 000, 230 000, 225 000, 235 000, 225 000, 230 000, 250 000, 245 000, 280 000. Побудувати лінію тренду і спрогнозувати дохід фірми у листопаді й грудні.
План
1. Поняття про метод найменших квадратів.
2. Реалізація регресійного аналізу в ЕТ.
3. Використання функції TREND.
4. Використання функції LINEST.
5. Поняття про масиви і формули масивів.
6. Побудова ліній тренду за допомогою діаграм.
Теоретичні відомості
1. Поняття про метод найменших квадратів. Метод найменшихквадратів (МНК) застосовують для розв'язування задач про згладження експериментальних даних та апроксимацію (наближення) даних деякою нескладною аналітичною функцією з метою використання цієї функції дляпрогнозування подальших змін даних.
Такий аналіз даних також називають регресійним аналізом.
Розглянемо приклади відповідних задач. Нехай є дані про середньоденну температуру протягом перших десяти днів місяця.
Потрібно спрогнозувати температуру 11 і 12 числа, вважаючи, що тенденція щодо зміни температури стабільна.
Нехай є дані про обсяг валового доходу країни, регіону, фір-ми протягом декількох місяців. Потрібно спрогнозувати обсяги доходу в наступні місяці, вважаючи, що тренд (тенденція) стабільна, тобто немає факторів, які можуть непередбачувано змінити тенденцію.
Це приклади однофакторних задач. У першій задачі фактором є дні, які впливають на зміну даних, а у другій — місяці року. Якщо факторів є декілька, то відповідні задачі називають багатофакторними. Приклад двофакторної задачі: є дані про залежність вартості квартири від площі (це майже лінійна залежність) і від віддаленості від центру міста. Потрібно спрогнозувати вартість квартири конкретної площі в конкретному районі міста. Вартість квартири може залежати також від поверху, якості будівельних матеріалів та інших факторів.
Будь-які експериментальні дані можна однозначно апрокси-мувати лінією (функцією, рівнянням) деякого типу: прямою ліні-єю, логарифмічною, поліноміальною чи експоненціальною кри-вою за принципом найменших квадратів — так, щоб сума квадратів відхилень апроксимованих значень від експериментальних була мінімальною.
Заздалегідь складно визначити, який тип функції є оптимальним для конкретних даних, зокрема, якщо їх багато. Тому якість апроксимації оцінюють на підставі критерію, який нази-вають «критерій R-квадрат» (використовують також позначення г2). Значення г2 для різних функцій (ліній) буде різним. Апроксимація вважається тим ліпшою, чим ближче значення г2 до числа 1, та ідеальною, якщо г2=1.
Нехай у деякій однофакторній задачі кількість експериментальних даних п, значення фактора (незалежної величини, аргументу функції) утворюють масив чисел xyt x2,..., хп, значення експериментальних даних утворюють масив уг, */2,..., ул. Нехай для апроксимації вибрано і визначено функцію f(x).

2. Реалізація регресійного аналізу в ЕТ. Розглянемо найпростіший спосіб прогнозування даних. Достатньо виокремити діапазон з експериментальними даними У і перетягнути маркер копіювання на k клітинок (вниз) — отримаємо лінійний прогноз для точок хп+1> xn+2> •••» xn+k • Якщо перетягування виконати правою клавішею миші, то з контекстного меню можна вибрати тип апроксимації: лінійною тхЛ-Ь чи експоненціальною bm функцією (залежно від тенденцій у даних). Недоліками такого способу є припущення, що фактором X є масив чисел 1, 2, 3,., а також нереагування прогнозованих значень на зміни в експе риментальних даних.
Інший спосіб розв'язування задачі — це застосування інст румента Регресії, який запускають командою Сервіс => Аналіз даних... =>Регресії => ОК. Він забезпечує лінійну апроксимацію даних і повертає статистичну інформацію, що дає змогу оцінити якість апроксимації.
Головним способом розв'язування задачі лінійної апрок симації і прогнозування даних є використання статистичної функції TREND(діапазон1; діапазон2; діапазонЗ). Діапазон має містити експериментальні дані уґ Діапазон2 — значення,х ДіапазонЗ має містити точки для прогнозу хп+1, хпі_2, • ••, хп^л Функціюможна використовувати з двома аргументами або трьома. У першому випадку розв'язують задачу апроксимації експериментальних даних прямою лінією, а в іншому випадку — задачу прогнозування даних.
3. Використання функції TREND. Розглянемо алгоритм розв'язування задачі апроксимації даних прямою лінією, який реалізується статистичною функцією TREND.
1. Утворити вертикальний діапазон з хі який назвати X.
Діапазон для задачі 6 має містити числа 1, 2,..., 10. Щоб діа-пазон назвати як X, треба його виокремити і виконати команди Вставити > Ім'я > Присвоїти > Введіть X > Додати > ОК.
2. Утворити вертикальний діапазон з у, кому надати ім'я Y.
3. Поряд вибрати порожній вертикальний діапазон з п клітинок.
4. У рядок формул ввести формулу =TREND(Y;X).
5. Натиснути на комбінацію клавіш Shift--Ctrl-Enter — результати f(xt) заповнять порожній діапазон.
Розглянемо алгоритм прогнозування даних для значень фактора хпМ,хп+2,...,х,н+h
6. Утворити вертикальний діапазон із зазначених значень фактора (тут 11, 12) під діапазоном X і назвати його Z.
7. Поряд вибрати порожній вертикальний діапазон з k клітинок.
8. У рядок формул ввести формулу =TREND(Y;X;Z).
10. Натиснути на комбінацію клавіш Shift+Ctrl+Enter —
результат-прогноз fх., і=/г+1,..., /k, заповнить порожній діапазон.
Тепер можна виконати додаткові обчислення для визна-чення значень т, b та г2 за формулами, які наведені вище.
Якщо виявиться, що апроксимацію виконано невдало (тен-
денція зміни даних є далекою від лінійної, г2<0,8), то слід ви-брати іншу функцію, наприклад GROWTH(), яка здійснює експо-ненціальну апроксимацію, або скористатися графічним способом розв'язування задачі.
4. Використання функції LINEST. Функція LINEST(Y; X;
True; True) повертає масив, перший рядок якого — це значення m та b,другий — це стандартні похибки цих двох значень відповідно, третій рядок містить значення r2 і стандартну похибку для функції, четвертий рядок містить дані, які використовуються в теорії F-статистики. Цікавою особливістю функції є те що її можна використати для лінійного багатофакторного регресійного аналізу. Для експоненціального аналізу є функція LOGEST().
5. Поняття про масиви і формули масивів. Одновимірним масивом чисел називають послідовність чисел, взятих у фігурні дужки, наприклад {1; 1,5; 4,2}. Двовимірний масив містить набори чисел, які розмежовані символом двокрапка (якщо числа відокремлюються крапкою з комою і кома є десятковим розділю-вачем) або крапкою з комою (якщо розділювачами є кома та рапка відповідно), наприклад {1; 1,5; 4,2:1; 1,5; 4,2}. Один набір чисел відповідає рядку чисел у зображенні масиву у вигляді матриці. Діапазон з числами можна трактувати як масив чисел (матрицю).
Над матрицями-масивами визначені операції додавання віднімання, множення на число, а також такі функції: множення матриці на матрицю — ММULТ(матриця1; матри ця2), транспонування — TRANSPOSE(Macив чи діапазон), обчислення оберненої матриці — MINVERSE(Macив) та детермі нанта (визначника) матриці — MDЕТЕКМ(матриця).
Зауважимо, що діапазони можна перемножувати, але це не тотожно добуткові масивів-матриць. Добуток двох діапазонів -це діапазон з покомпонентно перемноженими елементами, що можна використати для розв'язування багатьох задач. Напри клад, вартість всіх товарів (одне число) у задачі про товарний чек можна визначити за допомогою такої формули: {=SUM(Kiль. кість* Ціна)}.
Формулу для дій з масивами чи діапазонами називають формулою масиву. Перед виконанням дій з масивами потрібно вибрати порожній діапазон клітинок, де міститиметься результат обчислення формули-масиву. Особливість дій користувача така: після набору формули у рядку формул її вводять у ЕТ не простим натисканням клавіші Enter, а комбінацією клавіш Shift-fCtrl + -Enter. Формула масиву буде записана у фігурних дужка х автоматично (їх не набирають). Формули масивів слід застосу вати в цій роботі для обчислення значень т, b і г2.
6. Побудова ліній тренду за допомогою діаграм. Лінії тренду призначені для графічного відображення тенденції даних і прог нозування їх подальших змін. Використовуючи регресійний аналіз, можна продовжити лінію тренду в діаграмі за межі ре альних даних для передбачення майбутніх значень.
Лінії тренду можна додати до рядів даних, зображених на ненормованих плоских діаграмах з областями, лінійних діагра мах, гістограмах, графіках, біржових, точкових і булькових діаграмах. Нееможливо додати лінії тренду до рядів даних на об'ємних, нормованих, пелюсткових, кругових і кільцевих діа грамах.
Є шість різних типів ліній тренду, які можна додати до діаграми. Тип лінії тренду потрібно вибирати, виходячи з типу даних (візуально аналізуючи тенденції в даних).
1. Лінійна апроксимація — це пряма лінія, яка наближено описує сукупність даних. її застосовують у найпростіших випад ках, коли дані розташовані близько до прямої.
2. Логарифмічну апроксимацію використовують для опису величини, яка спочатку швидко зростає або зменшується, а потім поступово стабілізується. Для логарифмічної апроксимації мож на використовувати як від'ємні, так і додатні значення даних.
3. Поліноміальну апроксимацію використовують для опису величин, які то плавно зростають, то спадають, а також для аналізу великої сукупності даних. Степінь полінома (до шостого) визначають кількістю екстремумів (максимумів і мінімумів) серед даних. Поліном другого степеня може описати лише один максимум або мінімум. Поліном третього степеня може мати два mекстремуми і т. д.
4. Степеневу апроксимацію використовують для опису ве личини, що монотонно зростає або монотонно спадає, наприклад, відстані, яку проходить автомобіль під час розгону.
5. Експоненційну апроксимацію використовують у тому випадку, якщо швидкість зміни даних безперервно зростає, наприклад, у задачах розмноження вірусів. Неможливо застосувати степеневу й експоненційну апроксимацію, якщо дані містять нульові або від'ємні значення.
6.. Є ще метод апроксимації даних, який називають змінним середнім (лінійною фільтрацією, рос. скользящее среднее). Лінія тренду будується за певною кількістю точок (ця кількість визнаначається параметром Точки). Метод застосовують, коли точок є,багато і вони дуже розкидані. Дані усереднюють попарно чи інакше й одержані середні значення використовують для апроксимаціїї. Якщо значення параметра Точки є 2, першу точку кривої визначають як середнє значення перших двох даних, другу точку як -середнє значення другого і третього даного і т. д. Розглянемо алгоритм додавання лінії тренду до діаграми.
1. Побудувати діаграму для ряду експериментальних даних.
2. Клацнути правою клавішею на маркері ряду даних, для яких треба побудувати лінію тренду — отримаємо контекстне меню ряду даних.
3. Виконати команду Додати лінію тренду. 4. На закладці Тип вибрати тип лінії тренду.
5. На закладці Параметри задати назву кривої (можна не задавати), довжину відрізка (в одиницях зміни аргументу) прог-нозу, координату точки перетину з віссю У (можна не задавати),
зобразити рівняння регресії на діаграмі, розташувати на діаграмі значення г2 (R^2).
6. ОК.
ХІД РОБОТИ
1. Запустіть ЕТ і відкрийте нову книжку.
2. Уведіть у три діапазони масиви чисел у вигляді матриць: масив А і В розмірності три на три (по 9 елементів) і масив-стовпець D з трьох елементів.
Надайте діапазонам імена А, В і D.
3. Обчисліть 2*А.
4. Обчисліть добуток масивів-матриць А*В.
5. Обчисліть суму масивів-матриць А+В.
6. Обчисліть добуток діапазонів D*D. Результат — діапазон з квадратами даних з D.
7. Обчисліть детермінант матриці А.
Якщо детермінант дорівнює нулю, змініть числа в матриці А,
8. Розв'яжіть систему лінійних алгебраїчних рівнянь АХ= D, Метод розв'язування Х= А"1*D, де А1 — обернена матриця.
9. Перейдіть на новий аркуш для розв'язування задачі № 6 У першому рядку введіть заголовки стовпців: Місяці, X, У, Апроксимація.
10. Уведіть у другий рядок список назв місяців шляхом авто заповнення рядка і транспонуйте рядок з елементами списку в стовпець..
Виберіть стовпець і застосуйте формулу {=TRANSPOSE(A2:K2)
11. Виконайте алгоритм використання функції TREND().
12. Побудуйте плоску стовпцеву діаграму для експери ментальних даних з графіком лінії тренду.
Виберіть спочатку діапазон, що містить експериментальні (Y), апроксимовані та прогнозовані дані (Апроксимація). Запустіть Майстра побудови діаграм. На першому кроці виберіть на закладці нестандартних діаграм тип Графік | Гістограма, що дасть змогу накласти графік лінії тренду на діаграму.
13. Обчисліть значення m і b.
Для обчислення сум застосуйте формули масивів на зразок {=SUM(niana3OHl* діапазон2)} і Ctrl+Shift+Enter.
14. Обчисліть значення r2.
15. Застосуйте функцію LINEST().
Аргументи функції описані в теоретичних відомостях. Пере вірте, чи збігаються ваші результати щодо значень m, b r2,. зі значеннями, які дає ця функція.
16. Скопіюйте вхідні дані задачі № 6 на третій аркуш.
17. Дослідіть графічні способи прогнозування за допомогою ліній тренду різних типів. Нанесіть на аркуш шість діаграм з лініями тренду.
Виберіть діапазон чисел Y і побудуйте просту стовпчикову діа граму (або графік з маркерами тощо). Застосуйте описаний в теоретичних відомостях алгоритм нанесення ліній тренду а відповідними параметрами дляпрогнозу на дві одиниці вперед і виведення рівнянь регресії та значення r 2.
18. Зробіть висновок про те, який тип апроксимації є най ліпшим.
19. Який прогноз обсягів доходу фірми у листопаді та грудні?
20. Продемонструйте три аркуші та закінчіть роботу.
Контрольні запитання
1. Що таке МНК і яке його призначення?
2. У чому полягає суть задачі апроксимації даних?
3. У чому полягає суть задачі прогнозування даних?
4. Що таке регресійний аналіз?
5. Що таке однофакторний аналіз? Наведіть приклад задачі.
6. Що таке багатофакторний аналіз? Наведіть приклад задачі.
7. Які види ліній використовують для апроксимації даних?
8. Як оцінюють якість апроксимації?
9. Як найпростіше отримати лінійний прогноз даних?
10. Яке призначення функції TREND()?
11. Який алгоритм використання функції TREND()?
12. Яке призначення функції GROWTH()?
13. Яке призначення функції LINEST()?
14. Яке призначення функції LOGEST()?
15. Що таке масив чисел в ЕТ?
16. Які дії можна виконувати над масивами?
17. Які є функції для дій з масивами?
18. Що таке формула-масив?
19. Яке призначення акорду Shift+Ctrl+Enter?
20. Яке призначення ліній тренду?
21. Які лінії тренду можна нанести на діаграму?
22. На які діаграми можна нанести лінії тренду?
23. Як нанести лінію тренду на діаграму?
24. Що таке метод «змінного середнього»?
25. Що означає оцінка г2?
Практична робота №6. MS Excel. Організація розгалужень та ітерацій. Метод добирання параметра. Задача «Нарахування зарплатні». Задача «Розв'язування нелінійного рівняння»
Мета
Уміти використовувати логічну функцію ЯКЩО (ЕСЛИ, IF) та абсолютні адреси клітинок для розв'язування типових економічних і математичних задач.
Задача 7 «Нарахування зарплатні»
У відомості нарахування зарплатні є прізвища шести-восьми працівників, які мають один із трьох кваліфікаційних розрядів: 1, 2, 3. Денна тарифна ставка залежить від розряду так (в у.о.):
ґ 12, якщо розряд = 3; Ставка = < 10, якщо розряд = 2;
V 8, якщо розряд = 1.
Протягом місяця працівники зайняті різну кількість днів Треба ввести кількість відпрацьованих днів і нарахувати зарплатню працівникам, якщо відрахування (податки тощо) становлять 13% від нарахувань. Скласти бухгалтерську відо мість (див. рис. 44).
Задача 8 «Розв'язування нелінійного рівняння»
Дано нелінійне рівняння 2пх-п = sinnx, де п — номер варіанта. Розв'язати рівняння методом простих ітерацій (див. рис. 45) і методом добирання параметра.
План
1. Абсолютна і змішана адреси.
2. Логічні функції.
3. Дати.
4. Метод добирання параметра.
5. Метод простих ітерацій.
Теоретичні відомості
1. Абсолютна і змішана адреси. Розглянемо поняття абсолют ної і змішаної адрес клітинки у формулі. Абсолютною називають адресу, в якій є два символи $: один перед назвою стовпця, другий — перед номером рядка, наприклад $Е$3. Змішана адреса місти ть, лише один символ $. Правило: частина адреси після символу $ не модифікується під час копіювання формули.
Абсолютні адреси слугують, зокрема, для посилання на клітинки, які містять константи, що є у формулах. Такою ют стантою є, наприклад, відсотки (12% =0,12) річних у задачі2. Якщо для задачі 2 число 0,12 занести в клітинку ЕЗ, тов клітинку СЗ можна ввести формулу = ВЗ*$Е$3.
2. Логічні функції. Розгалуження в ЕТ реалізовують допомогою функції ЯКЩО (ЕСЛИ, IF), яка використовується у формулах і має таку структуру:
ЯКЩО(<логічний вираз>; <вираз 1>; <вираз 2>).
Логічний вираз — це форма запису умови: простої або складеної.
Якщо умова істинна, то функція набуває значення першого виразу, інакше — другого.
Вираз 1 чи вираз 2 також може бути функцією ЯКЩО —так утворюють вкладені розгалуження. Часто виразом 1 чи виразом 2 є лише адреса клітинки, яка містить деяке значення або конкретне число.
Прості умови записують так, як в алгоритмічних мовах —за допомогою операцій порівняння =, >, <, <=, > =, <>, визначених над виразами, наприклад, 7>5, А5<=20 тощо.
Складені умови записують за допомогою логічних функцій||(умова1>;<умова2>;...) та АБО(<умова1>;<умова2>;...). Функція І (И, AND) істинна, якщо всі умови в списку істинні. Функція АБО (ИЛИ, OR) істинна, якщо хоч би одна умова в вписку її аргументів істинна.
Наприклад, функція ЯКЩО(АБО(5>7; 5<7); 5; 7) набуває значення 5, а функція ЯКЩО(І (5>7; 5<7); 5; 7) — значення 7. Якщо користувач не пам'ятає вигляду функції, він може вста вити її у вираз за допомогою майстра функцій, який викли-кають командою Вставити => Функція. У цьому разі потрібно ви-брати назву функції із запропонованого списку (крок 1) і запов-нити поля значеннями параметрів (крок 2).
Працюючи в Excel, потрібно користуватися російськими (ЕС-ЛИ, И, ИЛИ) або англійськими (IF, AND, OR) назвами функцій. 3. Дати. В економічних чи бухгалтерських задачах дати тра-I и миються доволі часто. Дати в ЕТ чисто умовно зачисляють до даних типу дата. Наспраді дати зберігаються в ЕТ як цілі числа і лише відображаються на екрані в тому чи іншому форматі, наприклад: 12 січня 2006 р. чи 12.01.2006, чи 2006-01-12, чи 88729. За точку відліку дат взято 1 січня 1900 року. Будь-яка дата еквівалентна цілому числу, що дорівнює кількості днів, які минули від точки відліку (38729 для 12 січня 2006 p.). Це дає змогу виконувати над датами такі операції: віднімати дати для визначення проміжку днів між двома датами, додавати чи від-німати від дат ціле число.
Можна застосовувати функції опрацювання дат з метою визначення окремих компонент дати: поточного номера дня в тижні (WEEKDAY), в місяці (DAY), номера місяця в році (MONTH), року (YEAR), поточної дати (TODAY) тощо. Ці функції потрібно вставляти у вирази командами Вставити => Функція => Дати і час. Деякі з цих функцій мають параметри, дія яких описується у відповідному діалоговому вікні.
Час задається годиною, хвилиною, секундою. Йому від-даповідає десяткове число від 0 до 1, що відображає частину доби.
Щоб відобразити числові значення дати і часу в клітинці потрібно встановити формат клітинки загальний.
4. Метод добирання параметра. Метод добирання параметри призначений для розв'язування нелінійного рівняння f(x)=е, Суть методу полягає в тому, щоб автоматично визначити (а деякою точністю) таке значення параметра х, для якого функція f(x) одержує потрібне значення с
Цей засіб має важливе значення для розв'язування задач зворотного економічного аналізу. Наприклад такої: скільки треба купити одиниць деякого товару (це є параметр), щоб вклас тися в заплановану суму (це функція).
Розглянемо задачу: встановити тарифну ставку (це пара метр) дванадцятьом працівникам, щоб вкластися в запланований обсяг зарплатні (це функція) 1000 грн.
Модель задачі. Нехай А1 — адреса клітинки, що міститиме відповідь — значення параметра-ставки, a f(Al) — задана функ ція (мета дослідження), наприклад, зарплатня(А1) = 12*А1 Складаємо рівняння, яке є математичною моделлю задачі 12*А1 - 1000.
Хоча задача дуже проста, застосуємо для її розв'язування метод підбору параметра, який полягає в тому, що програма сама
має підібрати значення А1, щоб задовольнити будь-яке рівняння
Алгоритм дій користувача такий.
1. У будь-яку клітинку (але не в А1) треба занести формулу = f(Al). У нашому випадку формула така: = 12*А1.
2. Вибрати цю клітинку і виконати команду Сервіс => Підбір параметра. Отримаємо діалогове вікно Підбір параметра.
3. Заповнити три поля: а) зазначити адресу формули (вони буде вказана автоматично, якщо клітинка з формулою була вибрана перед цим); б) бажане значення формули, тобто с (у нашому випадку 1000); в) адресу параметра — А1.
4. Натиснути на ОК і у клітинці А1 отримати результат. Другий спосіб полягає у використанні можливостей програми Solver («Пошук розв'язку»), що додається до Excel. Вона дає змогу розв'язувати задачі з багатьма параметрами і з обмежсн нями. Наприклад, такі: скільки треба купити одиниць двох чи трьох найменувань товарів (це параметри), щоб вкластися в заплановану суму (це функція) і щоб кількості товарів не пере вищували деяких величин (це обмеження у вигляді нерівностей, див. роботу № 24).
5. Метод простих ітерацій. Продовжимо вивчати застосу вання електронних таблиць для розв'язування типових матема тичних задач. Розглянемо ще два способи розв'язування нелінійІ ного рівняння: 1) метод простих ітерацій з побудовою таблиці; 2) метод простих ітерацій з використанням двох клітинок.
Розглянемо метод простих ітерацій. Щоб нелінійне рівняння f(х) = с можна було розв'язати методом простих ітерацій, його зводятьдо вигляду х = z(x) так, щоб виконувалась нерівність: z(х)| < 1. За цієї умови метод простих ітерацій збігається, тобто
Ідає правильний розв'язок. Наприклад, рівняння 2пх~п = sinnx спочатку треба звести до такого вигляду: х = (sinx + п)/2п.
Метод простої ітерації реалізують за допомогою рекурентної формули так:
xl+l = (sinx + п)/2п.
дг х — будь-яке початкове наближення, і=0, 1, 2,..., а замість п треба підставити значення свого варіанта. Домовимося, що коли t=8, то значення xі (тобто х8) вважатимемо розв'язком рівняння. Розглянемо реалізацію рекурентної формули в ЕТ. Нехай n= 1, а в клітинку А6 введено будь-яке початкове наближення, наприклад 2. Тоді наступне наближення отримаємо в клітинці B6, ввівши туди формулу =(Sin(А6)+1)/2. Це значення приймаємо за початкове для наступної ітерації: в А7 заносимо значення В6. У клітинці В7 отримуємо наступне наближення і т.д. У клітинці В1З буде останнє (восьме) наближення, яке і прий-маємо за розв'язок.
Другий спосіб полягає у використанні властивості ЕТ автоматичного багаторазового переобчислення, якщо ввімкнений режим ітерацій у діалоговому вікні Параметри. Тут для розв'язування задачі достатньо двох клітинок (див. рис. 45, рядок 17). Цей спосіб розглянемо під час виконання роботи.
Словник
Підбір параметра Подбор параметра Goal Seak
Пошук розв'язку Поиск решения Solver
Дата Дата Date
Якщо/і/або Если/и/или If/ And/Or
Захист Защита Protection
Функція Функция Function
Ітерації Итерации Iterations
Клітинка-ціль Целевая ячейка Targer Cell
Обмеження Ограничения Constraints
Сторінка/Книжка Лист/Книга Sheet/Book
СЬОГОДНІ СЕГОДНЯ TODAY
Хід роботи
1. Запустіть програму ЕТ, створіть нову книжку, назвіть аркуш Зарплатня і задайте режим відображення формул

3. Розгляньте умову задачі 7 і введіть вхідні дані для шести працівників (див. рис. 44, але не копіюйте з нього дані).
У таблиці вводьте дані лише в стовпці А, В, С, D, пам'ятаючи, що є лише три розряди (1, 2, 3) і днів у місяці є не більше ніж 31.
АдресиДані
А1 Відомість нарахування зарплатні від
Е1 =СЕГОДНЯ() або =TODAY()
Примітка: введіть дату і виберіть для неї формат
В2 Тарифні ставки: D2 8
Е2 10
F2 12
G2 0,13
A3 Номер
В3 Прізвище СЗ Розряд D3 Днів
ЕЗ Тариф
F3 Нараховано
G3 Відрахування
НЗ Видати
А4 1
В4 <Конкретне прізвище 1>
С4 <конкретний розряд: 1, 2 або 3>
D4 <кількість відпрацьованих днів>
А5 2
B5 <конкретне прізвище>
С5 <конкретний розряд>
D5 <кількість відпрацьованих днів>
і т.д. (введіть дані для шести працівників)
4. Уведіть формули розв'язування задачі:
Е4 = ЕСЛИ (C4=1;$D$2; ЕСЛИ (С4=2; $Е$2; $F$2))
F4 = D4 * Е4
G4 = F4 * $G$2
Н4 = F4 - G4
5. Скопіюйте формули в усю робочу таблицю.
6. Уведіть формули для обчислення балансу:
D10 Всього
F10 <обчисліть суму в стовпці F>
G10 <обчисліть суму в стовпці G>
Н10 <обчисліть суму в стовпці Н>
Н12 =G10+H10
Н13 = ЕСЛИ (Н12=F10;"ОК";"Помилка")
7.Скасуйте режим відображення формул.
Скільки всього нараховано зарплатні? Чи збігається баланс? Скільки повинен отримати другий працівник?
8. Скопіюйте таблицю на другий аркуш.
9. На аркуші 2 підвищіть денну оплату праці (тарифні ставки) всім категоріям на три одиниці і зменшіть відрахування на 2%.
Скільки всього нараховано зарплатні тепер? Чи збігається баланс? Скільки тепер повинен отримати другий працівник?
10. Зніміть захист з даних у стовпці Днів. Захистіть решту таблиці від несанкціонованих змін, задавши пароль: money. Виберіть діапазон даних зі стовпця D і ліквідуйте захист його клітинок командами Формат > КЛІТИНКИ > Захист >Вимкніть перемикач захисту клітинки. Решту клітинок захистіть командою Сервіс > Захист > Захистити > Лист. Пам'ятайте: коли вводять пароль, на екрані відображаються зірочки. Переконайтеся, що в стовпець С внести зміни не можна. Внесіть зміни в стовпець D: другий робітник відпрацював 28 днів. Скільки він заробив?
11. Перейдіть на аркуш 3. Додайте до таблиці три стовпці: Початок, Стаж, Премія. У стовпець Початок введіть дати початку трудової діяльності працівників.
12. У наступному стовпці Стаж обчисліть стаж працівників (у
Роках).
Від дати в $Е$2 потрібно відняти дати зі стовпця Початок і результат поділити на 365. Формат клітинки задати як числовий загальний.
13. Нарахуйте премію працівникам від нарахованої суми 10%, якщо стаж до 5 років, і 25%, якщо стаж більший.
14. Перейдіть на наступний аркуш для розв'язування задачі 8
15. Запишіть своє рівняння у вигляді O=f(x) і розв'яжіть його методом підбору параметра.
Введіть у А1 деяке близьке до х число або будь-яке число.У клітинку А2 введіть =f(Al), тобто формулу = 2*n*Al-n- sin(n*Al), де замість n вводьте номер варіанта. Виконайте команди Сервіс > Підбір параметра. Заповніть в отриманому діалоговому вікні три поля так: А2, 0, А1 B5 >Ок. Відповідь буде в клітинці А1

16. На наступному аркуші розв'яжіть нелінійне рівнянн методом простих ітерацій.
Введіть заголовок таблиці і назви стовпців так (рис. 45):
А1 Розв'язування нелінійного рівняння
А2 <введіть вигляд свого рівняння>
A3 методом простої ітерації
А5 Попередня Примітка: маємо на увазі ітерації
В5 Наступна С5 Похибка
16. Уведіть формули розв'язування задачі 8:
Аб <введіть будь-яке число>
В6 <введіть свою формулу методу простої ітерації>
С6 =abs(B6-A6)
А7 =В6
Більше нічого вводити не треба.
18. Скопіюйте формули з А7, В6, С6 вниз до 13-го рядка.
Скільки буде виконано ітерацій?
19. Скасуйте режим відображення формул і в клітинці В13 отримаєте результат.
Який результат і яка різниця між двома останніми наближеними значеннями? У скільки разів зменшується ця різниця (похибка) після кожної ітерації?
20. Сформатуйте числові дані, щоб було п'ять знаків після десяткової крапки.
21. Скопіюйте таблицю на наступний аркуш і переробіть її так, щоб розв'язати цю ж задачу, користуючись іменами m діапазонів.
Замість назви стовпця Попередня введіть назву х, замість назви Наступна - z. Відповідно змініть формули в клітинках В6 і С6. Виконайте додатково ще дві ітерації. Яка відповідь тепер?
22. На наступному аркуші розв'яжіть нелінійне рівняння засобом Solver (Пошук розв'язку).
Сервіс > Пошук розв'язку. Заповніть діалогове вікно (рис. 46): клітинка-ціль (це А2 чи інша), куди заздалегідь було введено формулу =f(Al), цільове значення — 0, змінюючи клітинку А1. Обмежень немає. Виконати.
23. Розв'яжіть задачу 8 у двох клітинках.
Задайте режим ітерації: Сервіс >Параметри > Обчислення > Ітерації > ОК. У клітинку А17 введіть будь-яке початкове наближення. У клітинку В17 введіть праву частину формули методу простої ітерації як вираз від А17, наприклад, =(sin(A17)+l)/2. У клітинку А17 введіть цю ж формулу як вираз від В17, тобто =(sin(B17)+l)/2. Який одержали результат?
24. Збережіть книжку на диску.
25. Продемонструйте сім аркушів і закінчіть роботу.
Контрольні запитання
1. Як реалізуються розгалуження в ЕТ?
2. Яке значення функції ЯКЩО(1+3>5-2; 1; 2)?
3. Як обчислити суму чисел у стовпці?
4. Який загальний вигляд має функція ЯКЩО?
5. Як скопіювати формулу? Яке значення функції ЯКЩО(5=5; МІЩ4; 6); МАКС(4; 6))?
6. Які ви знаєте логічні функції?
7. Яке значення функції I(2=2; 3=3; 3<4)?
8. Яке значення функції ЯКЩО(2>1; 10-5; 20/2)?
9. Яке призначення кнопки Автосума?
10. Що таке абсолютна і змішана адреси клітинки?
11. Як скопіювати таблицю на іншу сторінку?
12. Яка відмінність між відносними і абсолютними адресами?
13. Яке значення функції ЯКЩО(1=2; 15; ЯКЩО(ТRUЕ;20;25)
14. Яке значення функції АБО(1=2; 3=3; 4=5; 0,5>sin(250))?
15. Як ввести дату в клітинку?
16. Який загальний вигляд має логічна функція І?
17. Який розділювач можна використовувати у списках аргументів функції?
18. Як визначити, скільки днів минуло від вашого дня народження
19. Як вставити стовпець у таблицю? Яке значення ЯКЩО(5>2) ЯКЩО(5<3; 2; 4); 8)?
20. Як заповнити стовпець значеннями арифметичної прогресії
21. Як задати чи скасувати режим відображення формул?
22. Який загальний вигляд має логічна функція АБО?
23. Як вилучити рядок з таблиці?
24. Як розграфити таблицю? Яке значення функції ЯКЩО(АБО(3<5; 4<8); 8; 12)?
25. Яку стандартну функцію заміняє кнопка Автосума?
26. Як виокремити несуміжні діапазони клітинок?
27. У чому полягає метод підбору параметра?
28. Як перейти на іншу сторінку? Як перейменувати сторінку?
29. Як очистити весь стовпець? Яке значення ЯКЩО(8>2; СУММ(2; 8); МАКС(2;8))?
30. Які задачі можна розв'язати методом підбору параметра?
31. Які є функції для роботи з датами?
32. Яка відмінність між логічними функціями І та АБО?
33. Що таке засіб «Пошук розв'язку» (Solver)?
34. Яке значення функції ЯКЩО(2>1; ЯКЩО(1>2; 5; 8); 6)?
35. Які є способи розв'язування нелінійного рівняння?
Практична робота №7. MS Excel. Фінансові функції
Мета
Вміти використовувати фінансові функції для налізу вигідності інвестицій в бізнес.
План.
1. Функція для визначення майбутньої вартості теперішніх інвестицій.
2. Функції для визначення виплат для погашення позики.
3. Функції для визначення теперішньої вартостмайбутніх інвестицій.
4. Функції користувача. Створення модуля.
ТЕОРЕТИЧНІ ВІДОМОСТІ.
Фінансові функції використовують для розв’язування задач планування фінансової діяльності, визначення прибутків, аналізу вигідності капіталовкладень, кредитно - інвестиційної політики тощо. Інвестицією називають вкладання грошей у деякий бізнес на певних умовах. Позика у банку називається кредитом, а внесок на рахунок в банку – депозитом. Надходження грошей від деякого бізнесу називають рентою. Розглянемо основні параметри фінансових функцій і їхні скорочені назви:
· процентна ставка (ПС) виражається у відсотках і може бути добовою, місячною, річною тощо;
· кількість періодів (КП) кожний тривалістю доба, місяць, рік;
· періодична виплата (ПВ) – сума, яку виплачує клієнт що періоду (це від’ємне число), або сума, яку отримує клієнт що періоду (це додатне число);
· сума внеску (СВ) – сума інвестицій, капіталовкладення, початкового внеску (це від’ємне число або нуль);
· тип операції (Т) – число 0, якщо виплата здійснюється наприкінці кожного періоду, і число 1, якщо на початку.
Розрізняють кредитну і депозитну процентні ставки. Кредитна ставка є вищою ніж депозитна. Процентна ставка повинна бути узгоджена з тривалістю періоду, наприклад, річна ставка 24% відповідає місячній ставці 2%. У цій роботі вважатимемо що місячна депозитна ставка – 1% (1% = 0,01), а кредитна – 2%.
1. Функція для визначення майбутньої вартості теперішніх інвестицій. Функція має вигляд БС (ПС; КП;ПВ;СВ;Т). Англійська назва функції FV/
Якщо параметр має значення 0, то його можна не зазначати. Якщо параметр пропускають в середині списку параметрів, то два розділювачі (у цьому випадку;) мають бути поряд.
Задача 1. Інвестор вкладає в бізнес 5000 грн. (чи відкриває на цю суму рахунок в банку) на умовах 1% ставки прибутку щомісяця. Яка вартість інвестицій через 12 місяців?
Розв’язок задачі дає така формула:
= БС(1%; 12;; - 5000) або БС (0,01; 12;; - 5000)
Відповідь: 5634,13 грн.
Зауваження. Вважатимемо, що десяткові числа записуються з використанням коми, а не крапки.
Задача 2. Клієнт відкриває рахунок у банку на умовах 1% ставки прибутку щомісяця, кладе на рахунок 5000 грн. і планує на початку кожного місяця забирати з рахунку 200 грн. Яка сума буде на рахунку через 12 місяців
=БС(1%; 12; 200; -5000; 1)
Відповідь: 3 072,26 грн.
Задача 3. Умова та сама, але клієнт планує не забирати, а докладати по 200 грн на початку кожного місяця.
=БС(1%; 12; -200; -5000; 1)
Відповідь: 8 195,99 грн.
2. Функції для визначення виплат для погашення позики.
Введемо нові терміни і їхні скорочені назви:
номер періоду (НП);
сума позики (СП);
кінцеве значення позики (КЗ).
Функція ПЛТ (англ. РМТ) призначена для визначення суміш періодичних виплат для погашення боргу і має вигляд ПЛТ (ПС;1 КП; СП; КЗ; Т). Така виплата складається з двох частин, які обчислюють за допомогою двох функцій ПРПЛТ і ОСПЛТ (англ, ІРМТ та РРМТ), а саме:
а) виплата за процентами ПРПЛТ(ПС; НП; КП; СП; КЗ; Т);
б) основна виплата ОСПЛТ(ПС; НП; КП; СП; КЗ; Т).
Виплата за процентами щоперіоду зменшується, а основна І виплата щоперіоду зростає, їхня сума постійна і дорівнює ПЛТ.
Задача 4. Бізнесмен взяв у банку кредит на суму 5000 грн 1 терміном на 12 місяців за умови щомісячного погашення позики і місячної ставки кредиту 2%. Визначити величину щомісячнії.\ виплат і її складові наприкінці першого місяця.
= ПЛТ(2%; 12; 5000). Відповідь: -472,80 грн.
= ПРПЛТ(2%; 1; 12; 5000). Відповідь: -100,00 грн.
= ОСПЛТ(2%; 1; 12; 5000). Відповідь: -372,80 грн.
Задача 5. Побудувати таблицю значень двох складових
ПРГІЛТ і ОСПЛТ щомісячних виплат наприкінці кожного ] місяця за кредит (5000 грн, 2%) протягом року. Для шести місяців розв'язок показано на рис. 45,а.
Розглянемо функцію КПЕР (англ. назва NPER), яка обчис лює кількість періодів, потрібних для погашення суми позики, наданої під деяку процентну ставку за умови заздалегідь заданої суми періодичних виплат: КПЕР(ПС; ПВ; СП; КЗ; Т).
Задача 6. Позику 5000 грн беруть за умови повертання на прикінці кожного місяця 500 грн і процентної ставки 2%. Скільки місяців потрібно для повертання позики?
=КПЕР(2%; -500; 5000)
Відповідь: 11,27 місяця.

Рис. 45,а. Зразок розв'язування задач 1-5.
Функція СТАВКА(КП; ПВ; СП; КЗ; Т; початкове наближення) визначає вигідність надання позики, тобто реальну процентну < пківку від надання позики на певну суму за умови фіксованих періо-ііічішх виплат протягом деякої кількості періодів. Тут потрібно • і;іти деяке початкове наближення до шуканої процентної ставки, ті приклад 0,1 (10%). (Англ. RATE).
Задача 7. Бізнесмен звертається до банку за позикою (кредитом) на суму 5000 грн на 12 місяців за умови періодичних tut плат 450 грн наприкінці кожного місяця протягом року. Назначити процентну ставку позики. =СТАВКА(12; -450; 5000; 0; 0; 0,1)
Відповідь: 1%. Така позика для банку є невигідною, якщо місячна депозитна процентна ставка 1%. Банк позики не надасть.
3. Функції для визначення теперішньої вартості майбутніх інвестицій. Розглянемо функції для визначення вигідності інвестицій (капіталовкладень) у деякий бізнес.
Депозитна процентна ставка (ДПС) — це ставка, яку банк шшлачує за вклади клієнтів.
Функція ІІС(ДПС; КП; рента за один період; рента в кінці ифміну; Т) обчислює сьогоднішню вартість низки майбутніх над-\ оджень (ренти) від бізнесу (англ. PV).
Для обчислення сьогоднішньої вартості майбутньої ренти пмкористовується принцип дисконтування — приведення суми ропти (доходу) за деякий термін до її вартості в цей момент часу, враховується депозитна процентна ставка, оскільки вважається, що вже перше надходження стає депозитом у банку. Дисконту-ммпня дає відповідь на запитання: чи варто вкладати гроші в ' иішй бізнес, чи краще їх поставити в банк під відсотки і нічого не робити.
Задача 8. Нехай для ведения деякого бізнесу потрібно вкласти сьогодні 20 000 грн, а бізнес протягом п'яти місяців ще даватиме по 5000 грн доходу (ренты) наприкінці місяця. Депозитна ставка банку 1%. Чи варто займатися цим бізнесом?
=ПС(1%; 5; 5000). Відповідь: -24 267, 16 грн.
Висновок: вартість бізнесу (гранично допустима інвестиція) — 24 267 грн. Оскільки цю суму потрібно вкладати, отримали від'ємне число. Бізнес вигідний, бо для його ведения потрібно лише 20 000 грн. Чистий прибуток вигода становитиме не 5 000 грн, а 4 267 грн. Якби потрібно було більше, иіж 24 267 грн, то такий бізнес був би збитковим.
Задача 9. Умова та ж, що й в задачі 8, але рента (дохід) 21000 грн буде отримана наприкінці терміну. Чи вигідний такий бізнес?
=ПС(1%; 5;; 21000). Відповідь: -19 980,78.
Висновок: сьогоднішня вартість ренти 19 981 грн (отримали від'ємне число). Такий бізнес вигідним вважати не можна. Причина - немає змоги реінвестувати ренту. Краще покласти 20 000 грн в банк і нічого не робити.
Розглянемо функцію ЧПС (ДПС;рента1; рента2;...), яка обчислює сьогоднішню вартість різних рент що надходять на прикінці рівномірних періодів (англ.: NPV).
Задача 10. У бізнес потрібно вкласти сьогодні 27 000 грн. Наприкінці першого місяця потрібно вкласти ще 2000 грн., а в наступні п'ятъ місяців бізнес даватиме такі доходи: 4 000, 5 000, 6 000, 7 000, 8 000 грн. Чи цей бізнес вигідний?
=ЧПС(1%; 2000; 4000; 5000; 6000; 7000; 8000)
Відповідь: вартість бізнесу 26 756,44 грн. Оскільки затрати 27 000 грн більші за вартість бізнесу, то такий бізнес невигідний.
Задача 11. Вы маете сьогодні вкласти у бізнес 30 000 грн і будете вести його протягом п'яти місяців. Методом проб побудувати фінансову модель вигідного бізнесу.
Нехай щомісяця очікується такий дохід: 5000, 6000, 7000, 8000, 9000 — всього 35000. Оціни






