Виведення формули для знаходження площі поверхні зрізаного конуса

Площа поверхні циліндра, конуса, зрізаного конуса, кулі та її частин.

План.

 

1. Площа поверхні циліндра.

2. Площа поверхні конуса.

3. Площа поверхні зрізаного конуса.

4. Площа поверхні кулі.

5. Площа поверхні частин кулі.

 

 

Рекомендована література.

 

Математика: Підручник / О.М.Афанасьєва, Я.С.Бродський, О.Л.Павлов, А.К. Сліпенко. – К.: Вища шк., 2001. 447с.

Розділ 8.§ 2.п 2.4.

 

 

Дайте письмові відповіді на запитання.

Запишіть формули бічної та повної:

1. Площі поверхні циліндра.

2. Площі поверхні конуса.

3. Площі поверхні зрізаного конуса.

4. Площа поверхні кулі.

5. Площа поверхні частин кулі.

 

Площа поверхні циліндра

Поверхня циліндра складається з двох рівних основ і бічної поверхні. Якщо поверхню циліндра розрізати по колах основ і якій-небудь твір­ній, а потім розгорнути на площині, то дістанемо розгортку циліндра (рис. 1). Вона складається з прямокутника, сторони якого дорівнюють довжині кола основи циліндра і його висоті, і двох кругів, що дорівню­ють основам циліндра.

Площею бічної і повної поверхні циліндра називають площу розгортки бічної і повної поверхні. Тоді площа бічної поверхні S_біч і пло­ща повної поверхні S_цил визначаються формулами:

S_біч = 2πRH,

S_цил = 2πRH + 2πR ² = 2πR(H + R), де R, Н — радіус і висота циліндра відповідно.

Площа поверхні конуса

Бічну поверхню конуса, як і бічну поверхню циліндра, можна розгор­нути на площину, розрізавши її по твірній (рис. 170).

Розгорткою бічної поверхні конуса є круговий сектор, радіус якого Дорівнює твірній конуса, а довжина дуги сектора — довжині кола осно­ва конуса. Площею бічної поверхні конуса будемо вважати площу її розгортки. Виразимо площу бічної поверхні конуса S_біч, через його твірну l і радіус основи R. Площа кругового сектора — розгортки бічної поверхні конуса (рис. 170) — дорівнює , де α — градусна міра дуги АА₁, тому (1). Виразимо α через l і R. Оскільки довжина дуги АА₁ дорівнює 2πR (довжині кола основи конуса), то 2πR = , звідси . Підставивши цей вираз у формулу (1), одержимо: .

Рис. 170

Таким чином, площа бічної поверхні конуса дорівнює добутку поло­вини довжини кола основи та твірну: S_біч = πR l.

Площею повної поверхні конуса називається сума площ бічної пове­рхні та основи. Для обчислення площі повної поверхні конуса S_к одер­жуємо формулу

S_к = πR (l + R).

Виведення формули для знаходження площі поверхні зрізаного конуса

Виразимо площу S_біч бічної поверхні зрізаного конуса через його твірну l та радіуси r і R основ (R > r). Нехай точка S — вершина конуса, із якого одержано зрізаний конус, АА₁ — одна із твірних зрізаного ко­нуса, точки О і О₁ — центри основ (рис. 173). Використовуючи формулу S = πrl для знаходження бічної поверхні конуса, маємо:

S _біч = πR · AS – π r ·AS₁ = πR(SА ₁ + А ₁ А) – π r·А₁S₁.

Звідси, враховуючи, що АА₁ = l, знайдемо

S _біч = πR l + π(R – r)SA₁.

Виразимо SA₁ через l, R, r. Прямокутні трикутники SО₁А₁ і SOA подібні, оскільки мають спільний гострий кут S, тому

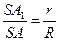, або . Звідси маємо: SA₁ = ; тоді

S_біч = πR l + π(R – r) · = πRl + πr l = π(r + R) l.

Отже, площа бічної поверхні зрізаного конуса дорівнює добутку півсуми довжин кіл основ на твірну конуса:

S _біч = π(r + R)l.

S_зр.к = S _біч + πr² + πR² = π(r + R)l + πr² + πR² — площа повної поверх­ні зрізаного конуса.

Площа сфери

Задача № 1

Навколо сфери радіуса r описано опуклий многогранник. Доведіть, що його об'єм V може бути обчислений за формулою

V = Sr, де S — площа поверхні многогранника.

Розв'язання

З'єднаємо центр сфери точку О з усіма вершинами многогранника (рис. 179). Тоді об'єм V многогранника дорівнює сумі об'ємів пірамід, основи яких — грані даного многогранника, а висота дорівнює радіусу г вписаної кулі:

V = S₁r + S₂r + S₃r +... + S_nr = r (S₁ + S₂ +...S_n) = rS,

де S₁, S₂, S₃ ,..., S_n — площі граней многогранника, S — площа поверхні многогранника.

Задача № 2

Радіус сфери дорівнює r. Знайдіть площу сфери.

Розв'язання

Опишемо навколо сфери опуклий многогранник з п малими граня­ми. Будемо необмежене збільшувати п таким чином, щоб площа кожної грані наближалася до нуля. За площу сфери приймемо границю послідо­вності площ поверхонь, описаних навколо сфери многогранників, за умови наближення до нуля площі кожної грані.

Нехай S_n — площа поверхні многогранника, V_n — його об'єм. Тоді, згідно з задачею № 1, маємо: V_n = S R.

Будемо тепер необмежене збільшувати число п, тоді число граней мно­гогранника буде необмежене збільшуватися, площа його поверхні буде на­ближатися до площі сфери S, а об'єм многогранника — до об'єму V кулі:

Отже V = SR, звідси маємо: S = = = 4πR².