Метод векторных диаграмм позволяет легко и быстро складывать токи и напряжения, выраженные синусоидальными функциями, но точность этого метода, как и любого графического, невелика. Кроме того, метод векторных диаграмм не позволяет выполнять операции умножения и деления. Поэтому наибольшее распространение в теории цепей получил метод, основанный на теории комплексных чисел.
Рассмотрим комплексную плоскость (рис. 4.10).
Положительную часть действительной оси обозначим +1, мнимой оси + j. В математике мнимую единицу обозначают i, в теории электрических цепей j, чтобы не путать с обозначением мгновенного значения тока (i).
Возьмем на комплексной плоскости точку 
с координатами а и b. Каждой точке комплексной плоскости можно поставить в соответствие вектор длиной А, расположенный под углом ψ к действительной оси. Поскольку любую синусоидальную величину можно представить вектором длиной А с углом наклона ψ, то этой синусоидальной величине можно поставить в соответствие точку на комплексной плоскости.
Комплексное число можно представить в трех формах записи.
1. Алгебраическая форма позволяет выразить комплексное число через координаты точки.
.
2. Тригонометрическая форма. Из треугольника 0 Аа видно, что 
, а 
, тогда комплексное число можно записать в виде
.
3. Показательная форма. Воспользуемся формулой Эйлера, связывающей тригонометрические функции с показательными:
,
тогда комплексное число можно записать в виде
.
А – модуль комплексного числа, который характеризует длину вектора;
ψ – аргумент комплексного числа, который характеризует угол поворота вектора относительно действительной оси.
Комплексные числа можно складывать, вычитать, делить и умножать. Как правило, сложение и вычитание производятся в алгебраической форме, а умножение и деление в показательной. Переход от одной формы к другой осуществляется по следующим правилам.
Если известны координаты точки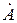 
, то модуль комплексного числа А можно найти по теореме Пифагора:
.
Аргумент находим из треугольника 0 Аа:
.
Поскольку угол ψ может принимать значения от 0 до 360о, то при его определении следует учитывать знаки действительной и мнимой частей:
при 
;
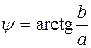при 
;
при 
;
при 
.
Переход от показательной формы к алгебраической осуществляется через тригонометрическую форму, то есть выражаем экспоненту по формуле Эйлера и находим , а .
При расчете комплексных чисел следует помнить следующие правила:
; 
; 
.
Это следует из выражения
, так как 
, то 
.
Две комплексные величины, имеющие равные модули и одинаковые по величине, но противоположные по знаку аргументы, называются комплексно- сопряженными.
Если комплексное число , то сопряженное ему число записывается в виде 
.
В алгебраической форме записи , сопряженное 
.
Произведение комплексного и сопряженного чисел равно квадрату модуля комплексного числа:
.
