Линейный интеграл векторного поля – это криволинейный интеграл второго рода. Вводится он следующим образом. Пусть в области G задано векторное поле 
, и в этом поле определена гладкая или кусочно-гладкая ориентированная кривая АВ. Разобьём кривую АВ на n частей точками деления 
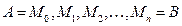по направлению от А к В. Радиус-вектор точки 
обозначим 
. Вектор 
. Выберем произвольно на каждой частичной дуге 
точку 
и вычислим значение поля 
в них. Для всех 
вычислим значения скалярного произведения 
и составим сумму вида 
.
Определение 6. Линейным интегралом векторного поля вдоль дуги АВ называется предел (если он существует), к которому стремится интегральная сумма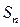 
, если наибольшая из длин частичных дуг 
стремится к нулю, а число элементарных дуг n неограниченно возрастает. Этот предел обозначают символом 
. Т.е.
. (5)
При изменении ориентации кривой интеграл меняет знак: 
.
Физический смысл выражения - это работа, произведённая силой при перемещении материальной точки от А к В по контуру L.
Линейный интеграл векторного поля вдоль замкнутой кривой (контура L) называется циркуляцией поля по замкнутому контуру при заданном направлении обхода контура и обозначается символом
Ц 
(6)
(знак + обозначает, что контур обходится против часовой стрелки).
Пусть поле задано своими функциями-координатами: 
и 
. Тогда
. (7)
В правой части выражения (7) - криволинейный интеграл второго рода.
Для плоского поля 
линейный интеграл вычисляется по формуле: 
. (8)
Линейный интеграл векторного поля вычисляется по обычным правилам вычисления криволинейного интеграла второго рода, т.е. преобразовывается в определённый. Для этого все переменные под знаком интеграла выражают через одну переменную, используя уравнение той линии, вдоль которой производится интегрирование.
Если векторное поле задано в пространстве 
, а линия АВ задана параметрическими уравнениями 
то
. (7.1)
Если линия АВ задана системой уравнений 
то
. (7.2)
Для плоского векторного поля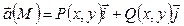 
и линии АВ, заданной параметрическими уравнениями 
, криволинейный интеграл вычисляется по формуле:
, (8.1)
где 
- значения параметра t, соответствующие начальной и конечной точкам пути интегрирования.
Для дуги АВ, заданной уравнением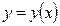 
: 
. (8.2)
Если линия АВ кусочно-гладкая, то следует воспользоваться свойством аддитивности криволинейного интеграла, разбив АВ на гладкие дуги.
Пример 10. Найти работу векторного поля 
при перемещении точки вдоль контура, состоящего из части кривой 
от точки 
до 
и дуги эллипса 
от точки до 
.
Решение.
Работа 
(см. (8)).
Т. к. контур состоит из двух частей, воспользуемся свойством аддитивности криволинейного интеграла: 
. Сведём оба интеграла к определённым по формулам (8.1) и (8.2). 
Для вычисления интеграла по контуру ВС используем параметрическую форму записи уравнения эллипса.
.
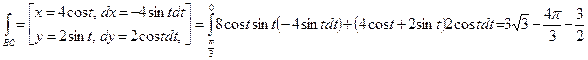Ответ: 
.
Пример 11. Вычислить циркуляцию векторного поля 
вдоль части кривой Вивиани, заданной пересечением полусферы 
и цилиндра 
, 
пробегаемой против часовой стрелки, если смотреть с положительной части оси OX.
Решение.
Воспользуемся формулой (7). Ц 
.
Чтобы свести подынтегральное выражение к одной переменной, перейдём в цилиндрическую систему координат: 
. Т.к. точка перемещается по кривой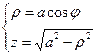 
, то считаем параметром полярный угол 
, 
, и получаем следующие параметрические уравнения этой кривой:
. Тогда 
.
Подставим полученные выражения в формулу для вычисления циркуляции:
Ц 
.
Учитывая свойства интегралов по симметричному интервалу от нечётных и чётных функций, получим: 
, и
Ц 
.
Ответ: Ц= 
.
Формула Грина.
Для плоского векторного поля 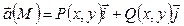имеет место следующее утверждение.
Если функции 
и их частные производные 
непрерывны в замкнутой области 
Г, где Г – граница односвязной области G, то
- формула Грина. (10)
обозначает положительное направление обхода (против часовой стрелки).
Пример 12. Используя формулу Грина, вычислить циркуляцию векторного поля 
по контуру, состоящему из отрезков OA, OB и большей дуги окружности 
, соединяющей точки A и B, если 
, 
, 
.
Решение.
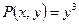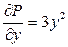По формуле Грина: Ц 
. 
, 
; 
, 
. Ц 
.
Проверим ответ, вычислив циркуляцию непосредственно по контуру с помощью линейного интеграла: Ц 
.
.
.
.
Ответ: Ц 
.
Контрольное задание 5.
Вычислить линейные интегралы векторного поля:
1) 
по ломаной 
.
2) 
по эллипсу а)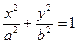 
, б) 
.
3) Вычислить циркуляцию векторного поля 
вдоль эллипса, полученного от пересечения цилиндра плоскостью 
в направлении по часовой стрелке, если смотреть из точки (0;10;0).
4) Вычислить линейный интеграл векторного поля 
вдоль ломаной линии ABOC, где 
, 
, 
, 
.
5) Найти работу поля 
вдоль части линии пересечения цилиндров 
и 
от точки 
через 
до точки 
.
