Пусть  - скалярное поле, заданное в области
- скалярное поле, заданное в области  .
.  - единичный фиксированный вектор. М – фиксированная точка,
- единичный фиксированный вектор. М – фиксированная точка,  .
.  - произвольная, отличная от М, точка из G, такая, что вектор
- произвольная, отличная от М, точка из G, такая, что вектор 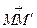 коллинеарен
коллинеарен  . Пусть
. Пусть  - величина направленного отрезка
- величина направленного отрезка  (равная
(равная  , если
, если 
 и равная -
и равная -  , если
, если 
 ).
).
Определение 2. Число  называется производной скалярного поля в направлении
называется производной скалярного поля в направлении  в точке М и обозначается символом
в точке М и обозначается символом  .
.
Производная скалярного поля в направлении  в точке М равна скорости изменения поля в этой точке в данном направлении. Если
в точке М равна скорости изменения поля в этой точке в данном направлении. Если  , то при перемещении из точки М в направлении
, то при перемещении из точки М в направлении  значение поля (функция
значение поля (функция 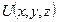 ) возрастает, если
) возрастает, если  - убывает.
- убывает.
Пусть поле  задано в декартовой системе координат и
задано в декартовой системе координат и  - единичный вектор данного направления. Тогда производная скалярного поля в направлении
- единичный вектор данного направления. Тогда производная скалярного поля в направлении  в точке M вычисляется по формуле:
в точке M вычисляется по формуле:  =
=  +
+ 
 ,где α,β,γ – углы, образуемые вектором
,где α,β,γ – углы, образуемые вектором  с соответствующими осями координат и
с соответствующими осями координат и  .
.
Если  , то
, то  ,
,  ,
,  ,
,
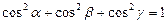
Для плоского поля  производная по направлению вычисляется по формуле:
производная по направлению вычисляется по формуле:  =
=  +
+  =
=  +
+  .
.
Пример 3. Установить характер изменения поля, заданного функцией  в точке
в точке  в направлении от А к точке
в направлении от А к точке  .
.
Решение. 
 ,
,  ,
,  .
.
Значения производных в точке А: 


 =
=  +
+ 


Ответ: Т.к.  поле убывает в направлении
поле убывает в направлении  .
.
Пример 4. Найти производную функции 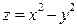 в точке
в точке  в направлении, составляющем угол
в направлении, составляющем угол  с положительным направлением оси ОХ.
с положительным направлением оси ОХ.
Решение. Для плоского поля  =
=  +
+  .
.
Значения производных в точке M:  ,
,  .
. 
 Ответ:
Ответ: 
Контрольное задание 2.
Найти производную функции:
1)  в точке
в точке 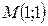 в направлении вектора
в направлении вектора  , составляющем угол
, составляющем угол  с положительным направлением оси ОХ;
с положительным направлением оси ОХ;
2)  в точке
в точке  в направлении вектора
в направлении вектора  , где
, где  ;
;
3)  в точке
в точке  в направлении вектора
в направлении вектора  ;
;
Градиент скалярного поля.
Определение 3. Градиентом скалярного поля  называется вектор-функция
называется вектор-функция  , (1)
, (1)
координатами которой являются соответствующие частные производные данной функции.
Если  - единичный вектор данного направления, то из формулы (1) следует, что производная по направлению
- единичный вектор данного направления, то из формулы (1) следует, что производная по направлению  - это скалярное произведение векторов
- это скалярное произведение векторов  и
и  ,т.е
,т.е 

 .
.
Но 
 =
= 
 . Тогда
. Тогда 

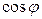 , т. к.
, т. к.  .
.
Здесь  - угол между вектором градиента в данной точке и вектором
- угол между вектором градиента в данной точке и вектором  .
.

 Отсюда следуют основные свойства градиента функции:
Отсюда следуют основные свойства градиента функции:
1. Вектор  в данной точке указывает направление наибольшего роста поля (функции
в данной точке указывает направление наибольшего роста поля (функции  ) в этой точке. При этом
) в этой точке. При этом 
 - наибольшее значение производной по направлению в точке M. (Таким образом, вектор
- наибольшее значение производной по направлению в точке M. (Таким образом, вектор  не зависит от выбора системы координат, а его модуль и направление в каждой точке определяются функцией
не зависит от выбора системы координат, а его модуль и направление в каждой точке определяются функцией  ).
).
2. Градиент скалярного поля в точке М ортогонален к поверхности (линии) уровня поля, проходящей через точку М.
3. Если  - поле постоянно, то его градиент равен 0.
- поле постоянно, то его градиент равен 0.
4. Справедливы формулы:
а)  ; б)
; б) 
в)  ; г)
; г) 
д)  , где U и V – скалярные поля.
, где U и V – скалярные поля.
е)  .
.
Пример 5. Найти градиент электростатического поля  , где е - заряд,
, где е - заряд, 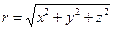 - расстояние от данной точки до заряда.
- расстояние от данной точки до заряда.
Решение. Данному полю принадлежат все точки пространства за исключением начала координат, где U обращается в бесконечность.
По определению:  . Вычислим частные производные:
. Вычислим частные производные:



 .
.
Ответ:  .
.
Пример 6. Найти наибольшую скорость возрастания функции  в точке
в точке  .
.
Решение. Направление наибольшего возрастания поля указывает вектор градиента этого поля.  .
.
Вычислим значения частных производных в точке M: 



Наибольшая скорость возрастания  равна наибольшему значению производной по направлению точке M
равна наибольшему значению производной по направлению точке M 

Ответ: Наибольшая скорость возрастания функции 
Контрольное задание 3.
1)Найти градиент скалярного поля  в точке
в точке  .
.
2) Найти наибольшую скорость возрастания поля  в точке
в точке  .
.
3) Найти производную функции  в точке
в точке  в направлении, перпендикулярном к линии уровня, проходящей через данную точку.
в направлении, перпендикулярном к линии уровня, проходящей через данную точку.
4) В каких точках градиент скалярного поля  :
:
а) параллелен оси OZ; б) перпендикулярен оси OZ; в) равен 0?
5) Найдите угол между градиентами скалярного поля  в точках
в точках  и
и 
Векторные линии поля.
Определение 4. Векторными линиями векторного поля  называются такие линии, у которых касательная в каждой точке направлена вдоль заданного в этой точке вектора поля.
называются такие линии, у которых касательная в каждой точке направлена вдоль заданного в этой точке вектора поля.
В физике это понятие для конкретных полей имеет физический смысл, например, векторные линии поля тяготения, электрического и магнитного полей - это силовые линии, а поля скоростей – линии тока, т.е. линии, по которым движутся частицы поля.
Пусть векторная линия, проходящая через точку  , описывается уравнениями
, описывается уравнениями  , где t – параметр. Из условия коллинеарности касательного вектора
, где t – параметр. Из условия коллинеарности касательного вектора  и вектора поля
и вектора поля 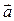 в произвольной точке дифференциальное уравнение этой линии имеет вид:
в произвольной точке дифференциальное уравнение этой линии имеет вид:  , (2)
, (2)
где λ – некоторое число.
Уравнение (2) - это дифференциальное уравнение векторных линий в векторной форме.
В пространстве  в декартовой системе координат:
в декартовой системе координат:  ,
,  . Тогда векторное уравнение (2) эквивалентно системе дифференциальных уравнений:
. Тогда векторное уравнение (2) эквивалентно системе дифференциальных уравнений:
 , (3)
, (3)
Система (3) – это симметричная форма системы дифференциальных уравнений. Для её решения применяются интегрируемые комбинации, с привлечением свойств равных дробей. Для плоского поля система имеет вид
 . (4)
. (4)
Определение 5. Поверхность, состоящая из векторных линий, проведённых через каждую точку некоторой замкнутой линии l, называется векторной трубкой.
В следующих примерах для данных векторных полей найдём уравнения векторных линий и построим их.
Пример 7. Векторное поле  .
.
Решение. Поле, у которого  , определено на всей плоскости XOY,следовательно, через каждую точку плоскости проходит хотя бы одна векторная линия. Составим дифференциальное уравнение векторных линий:
, определено на всей плоскости XOY,следовательно, через каждую точку плоскости проходит хотя бы одна векторная линия. Составим дифференциальное уравнение векторных линий:  (см. (4)). Это уравнение с разделяющимися переменными. Решим его:
(см. (4)). Это уравнение с разделяющимися переменными. Решим его:  , или
, или  - уравнения векторных линий. При С=0 это точка О(0,0), при С>0 – концентрические окружности.
- уравнения векторных линий. При С=0 это точка О(0,0), при С>0 – концентрические окружности.

 Для определения направления движения по векторной линии материальной точки, попавшей в векторное поле, рассмотрим проекцию вектора
Для определения направления движения по векторной линии материальной точки, попавшей в векторное поле, рассмотрим проекцию вектора  на ось OX. Это
на ось OX. Это  . Там, где
. Там, где  ,
,  составляет с осью OX острый угол, где
составляет с осью OX острый угол, где  - тупой. Учитывая, что вектор поля направлен по касательной к векторной линии, и векторные линии непрерывны, достаточно выяснить, что в первой четверти движение поля происходит по часовой стрелке (см.Рисунок 4).
- тупой. Учитывая, что вектор поля направлен по касательной к векторной линии, и векторные линии непрерывны, достаточно выяснить, что в первой четверти движение поля происходит по часовой стрелке (см.Рисунок 4).
Ответ:  - уравнения векторных линий.
- уравнения векторных линий.
Пример 8. Векторное поле  .
.
 Решение. Поле, у которого
Решение. Поле, у которого  , определено на всей плоскости XOY Составим дифференциальное уравнение векторных линий:
, определено на всей плоскости XOY Составим дифференциальное уравнение векторных линий:  . Решим его:
. Решим его: 
 . Рассмотрим случай
. Рассмотрим случай  . Тогда
. Тогда 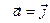 , т.е. ось OY тоже является векторной линией. Определим направление движения поля. Т.к.
, т.е. ось OY тоже является векторной линией. Определим направление движения поля. Т.к.  то вектор
то вектор  в любой точке составляет острый угол с осью OY (см.Рисунок 5).
в любой точке составляет острый угол с осью OY (см.Рисунок 5).
Ответ:  - уравнения векторных линий.
- уравнения векторных линий.
Пример 9. Найти векторные линии поля  .
.
Решение. Дифференциальные уравнения векторных линий:  (см. (3)). Из уравнения
(см. (3)). Из уравнения  следует
следует 
 - первый интеграл системы. Получили семейство плоскостей, проходящих через ось OY. Вторую интегрируемую комбинацию составим следующим образом.
- первый интеграл системы. Получили семейство плоскостей, проходящих через ось OY. Вторую интегрируемую комбинацию составим следующим образом.
Умножим числители и знаменатели системы соответственно на  :
:  .
.
Складывая, по свойству равных дробей получим: 


 , или
, или  - ещё один первый интеграл системы.
- ещё один первый интеграл системы.  - семейство сфер радиуса
- семейство сфер радиуса 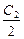 .
.
Ответ: векторные линии задаются системой (пересечением пар поверхностей): 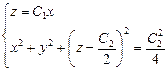
Контрольное задание 4.
Найти векторные линии поля:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 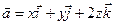 .
.






